| 这个作业属于哪个课程 | 班级链接 |
|---|---|
| 这个作业要求在哪里 | 作业要求链接 |
| 这个作业的目标 | 自动生成四则运算并计算答案 |
Team
3119005439 曾聿昊
PSP表格
| PSP | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 30 | 30 |
| · Estimate | · 估计这个任务需要多少时间 | 500 | 500 |
| Development | 开发 | 450 | 490 |
| · Analysis | · 需求分析 (包括学习新技术) | 120 | 150 |
| · Design Spec | · 生成设计文档 | 30 | 30 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 30 | 60 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 30 | 20 |
| · Design | · 具体设计 | 90 | 90 |
| · Coding | · 具体编码 | 120 | 120 |
| · Code Review | · 代码复审 | 30 | 20 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 20 | 20 |
| Reporting | 报告 | 30 | 30 |
| · Test Report | · 测试报告 | 30 | 30 |
| · Size Measurement | · 计算工作量 | 10 | 10 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 30 | 30 |
| 合计 | 600 | 640 |
具体实现
生成算式
一个算式由一个或多个运算符和多个运算数组成,需要生成算式,就需要考虑每个运算符左右都要有运算数。由此可以联想到二叉树结构,每个结点都可以存在最多两个子结点,我们可以类比根结点为运算符,两个子结点可以为运算符或运算数。如果此根结点的子结点也为一个运算符,则此子结点应该再生成两个对应的子结点,循环往复。直到你生成够了你想要的运算符数,则在剩余的结点都填入运算数即可生成一条正确的算式。
实现主要用Node类和My_Tree类:
class Node:
def __init__(selfs):
self.type = 0
self.operator = None
self.number = None
self.left = None
self.right = None
self.op_priority = {'+': 1, '-': 1, '*': 2, '/': 2}
class My_Tree:
def __init__(self):
self.root = Node()
self.op_list = ["+", "-", "*", "/"]
self.type = [1, 2]
self.middle_formula = list()
self.after_formula = list()
self.formula = list()
self.answer = list()
建树
def create(self, num_range, number):
num = 0
while num < number:
degree = random.choice([1, 2, 3])
empty_node = [self.root]
for _ in range(degree):
node = random.choice(empty_node)
empty_node.remove(node)
node.operator = random.choice(self.op_list)
node.type = 2
node.left = Node()
node.right = Node()
empty_node.append(node.left)
empty_node.append(node.right)
for node in empty_node:
node.type = 1
num_type = random.choice(self.type)
if num_type == 1:
node.number = random.randint(1, number)
else:
node.number = Fraction(random.randint(1, num_range), random.randint(1, num_range))
try:
self.root.get_answer()
self.middle_formula = self.root.get_formula()
self.after_formula = Convert.get_after_formula(self.middle_formula)
output = Convert.std_output(self.middle_formula)
if isinstance(self.root.number, Fraction):
answer = Convert.std_fraction(self.root.number)
else:
answer = self.root.number
if answer in self.answer:
continue
else:
self.formula.append(output)
self.answer.append(answer)
except NegativeError:
continue
except ZeroDivisionError:
continue
else:
num += 1
return self.formula, self.answer
运算优先级实现
小括号处理
小括号是用来解决运算时优先级的问题,由我们上面所述的二叉树算式生成来看,只要父母结点的运算符优先级大于等于我们的子结点的子树时,便在子树上添加小括号
def get_formula(self):
formula = list()
if self.type == 1:
return [self.number]
elif self.type == 2:
if self.left.type == 2 and
self.op_priority[str(self.operator)] > self.op_priority[str(self.left.operator)]:
formula.append('(')
formula += self.left.get_formula()
formula.append(')')
else:
formula += self.left.get_formula()
formula.append(self.operator)
if self.right.type == 2 and
self.op_priority[str(self.operator)] >= self.op_priority[str(self.right.operator)]:
formula.append('(')
formula += self.right.get_formula()
formula.append(')')
else:
formula += self.right.get_formula()
return formula
运算结果的计算
中缀表达式和后缀表达式的区别
中缀表达式就是我们常见的式子,如1+1,运算符在运算数中间表示,而后缀表达式则是运算符在运算数的后面,如1 1 +
中缀表达式更符合我们人的理解和计算,但是对于计算机的堆栈实现来说,后缀表达式则更符合计算机的执行顺序,效率也会更高。
中缀表达式转后缀表达式
因为最后计算需要用到后缀,所以我们要先把人理解的中缀变为计算机理解的后缀,这转变过程就称为逆波兰算法
我们用一个算式例子来了解一下什么是逆波兰算法:
2+3*4+(5*6+7)*8
我们需要判断运算符的优先级,如*的优先级比+高
接着我们需要用到两个栈,第一个栈存储运算符,第二个栈存储后缀表达式的结果
中缀表达式从左到右开始读取,遇到运算数直接存入第二个栈,此时第一个栈为空,第二个栈为2。
读取+,+号也入栈,因为只有+一个运算符,所以优先级肯定是最高的,此时第一个栈为+,第二个栈为2。
读取3,运算数直接入第二个栈,+,2 3
读取*,这个*比+的优先级高,所以*入栈,此时第一个栈为+ *,第二个栈为2 3
读取4,第一个栈为+ *,第二个栈为2 3 4
读取+,这个+号的优先级比目前第一个栈的栈顶*要低,所以弹出*到第二个栈中,然后第一个栈仅剩下+,与新碰到的+运算级相同,仍要弹出+,此时第一个栈为空,再把新遇到的+压入第一个栈。完成这步后,第一个栈为+,第二个栈为 2 3 4 * +
下面开始碰到左括号,左括号优先级高,不出栈,继续读入5。此时第一个栈为+ (,第二个栈为2 3 4 * + 5
读取*,因为在处理括号优先级的问题,所以先不输出左括号,直至碰到下一个右括号。此时第一个栈为+ ( *,第二个栈为 2 3 4 * + 5 6
读取+,优先级比*低,所以把*弹出,把+号压入第一个栈,再读入7,此时第一个栈为+ ( +,第二个栈为2 3 4 * + 5 6 * 7
开始碰到右括号,把栈中的括号弹出,但是左括号并不是栈顶,所以要先要把栈顶的+给弹出,左右括号不会真正输出到第二个栈,仅仅代表一种逻辑的关系。此时第一个栈为+,第二个栈为2 3 4 * + 5 6 * 7 +
继续读取*,优先级比+高,直接入第一个栈。
接着读取8,直接入第二个栈。
此时输入为空了,把第一个栈的运算符全部按顺序弹出到第二个栈作为最终的输出。所以第一个栈为空,第二个栈为2 3 4 * + 5 6 * 7 + 8 * +,第二个栈的结果就是最终计算机要计算的后缀表达式
代码如下
def get_after_formula(formula):
op_priority = {'(': 0, ')': 0, '+': 1, '-': 1, '*': 2, '/': 2}
postfix_formula = list()
op_list = list()
for item in formula:
if isinstance(item, int) or isinstance(item, Fraction):
postfix_formula.append(item)
elif item == '(':
op_list.append(item)
elif item == ')':
while op_list[-1] != '(':
postfix_formula.append(op_list.pop())
op_list.pop() #
else:
while len(op_list) > 0 and op_priority[op_list[-1]] >= op_priority[item]:
postfix_formula.append(op_list.pop())
op_list.append(item)
while op_list:
postfix_formula.append(op_list.pop())
return postfix_formula
计算后缀表达式
2+3*4+(5*6+7)*8,后缀表达式为2 3 4 * + 5 6 * 7 + 8 * +
2,3,4进栈,读到*,把两个操作数3和4弹出,计算得到12压回栈,此时栈为2,12。又读到+,弹出2和12,压回相加结果为14进栈。
5,6压入后,此时栈为14,5,6。读到*,计算5*6得到30压回栈,得到的栈为14,30。读到7,压入栈,得到14,30,7。
读到+,把30和7相加得37,压回栈,得到14,37。读到8,可以直接压入栈,得到14,37,8
读到*,把37*8的结果296压入栈,得到14,296
最后读到+,把14和296相加得到最终的结果310。
class Calculator:
def eval_expr(op_code, a, b):
answer = 0
if op_code == "+":
answer = operator.add(a, b)
elif op_code == "-":
if operator.lt(a, b):
raise NegativeError()
else:
answer = operator.sub(a, b)
elif op_code == "*":
answer = operator.mul(a, b)
elif op_code == "/":
if b == 0:
raise ZeroDivisionError
answer = operator.truediv(a, b)
if isinstance(answer, float): # if answer is float/double turn to Fraction
answer = operator.truediv(Fraction(a), Fraction(b))
return answer
异常处理
表达式的结果不能为负,定义一个异常类即可
class NegativeError(Exception):
def __init__(self):
super(NegativeError, self).__init__()
真分数的分母不能为0,对于这样的情况,直接用python的ZeroDivisionError异常类就可以。
性能分析
代码覆盖率
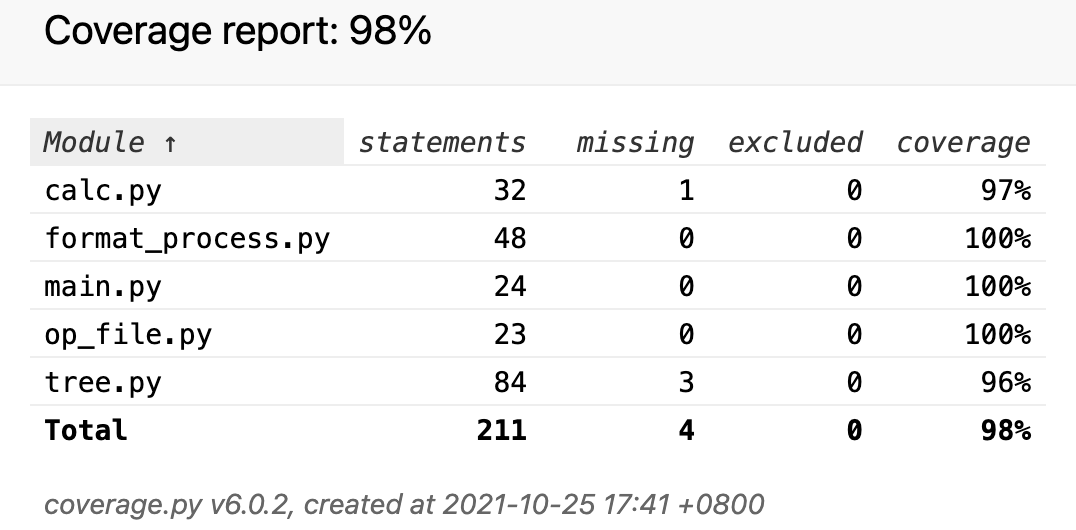
准确性测试
手工计算前2题,其他直接过,在Score.txt里看到的结果与预期一致