ABSTRACT
主要点为用MLP来替换传统CF算法中的内积操作来表示用户和物品之间的交互关系.
INTRODUCTION
NeuCF设计了一个基于神经网络结构的CF模型.文章使用的数据为隐式数据,想较于显性数据,implicit feedback更容易获取但比较难处理.文章的主要贡献有以下三点:
(1) 使用神经网络结构对用户以及物品的latent features进行建模,设计了一个通用的NCF框架.
(2) 文章证明了MF是NCF的一个特例,使用MLP赋予NCF获取高阶非线性交互的能力.
(3) 文章对两个真实数据集进行了大量实验,以证明我们的NCF方法的有效性以及深度学习协同过滤的前景。
PRELIMINARIES
隐式数据的描述参照DeepCF中implicit feedback的描述.目标函数的选择有以下两类:
(1) pointwise learning.使用回归框架来计算预测值$hat{y}_{ui}$以及真实值$y_{ui}$之间的误差.对于隐性反馈的处理,有两种方案:把所有未观测数据当作负样本;从未观测数据中进行负采样获取负样本.
(2) pairwise learning. pairwise核心思想是有用户对有观测的数据(产生过行为的数据)偏好度高与未观测数据.因此pariwise loss是最大化用户产生过行为的物品预测值$hat{y}_{ui}$以及用户没有产生过行为的物品的预测值$hat{y}_{uj}$.
使用神经网络来预测的NCF具备pointwise and pairwise learning的特性.
MF的详细介绍点这里,MF的主要局限性在于其使用线性的方法结合用户和物品的latent factor,下图举例论证了该观点:
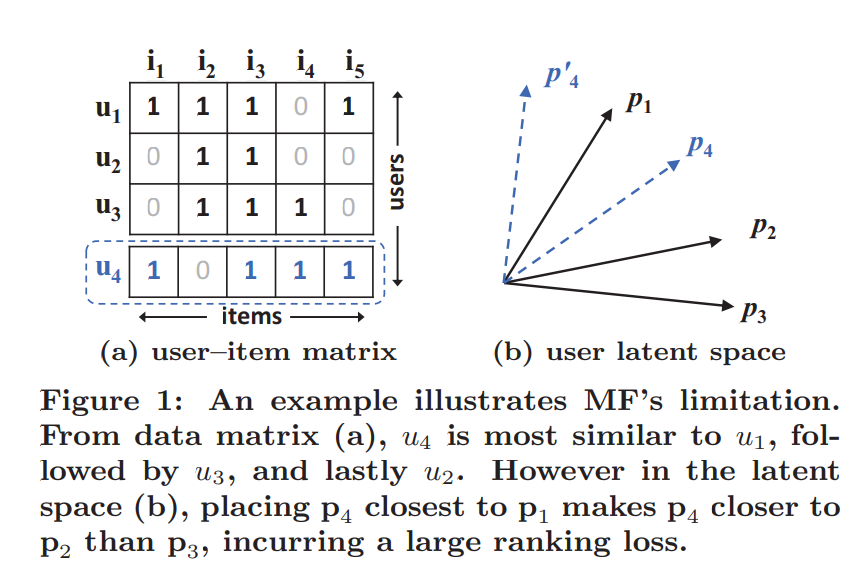
有学者尝试增加MF隐因的个数来提高其表达能力,这么做会影响MF的泛化能力.
NEURAL COLLABORATIVE FILTERING
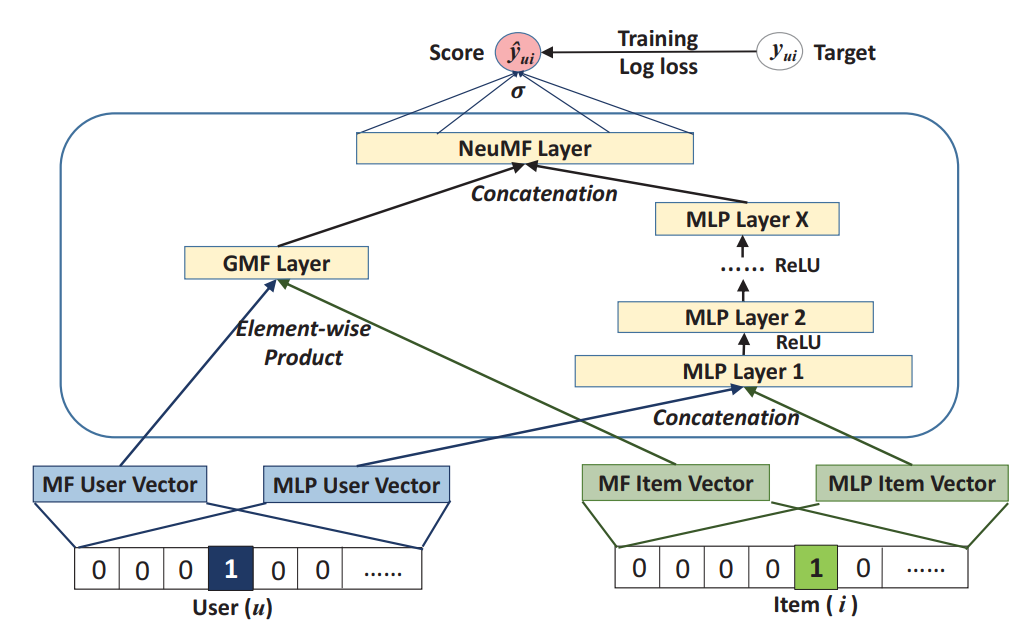
流程图如下所示:

文章仅考虑不考虑辅助信息的情况,对于后续可能产生的冷启动问题,可以通过添加辅助信息来解决. hidden layerX的维度决定了模型的容量,模型的预测公式如下:
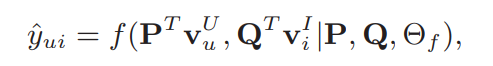
其中$PinRe^{M{ imes}K},QinRe^{N{ imes}K}$表示的是users以及items的latent factor,$ heta_f$为函数f的参数.
NCF学习问题 文章使用pointwise的方案来计算损失,对应的损失函数如下:

平方损失可以假设观测值是从高斯分布采样出来的,但这假设在implicit data不太行的通. 这里用一个概率的方式来描述这个implicit feedback,$y_{ui}$为用户u与物品i有关系的概率,在上述假设的前提下,模型的似然函数如下:
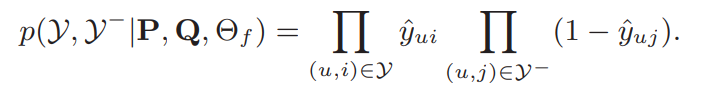
对应的损失函数如下所示:
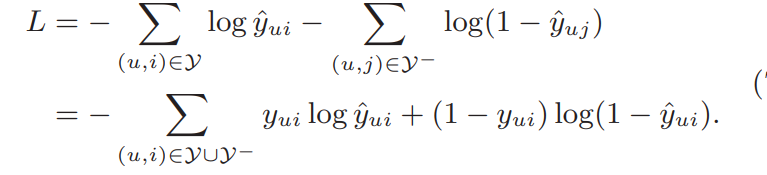
这部分的记号和DeepCF中的类似,处理的一个大致的思想也类似,不多说了.(这里负样本的获取是从未观测数据集合从采样而来,采样的比例是一个超参数)
GMF(Generalized Matrix Factorization)是MF在NCF的一个扩展,定义user latent vector $P_u$为${P^T}{V_{u}^{U}}$, item latent vector$q_i$为$Q^T{V_{i}^l}$
定义第一个neural CF layer为:
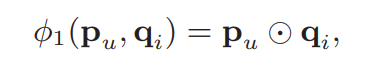
这里$odot$表示向量的追元素乘积(不是内积),输出层如下:
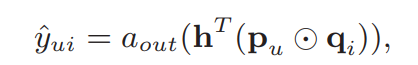
文章中设定$a_{out}$为sigmoid函数learns h from data with the log loss.当$a_{out},{h}$分别为激活函数以及输出层边的权重,当$a_out$为实体函数,$h$为值全为1的向量的时候,GMF就退化成朴素的MF.
MLP 结构的描述和DeepCF中类似,文章MLP的激活函数选择的是RELU主要考虑的是函数的饱和性问题,以及RELU激活函数比较适合稀疏的数据.(留个坑)在网络结构的设计上,文章遵循通用的塔形结构(输入层有较多神经元,从输入层到输出层神经元个数逐渐减少).这么做的前提是高层次的较少数的神经元能够从数据中学到较为抽象的数据.
GMF以及MLP的融合
GMF如果和MLP共享embedding layer的话会限制embedding layer的表达能力(两者对embedding layer起码size要求不一样).论文中GMF以及MLP有着独有的embedding layer.通过对两个模型最后的隐层级联来对两个模型进行融合,公式如下所示:
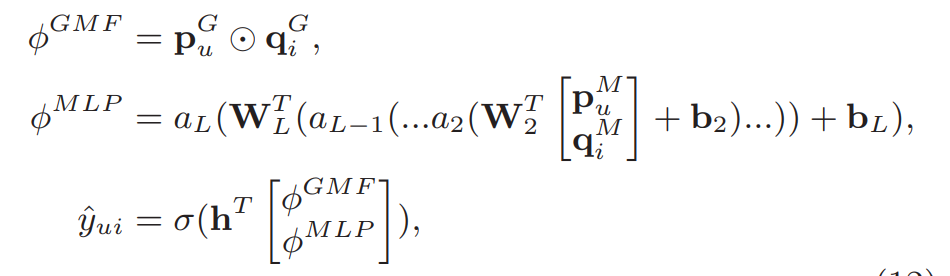
p,q对应user,item的latent factor.通过融合使得NeuCF即有GMF的线性表达能力也有MLP的非线性表达能力.模型的概念图如下所示: