zsm http://i.cnblogs.com/EditPosts.aspx?opt=1
摘要
人类所获得的信息大约70%来自于图像,数字图像处理是计算机对采样量化的图像进行去除噪声、增强、复原、分割、提前特征等处理的方法和技术,它对一个物体的数字表示施加一系列的操作,以得到所期望的结果。这种技术在航空航天、生物医学、通信工程、军事、文化、电子商务等方面应用广泛。本实验根据课堂所学的关于数字图像点运算的知识实现对数字图像的灰度直方图均衡处理和分段线性拉伸处理。
关键词
数字图像 点运算 灰度直方图 直方图均衡 分段线性拉伸
一、 任务说明
用Java编程语言实现一个带GUI的数字图像处理程序,实现读出数字图像并进行灰度直方图均衡处理和分段线性拉伸处理的功能。
需要注意的是,在本程序中,对于分段线性拉伸处理,程序中会先根据源图像的灰度直方图找出集中分布区间(像素个数之和占图像总像素个数85%以上的区间中长度最短的区间),然后让用户输入一个要拉伸到的区间,再进行分段线性拉伸。拉伸前后灰度范围都默认为 [0,255]。
二、 算法原理
(一)直方图均衡
1、 背景意义
直方图反映的是一幅图像的灰度级与出现这种灰度级概率之间关系的图形。直方图均衡的目的是使所有灰度级出现的相对概率相同,此时图像的熵最大,图像包含的信息最大。经过直方图均衡处理后,图像的对比度会增强,特别是对于背景或前景都太亮或太暗的图像非常有用。例如,其可以带来X光图像中更好的骨骼结构显示以及曝光过度或者曝光不足照片中更好的细节。
直方图均衡的主要优势是它是一个相当直观的技术并且是可逆操作,如果已知均衡化函数,那么就可以恢复原始的直方图,并且计算量也不大。这种方法的一个缺点是它对处理的数据不加选择,它可能会增加背景噪声的对比度并且降低有用信号的对比度。
2、 基本算法
若灰度级概率分布函数为 ,则此时直方图均衡的变换函数 s=T[r] 应该满足如下条件:
(a) T[r]为单值单调递增函数
(b) 0<T[r]<1,保证变换后像素灰度级仍在允许范围内
由转换原理可求得
则原灰度值 r 经变换后对应的新灰度值为
3、 扩展算法
上述基本算法是对于灰度级连续的情况而言的,而在计算机中图像的灰度级是离散的,实际上与连续情况类似,我们可以得到离散情况下的变换函数:
假定离散情况下共有L个灰度级,第k个灰度级出现的像素个数为,图像的总像素个数为N,则第k个灰度级出现的概率为:
从而均衡化的变换函数为:
则原灰度值r对应的新灰度值为
因此通过转换原图像每个像素的灰度值就可实现直方图均衡处理。
(二)分段线性拉伸
1、 背景意义
一般成像系统只具有一定的亮度响应范围,亮度的最大值与最小值之比称为对比度。由于成像系统的限制,常常出现对比度不足的问题,使人眼观看图像时的视觉效果较差,可以采用灰度变换(灰度修正)方法提高图像的对比度,增强图像。常用的灰度修正方法有:
(1) 线性变换
(2) 分段线性变换
(3) 非线性变换,如指数变换、对数变换等
这里采用的是 分段线性变换。
2、 基本算法
为了突出感兴趣的目标或灰度区间,相对抑制不感兴趣的灰度区间,可以采用分段线性变换。常用三段线性变换方法。
设原灰度直方图的灰度级的分布范围为[0,],集中分布在[a,b],又设变换后的直方图灰度级的分布范围为[0,],集中分布在[c,d],则变换公式如下:
对 :
对 :
对 :
3、 扩展算法
在本实验中,和都当成255,而原灰度级的集中分布范围 [a,b] 是通过程序算出来的,即从原图像的灰度直方图中找出一个连续灰度区间 [a,b] ,这个区间满足两个条件:
(1) 在此灰度级区间内的像素个数和占总像素个数的85%以上
(2) 此区间是满足(1)的区间中区间长度最短的
注:上述比例85%是在程序中默认的,其实应该做成能让用户自己输入一个比例,然后程序找出这个比例下灰度级的集中分布区间,但由于时间有限,程序中只默认为85%,没有实现让用户输入比例的功能。
三、 算法实现
功能函数:功能说明,输入参数说明,输出参数说明,算法流程(代码或伪代码,注释)
(一) 使用语言
本程序采用Java语言编写,开发平台为Eclipse (Version: Juno)
(二) 编译环境
java version "1.7.0_25"
Java(TM) SE Runtime Environment (build 1.7.0_25-b17)
(三) 功能函数
1、private BufferedImage getGrayPicture(BufferedImage originalImage)
(1) 功能说明:此函数获得输入图像的灰度图像,以及对应的灰度分布
(2) 输入参数说明:originalImage为输入的图像,类型为BufferedImage
(3) 输出参数说明:调用此函数后得到输入图像对应的灰度图像,并把个灰度级的像素个数存入全局数组huidunum[]中,供后面处理之用
(4) 算法流程:
遍历每个像素——>
获得该像素RGB值——>
获得R、G、B分量——>
得到灰度值——>
以灰度值为新R、G、B分量,得到新RGB值——>
新像素
// 获得图像的灰度图,并得到该图像个灰度级的像素个数 huidunum[]
private BufferedImage getGrayPicture(BufferedImage originalImage) {
int rgb, gray, alph, red, green, blue;
int imgwidth = originalImage.getWidth();
int imgheight = originalImage.getHeight();
BufferedImage huiduimg = new BufferedImage(imgwidth, imgheight,
originalImage.getType());// 不在原图像上修改,而是创建同样大小的一张图片
for (int i = 0; i < 256; i++)
huidunum[i] = 0; // 灰度分布初始化为0,即各灰度值像素个数初始化为0
for (int i = 0; i < imgwidth; i++) {
for (int j = 0; j < imgheight; j++) {// 遍历图像所以像素
rgb = originalImage.getRGB(i, j);// 获得该像素的rgb值,为一个4字节的整数,从高到低各字节值
// 分别表示
// 透明度appha、red、green、blue
alph = rgb >> 24; // 得到appha的值
red = (rgb & 0xff0000) >> 16;// 得到red值
green = (rgb & 0xff00) >> 8;// 得到green值
blue = (rgb & 0xff);// 得到blue值
gray = (int) (red * 299 + green * 587 + blue * 114) / 1000;// 根据公式由rgb三分量值得到灰度值gray
huidunum[gray]++;// 该灰度值像素个数加一
rgb = (alph << 24) | (gray << 16) | (gray << 8) | gray;// 由灰度值转rgb值,三分量都是gray值
huiduimg.setRGB(i, j, rgb);// 新rgb值
}
}
return huiduimg;
}
2、private BufferedImage hisEqual(BufferedImage originalImage)
(1) 功能说明:此函数实现直方图均衡化的功能
(2) 输入参数说明:originalImage为读入的图像
(3) 输出参数说明:获得对应的经过直方图均衡处理后的图像
(4) 算法流程:
遍历每个灰度值的像素个数huidunum[]——>
得到灰度值范围[0,当前灰度值]内的像素个数temp——>
该区间与总像素个数的比值——>
新灰度值=原灰度值×比值——>
以新灰度值为R、G、B分量得到RGB值——>
新像素
// 直方图均衡处理,不改变源图像
private BufferedImage hisEqual(BufferedImage originalImage) {
int alph, rgb, red, green, blue, gray;
int width = originalImage.getWidth();
int height = originalImage.getHeight();
double temp = 0.0;
BufferedImage transimg = new BufferedImage(width, height,
originalImage.getType());// 创建一张同样大小的新图片
for (int i = 0; i < 256; i++) {//遍历灰度直方图
temp = 0.0;
for (int j = 0; j <= i; j++) {//
temp = (double) huidunum[j] + temp;
}
temp = (temp / (double) width) / (double) height;
transhuidu[i] = (int) (255.0 * temp);
}
for (int i = 0; i < width; i++) {
for (int j = 0; j < height; j++) {
rgb = originalImage.getRGB(i, j);
alph = rgb >> 24;
red = (rgb & 0xff0000) >> 16;
green = (rgb & 0xff00) >> 8;
blue = (rgb & 0xff);
gray = (int) (red * 299 + green * 587 + blue * 114) / 1000;
gray = transhuidu[gray];// 新灰度值
rgb = (alph << 24)|(gray << 16)|(gray << 8) | gray;//新RGB值
transimg.setRGB(i, j, rgb);
}
}
return transimg;
}
3、private void getRecommendRange(int width, int height, int huidunum[])
(1) 功能说明:获得像素集中分布的灰度值范围
(2) 输入参数说明:三个参数分别为图像宽、高、各灰度值的像素个数
(3) 输出参数说明:函数得到像素集中分别的灰度值范围,下界、上界分别存入全局变量recommendstart、recommendend
(4) 算法流程:
初始化待求区间为[0,255]——>
以i遍历huidunum[]——>
以j遍历huidunum[i,255]——>
以k遍历huidunum[i,j] 并统计此区间内像素总个数sum——>
若sum不少于总像素个数的85%且区间[i,j]长度小于上次得到的区间长度,则取[i,j]。如此循环直到完。
// 获得源图像中占大部分的连续灰度值区间 [recommendstart,recommendend]
private void getRecommendRange(int width, int height, int huidunum[]) {
double sum = 0.0;
recommendstart = 0;
recommendend = 255;
for (int i = 0; i < 256; i++) {
for (int j = i; j < 256; j++) {
sum = 0.0;
for (int k = i; k <= j; k++) {
sum = sum + (double) huidunum[k];
}
if (sum > percentage * width * height) {
if (j - i < recommendend - recommendstart) {
recommendstart = i;
recommendend = j;
}
}
}
}
}
4、private int getNewGrayValue(int f, int a, int b, int c, int d)
(1) 功能说明:此函数实现灰度值转换
(2) 输入参数说明:f为原灰度值,[b,c]为原图像灰度值集中范围,[c,d]为要拉伸到的范围,由用户输入
(3) 输出参数说明:函数得到变换后的新灰度值
(4) 算法流程:此部分就是 二(二)2的编程实现,比较简单不再赘述
private int getNewGrayValue(int f, int a, int b, int c, int d) {
int newGrayValue = f;
if (f < a) {
newGrayValue = (int) ((double) c * (double) f / (double) a);
} else if (f > b) {
newGrayValue = (int) ((double) (f - b) * (double) (255 - d)
/ (double) (255 - b) + d);
} else {
newGrayValue = (int) ((double) (f - a) * (double) (d - c)
/ (double) (b - a) + c);
}
return newGrayValue;
}
5、 private BufferedImage Linearstretch(BufferedImage originalImage, int newgraystart, int newgrayend)
(1) 功能说明:根据用户输入的灰度值范围[newgraystart, newgrayend]进行分段线性拉伸
(2) 输入参数说明:originalImage为原图像,[newgraystart, newgrayend]为用户输入的灰度值范围
(3) 输出参数说明:函数执行成功后得到原图像经分段线性拉伸后的图像
(4) 算法流程:
执行getRecommendRange函数获得原图像计组像素集中分布的灰度值范围——>
遍历原图像的像素——>
获得该像素的rgb值——>
获得rgb值的分量r、g、b——>
获得灰度值gray——>
执行getNewGrayValue函数获得对应的新灰度值——>
以gray为三个分量获得新rgb值——>
得到新像素
private BufferedImage Linearstretch(BufferedImage originalImage,
int newgraystart, int newgrayend) {
int newhuidunum[] = new int[256];
int alph, rgb, red, green, blue, gray;
int width = originalImage.getWidth();
int height = originalImage.getHeight();
BufferedImage transimg = new BufferedImage(width, height,
originalImage.getType());
// 获得灰度大部分集中的范围 [recommendstart, recommendend]
getRecommendRange(width, height, huidunum);
for (int i = 0; i < width; i++) {
for (int j = 0; j < height; j++) {
rgb = originalImage.getRGB(i, j);
alph = rgb >> 24;
red = (rgb & 0xff0000) >> 16;
green = (rgb & 0xff00) >> 8;
blue = (rgb & 0xff);
gray = (int) (red * 299 + green * 587 + blue * 114) / 1000;
// 根据拉伸变换得到新的灰度值
gray = getNewGrayValue(gray, recommendstart, recommendend,
newgraystart, newgrayend);
rgb = (alph << 24) | (gray << 16) | (gray << 8) | gray;
transimg.setRGB(i, j, rgb);
newhuidunum[gray]++;
}
}
return transimg;
}
四、 实验
(一)灰度直方图均衡
- 1. 实验与结果

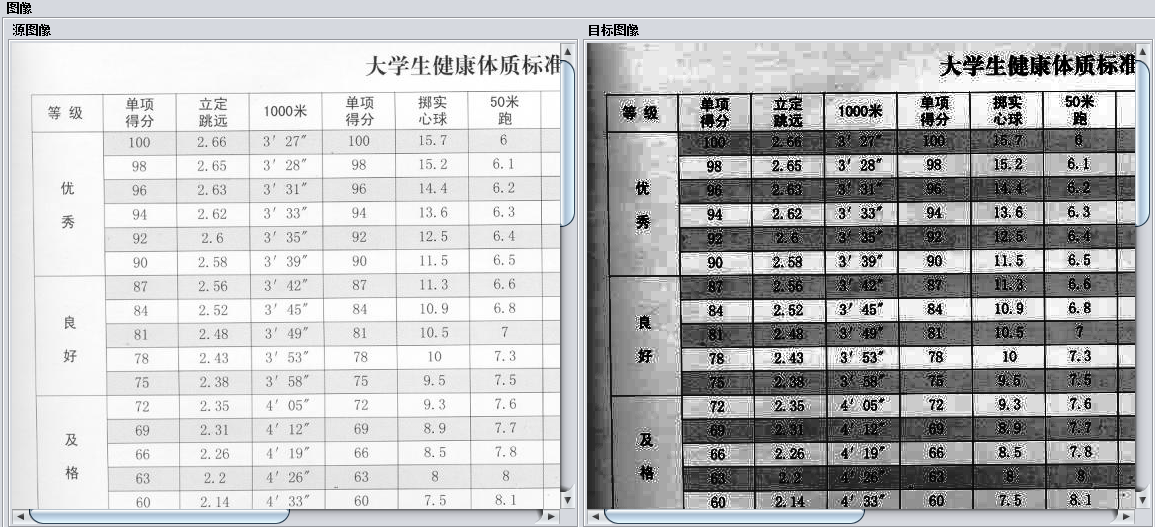
- 2. 结果分析
图像经过直方图均衡处理后,图像的对比度会增强,特别是对于背景或前景都太亮或太暗的图像非常有用。
均衡化后的各灰度级更加均衡,对于灰度范围小,直方图分布极不均匀的图像,可人为的适当的扩大灰度范围,均衡化后能取得较好的层次感,使图像信息变得更清晰。
(二)分段线性拉伸
(1)
实验与结果




(2) 结果分析
从以上实验及其结果对比可看出,线性变换可以把原图像相对较集中的灰度级拉伸到到指定的灰度级范围,当灰度级范围比原范围低时,图像将变暗,反之则变亮。
五、 结论
直方图均衡和线性拉伸是对数字图像进行处理的方法中的两种,是点运算。
直方图均衡处理可以使所有灰度级出现的相对概率相同,经过直方图均衡处理后,图像的对比度会增强,会更有层次感,特别是对于背景或前景都太亮或太暗的图像非常有用。
线性拉伸可以把原图像集中的灰度值区间拉伸到指定的区间上,这样可以突出感兴趣的目标或灰度区间,相对抑制不感兴趣的灰度区间。
参考文献
[1] 冈萨雷斯. 数字图像处理[M]. 北京:电子工业出版社, 2011.