啥是逻辑斯蒂回归呢
先别管那没多,它就一种分类方法:
我们先假设某个某个事件 E 发生的概率为p,那么该事件不发生的概率为1-p;
接下来,我们说下几率:一个事件发生的概率与它不发生的概率之比就是几率:即 P/1-P
那么我们知道如果事件E发生的概率越大,几率 P/1-P 越趋近于正无穷,否则趋近于0。
啥是对数几率呢,就是对几率P/1-P 取对数啊:ln(p/1-p)
那么我们知道如果事件E发生的概率越大,对数几率 ln(p/1-p) 越趋近于正无穷,否则趋近于负无穷.。
我们可以让 ln(p/1-p) 逼近一个线性函数 y= wx+b **************这个过程就是逻辑斯蒂回归了,也称对数几率回归
这时候 ln( p/ 1-p) 等价于 y= wx+b
问题来了,p等于多少:
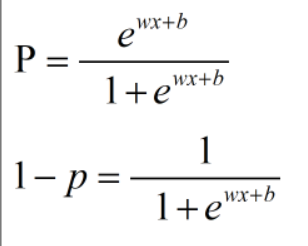
正好符合 ln( p/ 1-p) 等价于 y= wx+b
所以我们可以求出w和b ,来预测一个事件发生的概率p,同时 我们假定当p>=某个值a,就认为它会发生。
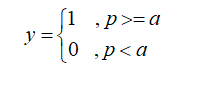
那么怎么算w和b两个参数呢?
既然是概率当然少不了似然估计法了
接下来是似然函数:
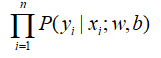 注意:这里的w是系数向量,
注意:这里的w是系数向量,![]() 是各特征变量所组成的向量
是各特征变量所组成的向量
第一步取对数:
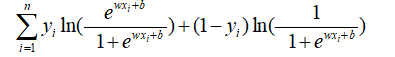
第二步整理下这个式子:
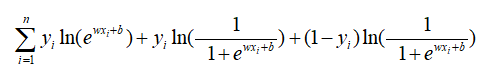
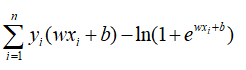 这是个凸函数,有最大值,我们要通过梯度下降求最小值,所以在该式前面加个负号,即对偶式
这是个凸函数,有最大值,我们要通过梯度下降求最小值,所以在该式前面加个负号,即对偶式  , 对此式梯度下降
, 对此式梯度下降
第三步梯度下降求解;
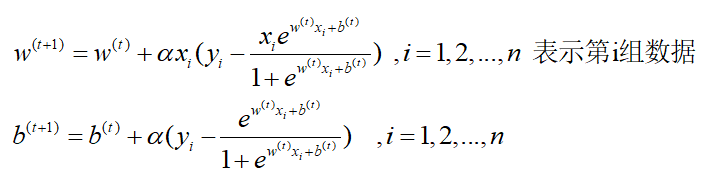
简化式子:

·················可能会出错,第一次推梯度下降,之前都没动过手,数学建模要用,临时推的。。。。