题目
Mathematicians are interesting (sometimes, I would say, even crazy) people. For example, my friend, a mathematician, thinks that it is very fun to play with a sequence of integer numbers. He writes the sequence in a row. If he wants he increases one number of the sequence, sometimes it is more interesting to decrease it (do you know why?..) And he likes to add the numbers in the interval [l;r]. But showing that he is really cool he adds only numbers which are equal some mod (modulo m).
Guess what he asked me, when he knew that I am a programmer? Yep, indeed, he asked me to write a program which could process these queries (n is the length of the sequence):
- + p r It increases the number with index p by r. (
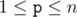 ,
, 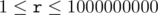 )
)
You have to output the number after the increase.
- - p r It decreases the number with index p by r. (
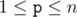 ,
, 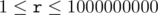 ) You must not decrease the number if it would become negative.
) You must not decrease the number if it would become negative.
You have to output the number after the decrease.
- s l r mod You have to output the sum of numbers in the interval
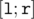 which are equal mod (modulo m). (
which are equal mod (modulo m). (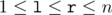 ) (
) (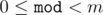 )
)
The first line of each test case contains the number of elements of the sequence n and the number m. (1 ≤ n ≤ 10000) (1 ≤ m ≤ 10)
The second line contains n initial numbers of the sequence. (0 ≤ number ≤ 1000000000)
The third line of each test case contains the number of queries q (1 ≤ q ≤ 10000).
The following q lines contains the queries (one query per line).
Output q lines - the answers to the queries.
题目大意
给你n和m以及n个数,q次操作,操作有三种:
在第p个数加r,输出现在的值
如果第p个数减r非负则将其减r,输出这个数
查询lr区间内模m余mod的数的和
分析
运用分块,因为m很小,我们可以记录每块中模m的各个可能值各种之和,同时维护每个数的值,修改是要将原来所在的分组减去原来数,再在新分组加上这个数。
代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<cctype>
#include<cmath>
#include<cstdlib>
#include<ctime>
#include<queue>
#include<vector>
#include<set>
#include<map>
#include<stack>
using namespace std;
long long n,m,sum,block,all[11000][20],beg[11000],a[11000],q,r[11000],l[11000];
inline long long read(){
long long x=0,f=1;char s=getchar();
while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
while(s>='0'&&s<='9'){x=(x<<3)+(x<<1)+(s-'0');s=getchar();}
return x*f;
}
inline void init(){
long long i,j,k;
block=sqrt(n);
sum=n%block==0?n/block:n/block+1;
for(i=1;i<=sum;i++)
l[i]=r[i-1]+1,r[i]=r[i-1]+block;
r[sum]=n;
for(i=1;i<=n;i++){
beg[i]=(i-1)/block+1;
all[beg[i]][a[i]%m]+=a[i];
}
}
inline void go(long long x,long long y){
if(a[x]+y<0){
printf("%I64d
",a[x]);
return;
}
all[beg[x]][a[x]%m]-=a[x];
a[x]+=y;
all[beg[x]][a[x]%m]+=a[x];
printf("%I64d
",a[x]);
}
inline void work(long long x,long long y,long long mod){
long long i,j,k,ans=0;
if(beg[x]==beg[y]){
for(i=x;i<=y;i++)
if(a[i]%m==mod)ans+=a[i];
}else {
for(i=x;i<=r[beg[x]];i++)
if(a[i]%m==mod)ans+=a[i];
for(i=beg[x]+1;i<beg[y];i++)
ans+=all[i][mod];
for(i=l[beg[y]];i<=y;i++)
if(a[i]%m==mod)ans+=a[i];
}
printf("%I64d
",ans);
return;
}
int main(){
long long i,j,k,x,y,mod;
n=read(),m=read();
for(i=1;i<=n;i++)a[i]=read();
init();
q=read();
for(i=1;i<=q;i++){
char c;
cin>>c;
if(c=='+'){
x=read(),y=read();
go(x,y);
}else if(c=='-'){
x=read(),y=read();
go(x,-y);
}else {
x=read(),y=read(),mod=read();
work(x,y,mod);
}
}
return 0;
}