题意: 对于Legend Tuple(下文称为LT)有以下3种规则:
1、(1,k)必然符合要求;
2、如果(n,k)符合要求,则(n+k,k)也符合要求;
3、如果(n,k)符合要求,则(n*k,k)也符合要求。
给出N、K,分别为n、k的范围,问有多少符合要求的LT。
思路:我们可以先看一下N==3,K==3时。
k=1:(1,1),(2,1),(3,1);
k=2: (1,2),(3,2),(2,2);
k=3: (1, 3),(3, 3) 共8种。
我们一开始都是把n固定为1,而k取[1,K]中的一个值,然后用第2、3规则取“扩散”出去找到别的。
这里我们就很明显是个bfs的思想了,但这题必不可能是bfs,不过不妨碍我们先打个表来看看。
//此处果断喊来队伍的工具人
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int n,k,ans=0;
bool vis[10005];
void bfs(int x)
{
memset(vis,false,sizeof(vis));
queue<int>q;
q.push(1);
vis[1]=true;
ans++;
while(!q.empty()){
int now=q.front();
int x1=now+x,x2=now*x;
if(x1<=n&&!vis[x1]){
q.push(x1);
vis[x1]=true;
ans++;
}
if(x2<=n&&!vis[x2]){
q.push(x2);
vis[x2]=true;
ans++;
}
q.pop();
}
}
int main()
{
int t;
cin>>t;
while(t--){
cin>>n>>k;
ans=0;
for(int i=1;i<=k;i++){
bfs(i);
}
cout<<ans<<endl;}
return 0;
}
得表:
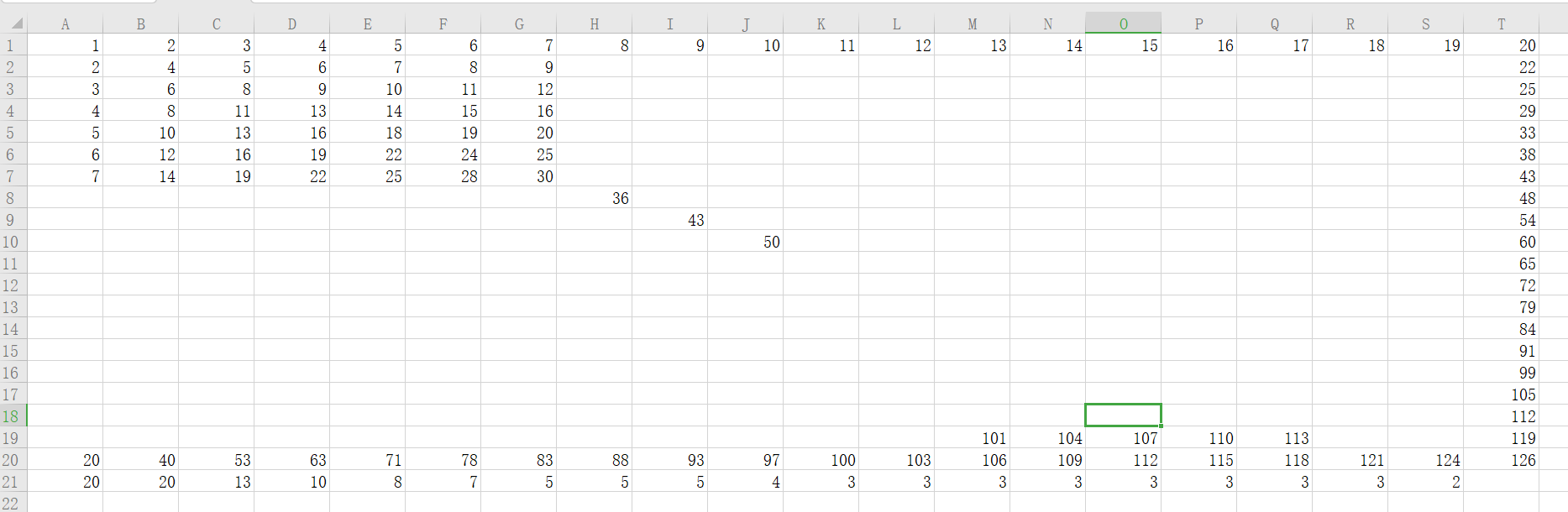
第21行是用第20行做的差。
当K>N时,对于任意的(1,i)/*i>N*/对于答案的贡献只有1。
当K<=N时,(1,i)/*i==N*/对于答案的贡献为2.
当K<N时,考虑i取不同值时对于答案的贡献。
i<=2,ans+=N;
2<i<=N,ans+=(n/i)*2+(i*i==N?0:1)/*原谅我不会打向上取整,嘤嘤嘤。。。*/
这里有个重点,也是这题为什么循环能AC的原因。我们不难看出在[3,N]这个区间上,有很多连续的区间,在这些区间上N/i是相同的。那么我们就可以跳着去累加,而不需要一个一个去看。
代码如下:
#include<bits/stdc++.h> using namespace std; #define ll long long ll mod=1e9+7; int main() { ll N,K; while(cin>>N>>K) { if(N==1){cout<<K%mod<<endl;continue;} ll ans=0; if(K>=N) { ans=(K-N)%mod; K=N-1; ans=(ans+2)%mod; } bool f=true; for(ll i=1; i<=K&&f; i++) { if(i<=2)ans=(ans+N)%mod; else { ll x=N/i;//x 6 i 3 if(x*i==N)ans=(ans+2*x)%mod; else { ll y=N/x;//3 if(y>K) { f=false; y=K; } if(y*x==N)y--; ans=(ans+ ((y-i+1)*x*2)%mod +(y-i+1)%mod )%mod; i=y; } } } cout<<ans<<endl; } return 0; }