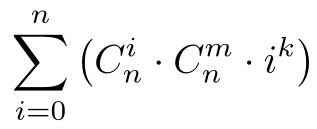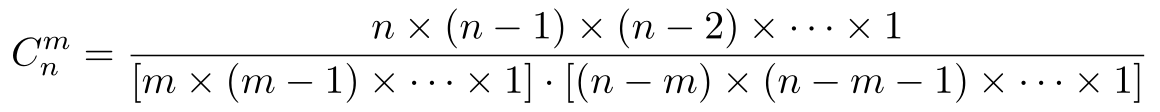1.结果填空 (满分12分)
2.结果填空 (满分15分)
3.结果填空 (满分10分)
4.程序设计(满分16分)
5.程序设计(满分20分)
6.程序设计(满分27分)
1.标题:填算式
请看下面的算式:
(ABCD - EFGH) * XY = 900
每个字母代表一个0~9的数字,不同字母代表不同数字,首位不能为0。
比如,(5012 - 4987) * 36 就是一个解。
请找到另一个解,并提交该解中 ABCD 所代表的整数。
请严格按照格式,通过浏览器提交答案。
注意:只提交 ABCD 所代表的整数,不要写其它附加内容,比如:说明性的文字。

6048
2.标题:骰子迷题
小明参加了少年宫的一项趣味活动:每个小朋友发给一个空白的骰子(它的6个面是空白的,没有数字),要小朋友自己设计每个面写哪个数字。但有如下要求:
1. 每个面只能填写 0 至 8 中的某一个数字。
2. 不同面可以填写同样的数字,但6个面总和必须等于24。
填好后,小朋友可以用自己填写好数字的骰子向少年宫的两个机器人挑战----玩掷骰子游戏。规则如下:
三方同时掷出自己的骰子,如果出现任何相同的数字,则三方都不计分。
如果三方数字都不同,则最小数字一方扣 1 分,最大数字一方加 1 分。
小明看到了两个机器人手中的骰子分别是:
0 0 0 8 8 8
1 1 4 5 6 7
请你替小明算一下,他如何填写,才能使自己得分的概率最大。
请提交小明应该填写的6个数字,按升序排列,数字间用一个空格分开。
如果认为有多个答案,提交字母序最小的那个方案。
请严格按照格式,通过浏览器提交答案。
注意:只提交一行内容,含有6个被空格分开的数字。不要写其它附加内容,比如:说明性的文字。

2 2 2 2 8 8
3.标题:埃及分数
古埃及曾经创造出灿烂的人类文明,他们的分数表示却很令人不解。古埃及喜欢把一个分数分解为类似: 1/a + 1/b 的格式。
这里,a 和 b 必须是不同的两个整数,分子必须为 1
比如,2/15 一共有 4 种不同的分解法(姑且称为埃及分解法):
1/8 + 1/120
1/9 + 1/45
1/10 + 1/30
1/12 + 1/20
那么, 2/45 一共有多少个不同的埃及分解呢(满足加法交换律的算同种分解)? 请直接提交该整数(千万不要提交详细的分解式!)。
请严格按照要求,通过浏览器提交答案。
注意:只提交分解的种类数,不要写其它附加内容,比如:说明性的文字

//7 import java.util.Scanner; public class Main { static Scanner sc = new Scanner(System.in); static int gcd(int a,int b) { if(b==0) return a; return gcd(b,a%b); } public static void main(String[] args){ for(int i=1;i<=10000;i++) { for(int j=i+1;j<=10000;j++) { int g=gcd(i+j,i*j); if((i+j)/g==2&&(i*j)/g==45) { System.out.println("1/"+i+"+1/"+j); } } } } }
4.标题:约数倍数选卡片
闲暇时,福尔摩斯和华生玩一个游戏:
在N张卡片上写有N个整数。两人轮流拿走一张卡片。要求下一个人拿的数字一定是前一个人拿的数字的约数或倍数。例如,某次福尔摩斯拿走的卡片上写着数字“6”,则接下来华生可以拿的数字包括:
1,2,3, 6,12,18,24 ....
当轮到某一方拿卡片时,没有满足要求的卡片可选,则该方为输方。
请你利用计算机的优势计算一下,在已知所有卡片上的数字和可选哪些数字的条件下,怎样选择才能保证必胜!
当选多个数字都可以必胜时,输出其中最小的数字。如果无论如何都会输,则输出-1。
输入数据为2行。第一行是若干空格分开的整数(每个整数介于1~100间),表示当前剩余的所有卡片。
第二行也是若干空格分开的整数,表示可以选的数字。当然,第二行的数字必须完全包含在第一行的数字中。
程序则输出必胜的招法!!
例如:
用户输入:
2 3 6
3 6
则程序应该输出:
3
再如:
用户输入:
1 2 2 3 3 4 5
3 4 5
则程序应该输出:
4
资源约定:
峰值内存消耗(含虚拟机) < 64M
CPU消耗 < 2000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.6及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。
5.标题:网络寻路
X 国的一个网络使用若干条线路连接若干个节点。节点间的通信是双向的。某重要数据包,为了安全起见,必须恰好被转发两次到达目的地。该包可能在任意一个节点产生,我们需要知道该网络中一共有多少种不同的转发路径。
源地址和目标地址可以相同,但中间节点必须不同。
如图1所示的网络。
1 -> 2 -> 3 -> 1 是允许的
1 -> 2 -> 1-> 2 或者 1->2->3->2 都是非法的。
输入数据的第一行为两个整数N M,分别表示节点个数和连接线路的条数(1<=N<=10000; 0<=M<=100000)。
接下去有M行,每行为两个整数 u 和 v,表示节点u 和 v 联通(1<=u,v<=N , u!=v)。
输入数据保证任意两点最多只有一条边连接,并且没有自己连自己的边,即不存在重边和自环。
输出一个整数,表示满足要求的路径条数。
例如:
用户输入:
3 3
1 2
2 3
1 3
则程序应该输出:
6
再例如:
用户输入:
4 4
1 2
2 3
3 1
1 4
则程序应该输出:
10
资源约定:
峰值内存消耗(含虚拟机) < 64M
CPU消耗 < 2000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.6及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。


import java.util.ArrayList; import java.util.Scanner; public class Main { static Scanner sc = new Scanner(System.in); static class Node{ ArrayList<Integer> v = new ArrayList<Integer>(); } static Node[] v = new Node[10005]; static long c; static void dfs(int pre,int x,int s) { if(s==3) { c+=v[x].v.size()-1; //剪枝 return; } for(int i=0;i<v[x].v.size();i++) { int to = v[x].v.get(i); if(to==pre) continue; dfs(x,to,s+1); } } public static void main(String[] args) { int n=sc.nextInt(); for(int i=1;i<=n;i++) { v[i] = new Node(); } int m=sc.nextInt(); int x,y; for(int i=1;i<=m;i++) { x=sc.nextInt(); y=sc.nextInt(); v[x].v.add(y); v[y].v.add(x); } c=0; for(int i=1;i<=n;i++) { dfs(-1,i,1); } System.out.println(c); } }
6.标题:公式求值
输入n, m, k,输出图1所示的公式的值。其中C_n^m是组合数,表示在n个人的集合中选出m个人组成一个集合的方案数。组合数的计算公式如图2所示。
输入的第一行包含一个整数n;第二行包含一个整数m,第三行包含一个整数k。
计算图1所示的公式的值,由于答案非常大,请输出这个值除以999101的余数。
【样例输入1】
3
1
3
【样例输出1】
162
【样例输入2】
20
10
10
【样例输出2】
359316
【数据规模与约定】
对于10%的数据,n≤10,k≤3;
对于20%的数据,n≤20,k≤3;
对于30%的数据,n≤1000,k≤5;
对于40%的数据,n≤10^7,k≤10;
对于60%的数据,n≤10^15,k ≤100;
对于70%的数据,n≤10^100,k≤200;
对于80%的数据,n≤10^500,k ≤500;
对于100%的数据,n在十进制下不超过1000位,即1≤n<10^1000,1≤k≤1000,同时0≤m≤n,k≤n。
【提示】
999101是一个质数;
当n位数比较多时,绝大多数情况下答案都是0,但评测的时候会选取一些答案不是0的数据;
资源约定:
峰值内存消耗(含虚拟机) < 128M
CPU消耗 < 2000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意:不要使用package语句。不要使用jdk1.6及以上版本的特性。
注意:主类的名字必须是:Main,否则按无效代码处理。