九宫重排
时间限制:1.0s 内存限制:256.0MB
问题描述
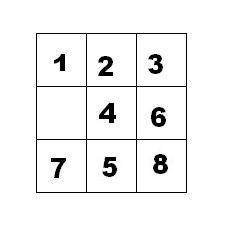
如下面第一个图的九宫格中,放着 1~8 的数字卡片,还有一个格子空着。与空格子相邻的格子中的卡片可以移动到空格中。经过若干次移动,可以形成第二个图所示的局面。
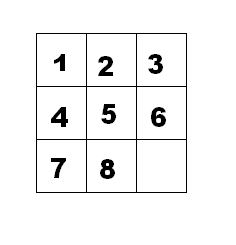
我们把第一个图的局面记为:12345678.
把第二个图的局面记为:123.46758
显然是按从上到下,从左到右的顺序记录数字,空格记为句点。
本题目的任务是已知九宫的初态和终态,求最少经过多少步的移动可以到达。如果无论多少步都无法到达,则输出-1。
我们把第一个图的局面记为:12345678.
把第二个图的局面记为:123.46758
显然是按从上到下,从左到右的顺序记录数字,空格记为句点。
本题目的任务是已知九宫的初态和终态,求最少经过多少步的移动可以到达。如果无论多少步都无法到达,则输出-1。
输入格式
输入第一行包含九宫的初态,第二行包含九宫的终态。
输出格式
输出最少的步数,如果不存在方案,则输出-1。
样例输入
12345678.
123.46758
123.46758
样例输出
3
样例输入
13524678.
46758123.
46758123.
样例输出
22
BFS。将字符串视作状态,将“.”视作位移点,每次向四个方向移动的同时交换字符。
很明显需要用到HashMap来记录状态,开始时图方便我把字符串转换成二维数组作为HashMap的键值,然后就遇到各种问题。。
首先二维数组作为键值记录的是地址而并非数组元素,所以即使是两个相同的数组代表的也是不同的键值。
其次用二维数组来进行操作效率极低。。
最终还是回到了字符串处理上,用一维来表示二维状态,仔细推敲后其实并不麻烦(详见代码)。
注意字符交换时replace用到的小技巧。
然后就是算法方面了,这道题用bfs显然是可做的:

import java.util.ArrayDeque; import java.util.HashMap; import java.util.Scanner; public class Main { static Scanner sc = new Scanner(System.in); static String beg,end; static int[][] t = {{1,0},{0,1},{-1,0},{0,-1}}; static HashMap<String,Integer> b = new HashMap<String,Integer>(); static class Node{ String a; int x,s; public Node(String a,int x,int s) { this.a=a; this.x=x; this.s=s; } } static ArrayDeque<Node> q = new ArrayDeque<Node>(); static int bfs(int bx,int ex) { b.put(end, -1); if(b.get(beg)!=null) return 0; b.put(beg, 0); q.offerLast(new Node(beg,bx,0)); while(q.size()>0) { String a=q.peekFirst().a; int x=q.peekFirst().x/3; int y=q.peekFirst().x%3; int s=q.peekFirst().s; q.pollFirst(); for(int i=0;i<4;i++) { int tx=x+t[i][0]; int ty=y+t[i][1]; if(tx<0||ty<0||tx>=3||ty>=3) continue; char tt=a.charAt(tx*3+ty); String ta=a; ta=ta.replace(tt, '!'); ta=ta.replace('.', tt); ta=ta.replace('!', '.'); if(b.get(ta)!=null){ if(b.get(ta)==-1) return s+1; continue; } b.put(ta, s+1); q.offerLast(new Node(ta,tx*3+ty,s+1)); } } return -1; } public static void main(String[] args) { beg = sc.next(); end = sc.next(); int bx=0,ex=0; for(int i=0;i<9;i++) { if(beg.charAt(i)=='.'){ bx=i; break; } } for(int i=0;i<9;i++) { if(end.charAt(i)=='.'){ ex=i; break; } } System.out.println(bfs(bx,ex)); } }
但官网提交显示只过了80%数据
因此需要想到使用双起点bfs优化,起点终点一起搜,大大减少了分支情况。
碰头时两边步数+当前1即为最终解。

import java.util.ArrayDeque; import java.util.HashMap; import java.util.Scanner; public class Main { static Scanner sc = new Scanner(System.in); static String beg,end; static int[][] t = {{1,0},{0,1},{-1,0},{0,-1}}; static HashMap<String,Integer> bb = new HashMap<String,Integer>(); static HashMap<String,Integer> be = new HashMap<String,Integer>(); static class Node{ String a; int x,s,m; public Node(String a,int x,int s,int m) { this.a=a; this.x=x; this.s=s; this.m=m; } } static ArrayDeque<Node> q = new ArrayDeque<Node>(); static int bfs(int bx,int ex) { if(beg.equals(end)) return 0; bb.put(beg, 0);be.put(end, 0); q.offerLast(new Node(beg,bx,0,1)); q.offerLast(new Node(end,ex,0,2)); while(q.size()>0) { String a=q.peekFirst().a; int x=q.peekFirst().x/3; int y=q.peekFirst().x%3; int s=q.peekFirst().s; int m=q.peekFirst().m; q.pollFirst(); for(int i=0;i<4;i++) { int tx=x+t[i][0]; int ty=y+t[i][1]; if(tx<0||ty<0||tx>=3||ty>=3) continue; char tt=a.charAt(tx*3+ty); String ta=a; ta=ta.replace(tt, '!'); ta=ta.replace('.', tt); ta=ta.replace('!', '.'); if(m==1){ if(bb.get(ta)!=null) continue; if(be.get(ta)!=null) return be.get(ta)+s+1; bb.put(ta, s+1); } else{ if(be.get(ta)!=null) continue; if(bb.get(ta)!=null) return bb.get(ta)+s+1; be.put(ta, s+1); } q.offerLast(new Node(ta,tx*3+ty,s+1,m)); } } return -1; } public static void main(String[] args) { beg = sc.next(); end = sc.next(); int bx=0,ex=0; for(int i=0;i<9;i++) { if(beg.charAt(i)=='.'){ bx=i; break; } } for(int i=0;i<9;i++) { if(end.charAt(i)=='.'){ ex=i; break; } } System.out.println(bfs(bx,ex)); } }
