1.Dp的初步(数学三角形问题)又称数塔问题是最基础dp入门问题

题意:求从顶层走到底层,若每一步只能走到相邻的结点,则经过的结点的数字之和最大是多少?
仔细读题思考之后很容易发现这个数塔存在 dp(i,j)=dp(i,j)+max(dp(i+1,j),dp(i+1,j+1));的关系
解法:其实很明显我们可以倒数第二层依次求取每一个节点的最大值,直到最顶端的节点,所以我们可以得到以下代码
for(int i=n-1;i>=1;i--){
for(int j=1;j<=i;j++){
dp(i,j)=dp(i,j)+max(dp(i+1,j),dp(i+1,j+1));
}
}
当然最下面的一层就等于它本身,经过计算之后我们就可以得到此数塔的从最顶层走到最低层的最大值dp[0][0];
接下来我们来看一个数塔的变形(说来惭愧当时自己在做的时候没有马上想到数塔)
HDU 1176免费馅饼

题意:就是天上会掉下许多馅饼,最开始时你在5号位置,你可以经过左右移动来吃吃到馅饼,一秒钟可以移动1个单位距离,如 他第一秒可以吃到4,5,6上的馅饼
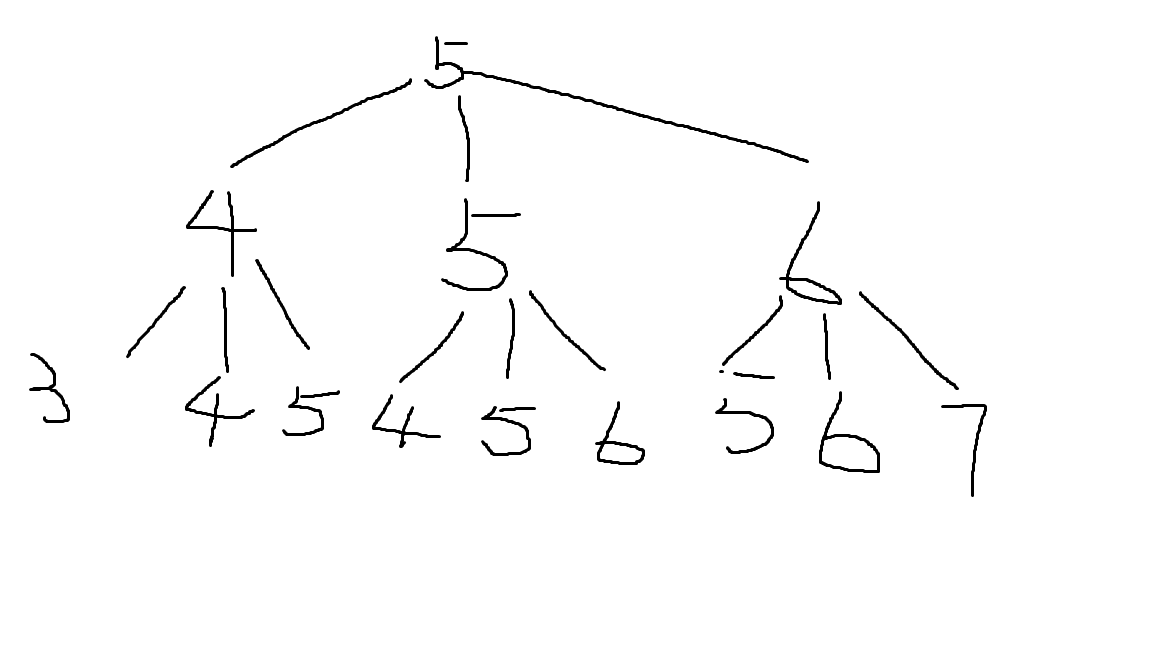
如图我们可以得到以上数塔
每一层表示一秒,节点数字表示当前位置
所以参考数塔的状态转移方程我们可以得到以下的状态转移方程
for (int i = tt-1; i>=0; i--) {
for (int j =10; j >=0; j--) {
dp[i][j] = max(dp[i+1][j], max(dp[i + 1][j-1], dp[i + 1][j + 1]))+dp[i][j]; //i代表秒数(表示层数),j代表位置
}
}