一、思维导图
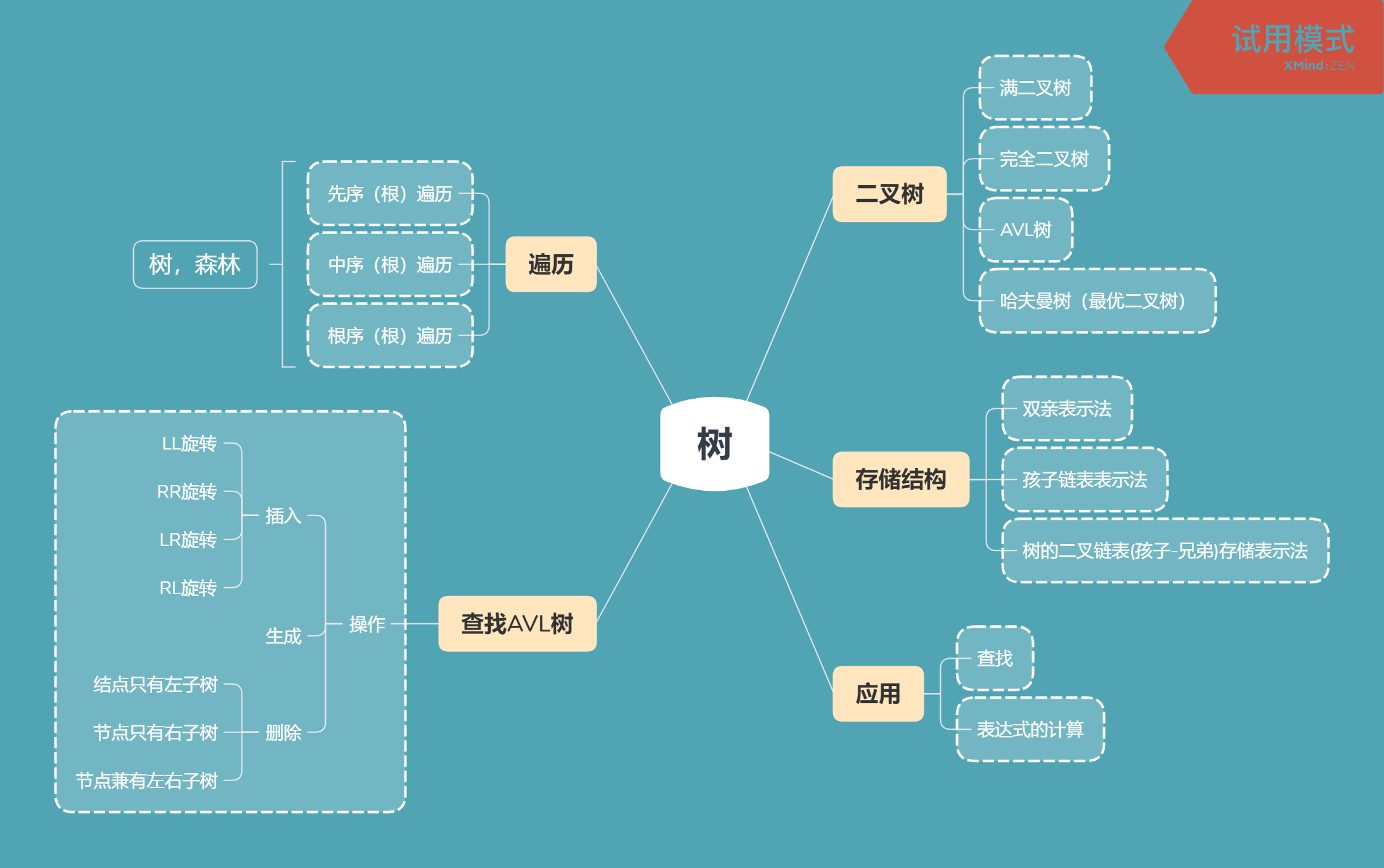
1.树
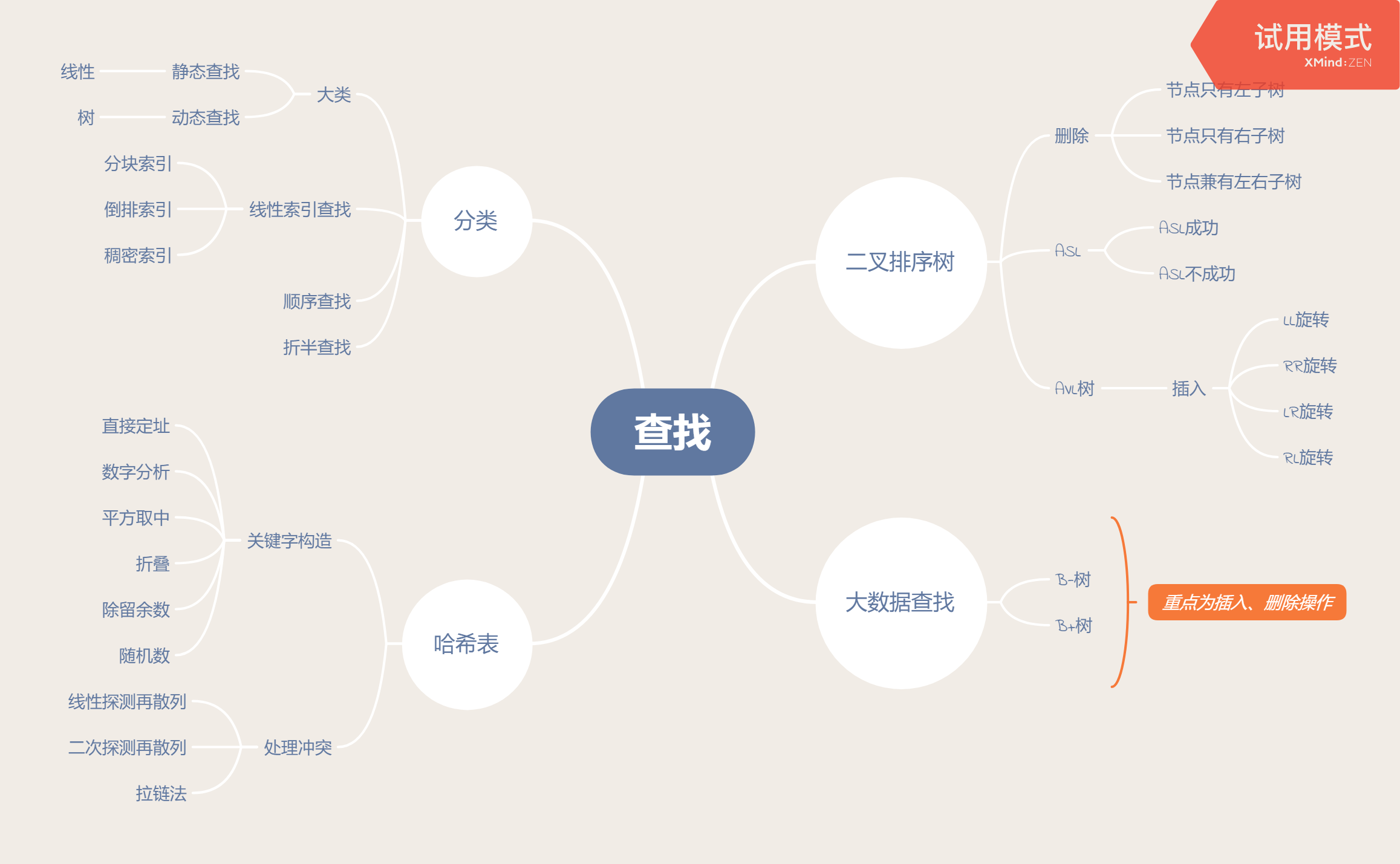
2.查找
二、树的基本知识
结点:指树中的一个元素;
结点的度:指结点拥有的子树的个数,二叉树的度不大于2。
数的度:指树中的最大结点度数。
叶子:度为0的结点,也称为终端结点。
高度:叶子节点的高度为1,根节点高度最高。
层:根在第一层,以此类推。
三、性质
1.二叉树的性质:
(1):
二叉树的第i层上至多有2^(i-1)个结点。
(2):
深度为k的二叉树,至多有2^k-1个结点。
满二叉树:叶子节点一定要在最后一层,并且所有非叶子节点都存在左孩子和右孩子。
最特别的二叉树:完全二叉树:从左到右、从上到下构建的二叉树。
(3):
非空二叉树上的叶子结点数等于度为2的结点数加1,即n0=n2+1。
2.完全二叉树的性质:
(1):
结点 i 的子结点为2i 和 2i+1(前提是都小于总结点数)。
(2):
结点 i 的父结点为 i/2。
三、线索二叉树
二叉树结点的各种遍历序列,其实质是对一个非线性结构进行线性化的操作,使这个访问序列中的每个结点(第一个和最后一个除外)都有一个直接前驱和直接后继。
传统的链式存储仅能体现一种父子关系,不能直接得到结点在遍历中的前驱和后继。引入线索二叉树是为了加快查找结点前驱和后继的速度。
在二叉树线索化时,通常规定:若无左子树,令lchild指向其前驱结点,若无右子树,令rchild指向其后继结点。还需要增加两个标志域表明当前指针域所指对象是指向左(右)子结点还是指向直接前驱(后继)。
四、二叉排序树
二叉排序树(BST),也称二叉查找树。它是一棵空树,或者满足:
(1)若左子树非空,左子树上所有结点关键字值均小于根结点
(2)若右子树非空,右子树上所有结点关键字值均大于根结点
(3)左、右子树也均为二叉排序树
二叉排序树是一个递归的数据结构。对二叉排序树进行中序遍历,可以得到一个递增的有序序列。
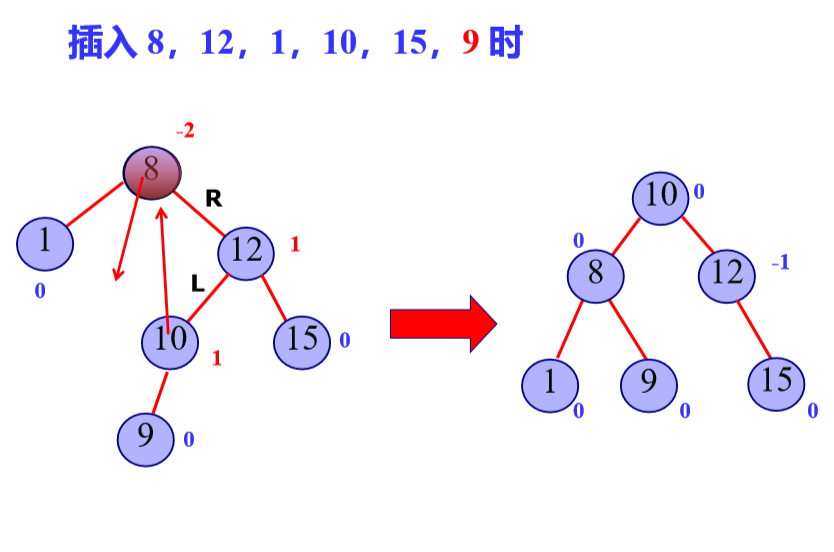
平衡二叉树(AVL),是为了避免树的高度增长过快,降低二叉排序树的性能。规定在插入和删除二叉树结点时,保证任意结点的左、右子树高度差的绝对值不超过1。
1插入
插入后判断是否有结点因此次操作不平衡。先找到插入路径上离插入结点最近的平衡因子绝对值大于1的结点A,再对以A为根的子树,在保持二叉排序树特性的前提下,调整各结点的关系。
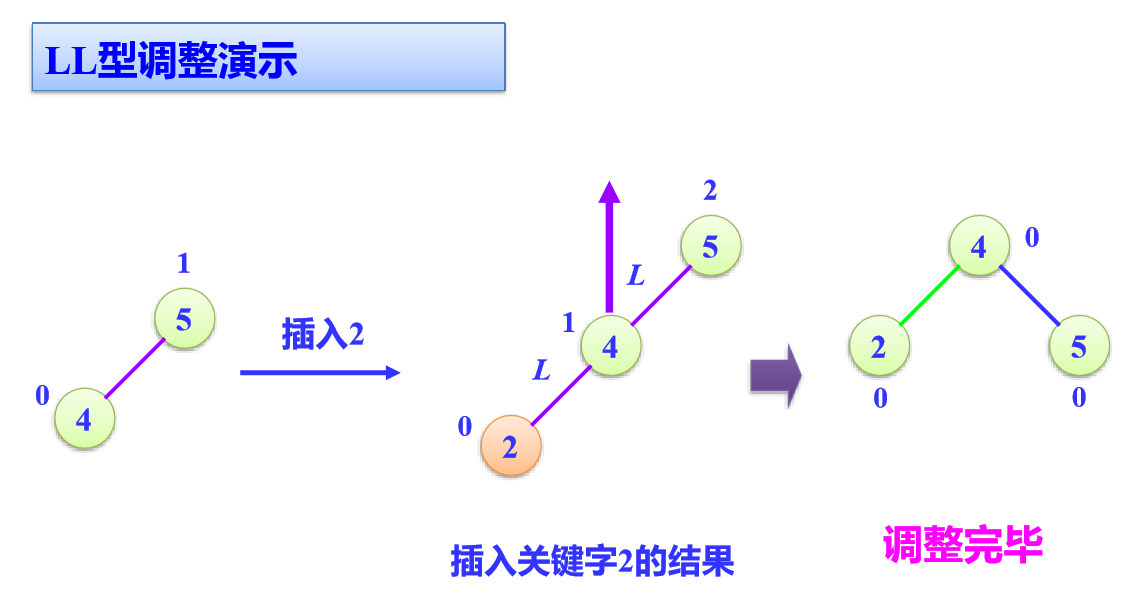
1.LL旋转(右单旋转)
2.RR旋转(左单旋转)

3.LR平衡旋转(先左后右双旋转)
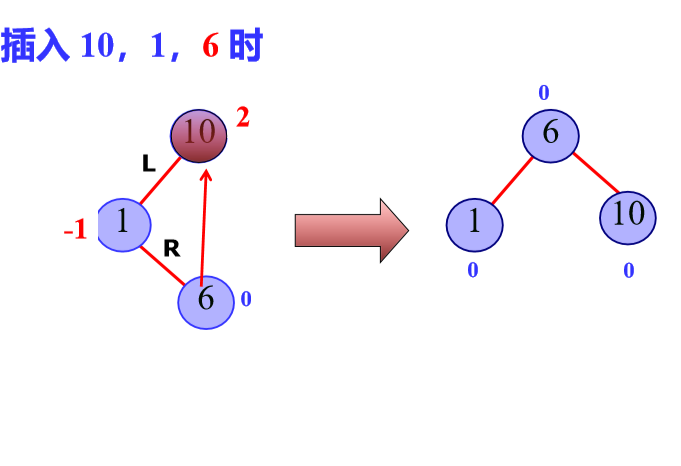
4.RL平衡旋转(先右后左双旋转)
五、哈希表
哈希函数的选择原则:
1、
若哈希函数是一个一一对应的函数,则在查找时,只需要根据哈希函数对给定关键字的某种运算得到待查找结点的存储位置,无需进行比较。
2、
一般情况下,散列表的空间要比结点的集合大,虽然浪费了一部分空间但是却提高了查找的效率,散列表空间为m,填入表中结点数为n,则比值n/m成为哈希表的装填因子,一般取0.65~0.9之间。
3、
哈希函数应当尽量简单,其值域必须在表长的范围之内,尽量不要产生“冲突”(两个关键字得到相同的哈希地址)。
重点:
如何处理哈希冲突:


六、难点:
二叉排序树的删除操作:
1.
删除操作较复杂需要分三中情况:
(1)删除节点的左孩子为空
(2)删除节点的右孩子为空
(3)删除节点有左右子树
2.
函数需要用到&符号,这需要对实参进行删除。
3.
申请空间后删除记得使用free()。
4.
代码实现:
void DeleteNode(BTree& T, int x)
{
if (T == NULL)
return;
if (x > T->data)
DeleteNode(T->rchild, x);
else if (x < T->data)
DeleteNode(T->lchild, x);
else
{
if (T->lchild == NULL) 删除节点的左孩子为空
{
BTree temp = T;
T = T->rchild;
free(temp);
}
else if (T->rchild == NULL) 删除节点的右孩子为空
{
BTree temp = T;
temp = temp->rchild;
free(temp);
}
else 删除节点有左右子树
{
BTree pre, temp;
pre = T;
temp = T->lchild;
{
pre = temp;
temp = temp->rchild;
}
T->data = temp->data;
if (pre != T)
pre->rchild = temp->lchild;
else
pre->lchild = temp->lchild;
free(temp);
}
}
}