一、数据结构
思维导图

1.算法的特点:
明确-算法应该是明确的,毫不含糊的。它的每个步骤,和它们的输入/输出的应明确和必须导致只有一个意思。
输入-算法应该具有0个或多个明确的定义输入
输出-算法应该有1个或多个明确定义的输出,并且应当匹配所需的输出。
有限性-算法必须终止在有限的之后的步骤。
可能性-应当与可用资源的可行性。
独立-算法应该有逐步的方向,应该是独立于任何编程代码。
2.基本概念
数据——所有能被计算机识别、存储和处理的符号的集合。
数据元素——是数据的基本单位,具有完整确定的实际意义。
数据对象——具有相同性质的数据元素的集合,是数据的一个子集。
数据结构——是相互之间存在一种或多种特定关系的数据元素的集合,表示为:
Data_Structure=(D, R)
数据类型——是一个值的集合和定义在该值上的一组操作的总称。
抽象数据类型——由用户定义的一个数学模型与定义在该模型上的一组操作,
它由基本的数据类型构成。
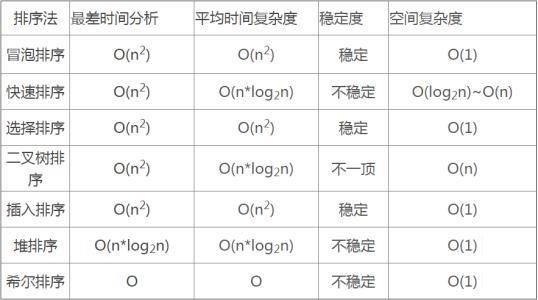
3.时间复杂度和空间复杂度
(1)时间复杂度是指执行算法所需要的计算工作量。
时间复杂度是一个函数,它定性描述了该算法的运行时间。这是一个关于代表算法输入值的字符串的长度的函数。时间复杂度常用大O符号表述,不包括这个函数的低阶项和首项系数。
(2)空间复杂度是指执行这个算法所需要的内存空间。
空间复杂度需要考虑在运行过程中为局部变量分配的存储空间的大小,它包括为参数表中形参变量分配的存储空间和为在函数体中定义的局部变量分配的存储空间两个部分。
常见的时间复杂度有:
常数阶O(1),
对数阶O(log2 n),
线性阶O(n),
线性对数阶O(n log2 n),
平方阶O(n^2),
立方阶O(n^3)
k次方阶O(n^K),
指数阶O(2^n)。
随着n的不断增大,时间复杂度不断增大,算法花费时间越多。
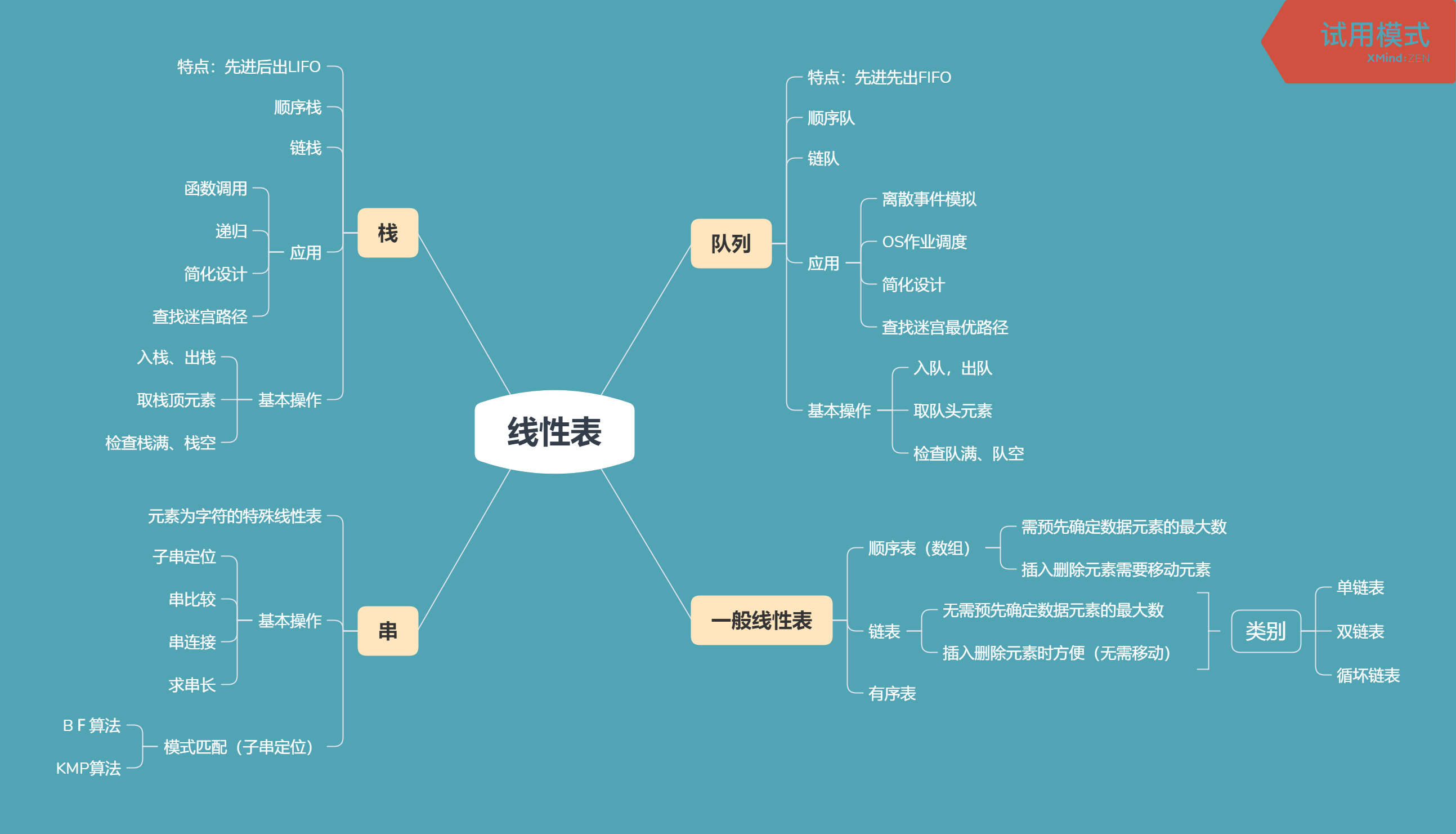
二、线性表
思维导图
顺序表:
(一)基础知识:
1.
元素-存储在数组中的每个项被称为一个元素
2.
索引-在一个数组元素所在的每个位置,是具有一个用于识别该元素的数值索引。
(二)结构体:
typedef int Elemtype;//EkemType类型实际上是int
typedef struct{
Elemtype deta[Maxsize];//存放顺序表中的元素
int length;//顺序表的长度
}SpList;
(三)基本操作:
遍历-一个一个打印所有的数组元素。
插入-给定索引处添加元素。
删除-删除给定索引处的元素。
搜索(查找)-搜索用特定索引或元素值。
修改(更新)-修改给定索引处的元素值。
1.初始化顺序表:InitList(SpList*&L)时间复杂度O(1)
2.销毁顺序表:DestroyList(Splist*L)时间复杂度O(1)
3.输出顺序表:DispList(Splist*L)时间复杂度(ListLength(L))
4.获取L中第i个元素的值,存放在e中:GetElem(SpList*L,int ####i,ElemType&e)时间复杂度:O(1)
5.按元素值查找位置:LocateElem(Splist*L,Elemtype e)时间复度O(ListLength(L))
6.插入元素:ListInsert(Splist*&L,int i, ElemType &e)时间复杂度O(ListLength(L))
7.删除元素:ListDelete( Splist*&L,int i, ElemType &e) 时间复杂度(ListLength(L)
链表
(一)结构体
typedef struct LNode//定义单链表节点
{
Elemtype data;//数据域
struct LNode*next;//指向后继节点
}LinkList;
(二)基本操作
1.
初始化:InitList(L)时间复杂度O(1)
2.
销毁:DestroyList(LinkLIst*&L)时间复杂度O(1)
3.
判断是否为空:ListEmpty(LinkList*L) 时间复杂度O(1)
4.
求链长:Listlength(LinkList*L)时间复杂度为O(n)
5.
输出线性表DispList(L)时间复杂度O(n)
6.
求指定数据的某个数据元素 GetElem(LinkList*L,int i,ElemType &e)时间复杂度O(n)
7.
插入:LinkInsert(&L,i,&e)时间复杂度O(n)
8.
删除:ListDelete(&L,i,&e)时间复杂度O(n)
头插法
s = new LNode;
s->data = a[i];
s->next = L->next;
L->next = s;
尾插法
L =new Lnode;
r = L;
s = new LNode;
s->data = a[i];
r->next = s;
r = s;
栈
1.介绍
(1)
后进先出(LIFO),插入和删除都在同一端(栈顶)进行
(2)
用于:语法检查、计算表达式的值、实现递归过程、函数调用、迷宫问题、符号匹配。
2.结构体:
顺序栈
typedef struct
{
Elemtype data[MaxSize];
int top;//栈顶位置
}SpStack;
链栈
typedef struct linknode
{
Elemtype data;
struct linknode *next;
}LiStack;
3.STL-stack用法
stack
入栈,如例:s.push(x)。
出栈,如例:s.pop();注意,出栈操作只是删除栈顶元素,并不返回该元素。
访问栈顶,如例:s.top()。
判断栈空,如例:s.empty(),当栈空时,返回true。
访问栈中的元素个数,如例:s.size()。
队列
1.队列和循环队列
(1)
先进先出(FIFO),一端(队尾)插入,另一端(队首)删除,可以以数组或链表来模拟。
(2)
用于宽度优先遍历
(3)
以n个位置的数组来存储队列时,线性队列中最多可以存储n个元素,循环队列可以存储n-1个元素。
(4)
循环队列中,如果以head表示队首,tail表示下一个插入位置。
2.结构体:
顺序队:
typedef struct
{
Elemtype data[MaxSize];
int front;
int rear
}SqQueue;
链队
typedef struct QNode
{
Elemtype data;
struct QNode *next;
}QNode;
typedef struct
{
QNode *front;
QNode *rear;
}
3.STL-queue的用法:
queue
1.
入队,如例:q1.push(x); 将x接到队列的末端。
2.
出队,如例:q1.pop(); 弹出队列的第一个元素,注意,并不会返回被弹出元素的值。
3.
访问队首元素,如例:q1.front(),即最早被压入队列的元素。
4.
访问队尾元素,如例:q1.back(),即最后被压入队列的元素。
5.
判断队列空,如例:q1.empty(),当队列空时,返回true。
6.
访问队列中的元素个数,如例:q1.size()。
串
1.定义
串:由零个或多个字符组成的有限序列。记为: s=’a1a2a3……an’ (n>=0)
串名:s
串值: a1a2a3……an
串长:n
子串:串中任意个连续的字符组成的子序列
任意串是其自身的子串
主串:包含子串的串。
位置:字符在串中的序号称为该字符在串中的位置。
空格串:由一个或多个空格组成的串,长度为空格个数。
空串:零个字符的串,用Φ表示。空串是任意串的子串
串相等:两个串长度相等且各个对应位置的字符也相等
2.空串和空白串有无区别?
答:有区别。
空串(Null String)是指长度为零的串;
而空白串(Blank String),是指包含一个或多个空白字符‘ ’(空格键)的字符串.
3.补充
“空串是任意串的子串;任意串S都是S本身的子串,除S本身外,S的其他子串称为S的真子串。”
4.string的简单用法
a) string s; //生成一个空字符串s
b) string s(str) //拷贝构造函数 生成str的复制品
c) string s(str,stridx) //将字符串str内“始于位置stridx”的部分当作字符串的初值
d) string s(str,stridx,strlen) //将字符串str内“始于stridx且长度顶多strlen”的部分作为字符串的初值
e) string s(cstr) //将C字符串作为s的初值
f) string s(chars,chars_len) //将C字符串前chars_len个字符作为字符串s的初值。
g) string s(num,c) //生成一个字符串,包含num个c字符
h) string s(beg,end) //以区间beg;end(不包含end)内的字符作为字符串s的初值
i) s.~string() //销毁所有字符,释放内存
5.难点
KMP算法
(1)求next函数值
//next函数求值
void get_next(HString &S,int *p){
int i = 0, j = 0;
i = 0; *p = 0;
while (i<S.length-1)
{
if (j==0||S.ch[i]==S.ch[j-1]){
i++; j++;
p[i] = j;
}
else
{
j = p[j-1];
}
}
}
(2)求next函数改进算法
//KMP模式匹配改进算法
void get_nextval(HString &S, int *p){
int i = 0, j = 0;
i = 0; *p = 0;
while (i < S.length - 1)
{
if (j == 0 || S.ch[i] == S.ch[j - 1]){
i++; j++;
if (S.ch[i]!=S.ch[j-1])
{
p[i] = j;
}
else{
p[i] = p[j-1];
}
}
else
{
j = p[j - 1];
}
}
}
(3)KMP实现定子串位置函数
//KMP模式匹配算法
int Index_KMP(HString T,HString S,int pos,int *p){
int i = pos, j = 0;
while (i<S.length&&j<T.length)
{
if (S.ch[i]==T.ch[j])
{
i++; j++;
}
else
{
j = p[j];
if (j==0)
{
i++;
}
else
{
j--;
}
}
}
if (j>=T.length)
{
return i - T.length+1;
}
else
{
return 0;
}
}