


因为数据很水,bfs都可以过。
然后后面数据被加强了,所以还是来看看正解吧!


#pragma GCC optimize(2) #include<bits/stdc++.h> #define N 1003 #define M 100003 #define re register using namespace std; int read() { int x=0,f=1;char s=getchar(); while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();} while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();} return x*f; } void print(int x) { if(x<0)x=-x,putchar('-'); if(x>9)print(x/10); putchar(x%10+'0'); } struct EDGE{ int nextt,to,no; }w[M]; struct edge{ int x,y; }e[M]; struct qnode{ int u,op; }; int n,m; int tot=0; int head[N],f[N][2],t[N][3],ans[N][N];//记录最长次长的距离和到达的节点 void add(int a,int b) { tot++; w[tot].nextt=head[a]; w[tot].to=b; head[a]=tot; } queue<qnode>q; void work(int S) { for(re int i=1;i<=n;++i) for(re int j=0;j<=1;++j) f[i][j]=-1,t[i][j]=0; while(!q.empty())q.pop(); for(re int i=head[S];i;i=w[i].nextt) { re int v=w[i].to; f[v][0]=1;t[v][0]=v; q.push(qnode{v,0}); } while(!q.empty()) { int x=q.front().u; int op=q.front().op;q.pop(); for(re int i=head[x];i;i=w[i].nextt) { re int v=w[i].to; if(v==S)continue; if(f[v][0]==-1) { f[v][0]=f[x][op]+1; t[v][0]=t[x][op]; q.push(qnode{v,0}); } else { if(f[v][1]!=-1||t[v][0]==t[x][op])continue; f[v][1]=f[x][op]+1; t[v][1]=t[x][op]; q.push(qnode{v,1}); } } } } int main() { freopen("railway.in","r",stdin); freopen("railway.out","w",stdout); n=read();m=read(); for(re int i=1;i<=m;++i) { e[i].x=read(); e[i].y=read(); add(e[i].x,e[i].y); } for(re int i=1;i<=n;++i) { work(i); for(re int j=1;j<=n;++j) ans[i][j]=f[j][1]; } for(int i=1;i<=m;++i) { print(ans[e[i].x][e[i].y]); putchar(' '); } putchar(' '); }


下面我们把那n个矩阵称为修改矩阵,查询的称为查询矩阵。
求两个矩阵的交我们可以把修改矩阵转为两个前缀矩阵相减。
下面画图说一下具体过程(灵魂画手上线)(这里%一下cjr大佬):
我们首先把所有的修改矩阵和查询矩阵按照x从小到大排序。
然后扫描的从左往右扫。
这幅图我们会先扫到修改矩阵的左端。
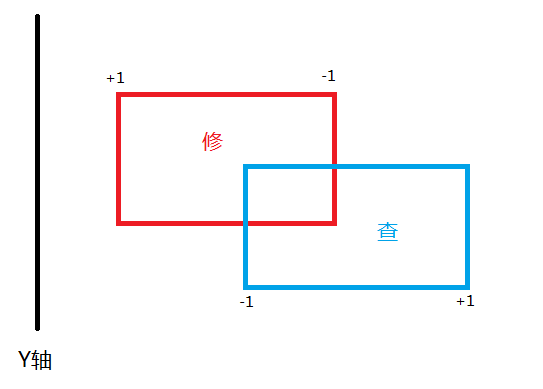
显然交就是中间那一块。
然后我们把修改矩阵分为两个前缀矩阵s1和s2

此时我们知道s1在y轴上占有下图括号括起来的宽度,面积为sum(用线段树维护即可)
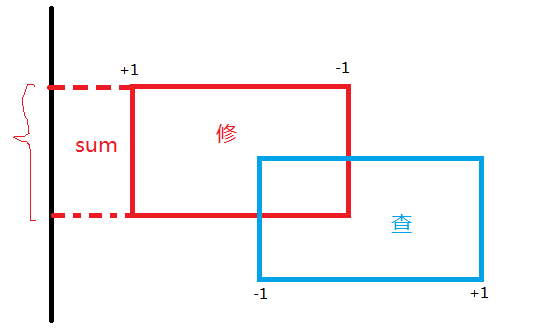
然后继续往后扫。扫到了查询矩阵的左端,我们可以对答案做出贡献。
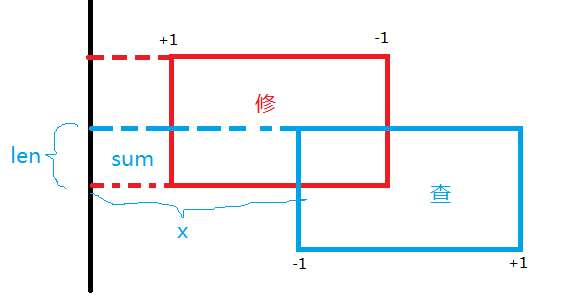
在线段树上查一下,发现len和sum如上图所示。
然后ans更新一下为len*x - sum(负的,因为此时查询矩阵端点为负)。也就是中间那一坨。可以说是查询矩阵的前缀矩阵与修改前缀矩阵的交。
然后再往后扫,扫到了修改矩阵的右端点,我们再更新线段树上的信息。
此时线段树上的len就为0了,sum是下图涂红的那一块(注意是负的)。
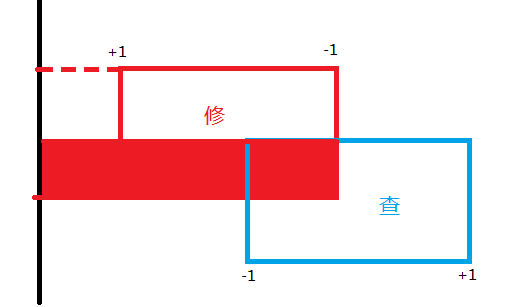
因为前面还有一个正的sum,两个sum合起来就是下图涂红的那一块(注意此时sum还是负的)。
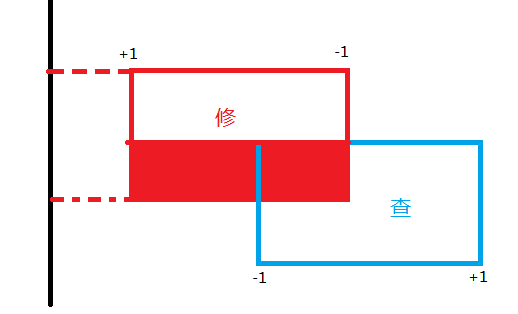
再往后扫到了查询矩阵的右端点,又可以更新答案。
len*x-sum就是下面这样(len为0,-sum因为sum本身是负的,-sum就是正的)
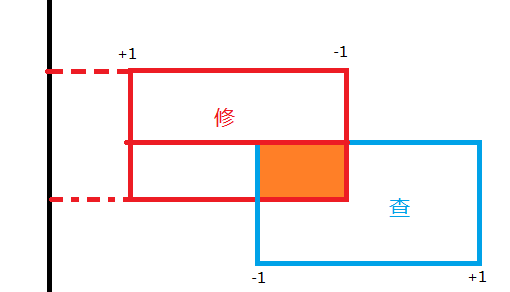
然后我们就求出交了。
很巧妙啊(反正我想不到的)。
代码就是简单的线段树了

#include<bits/stdc++.h> #define N 500003 #define LL long long #define INF 2100000000 using namespace std; int read() { int x=0,f=1;char s=getchar(); while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();} while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();} return x*f; } struct EDGE{ int l,r,h,id; int f; //f标记1,-1 bool operator<(const EDGE &a)const{return h<a.h;} }w[N*4]; struct data{LL sum;int len;};//区间和//区间长度 struct Node{//这里线段树开个结构体比较方便 int l,r;//左右儿子区间 int t2; LL t1; data res; }q[N*4]; LL ans[N]; void build(int k,int l,int r) { q[k].l=l;q[k].r=r; if(l==r) return; int mid=(l+r)>>1; build(k<<1,l,mid); build(k<<1|1,mid+1,r); } data merge(data a,data b) { return (data){a.sum+b.sum,a.len+b.len}; } void pushdown(int k,int l,int r) { int mid=(l+r)>>1; int lc=k<<1,rc=k<<1|1; q[lc].t1+=q[k].t1;q[lc].t2+=q[k].t2; q[lc].res.sum+=(mid-l+1)*q[k].t1; q[lc].res.len+=(mid-l+1)*q[k].t2; q[rc].t1+=q[k].t1;q[rc].t2+=q[k].t2; q[rc].res.sum+=(r-mid)*q[k].t1; q[rc].res.len+=(r-mid)*q[k].t2; q[k].t1=0;q[k].t2=0; } void modify(int k,int l,int r,LL val,int f) { if(q[k].l>=l&&q[k].r<=r) { q[k].t1+=val*f; q[k].t2+=f; q[k].res.sum+=val*f*(q[k].r-q[k].l+1); q[k].res.len+=f*(q[k].r-q[k].l+1); return; } int mid=(q[k].l+q[k].r)>>1; pushdown(k,q[k].l,q[k].r); if(l<=mid)modify(k<<1,l,r,val,f); if(r>mid)modify(k<<1|1,l,r,val,f); q[k].res=merge(q[k<<1].res,q[k<<1|1].res); } data query(int k,int l,int r) { data tmp={0,0}; if(q[k].l>=l&&q[k].r<=r)return q[k].res; int mid=(q[k].l+q[k].r)>>1; pushdown(k,q[k].l,q[k].r); if(l<=mid)tmp=query(k<<1,l,r); if(r>mid)tmp=merge(tmp,query(k<<1|1,l,r)); return tmp; } int n,m; int main() { // freopen("intersec.in","r",stdin); // freopen("intersec.out","w",stdout); n=read();m=read(); int W=read(),L=read(); int maxn=-INF; int tot=0; for(int i=1;i<=n;++i) { int x1=read(),y1=read(),x2=read(),y2=read(); w[++tot]=(EDGE){y1+1,y2,x1,0,1}; w[++tot]=(EDGE){y1+1,y2,x2,0,-1}; maxn=max(maxn,y2); } for(int i=1;i<=m;++i) { int x1=read(),y1=read(),x2=read(),y2=read(); w[++tot]=(EDGE){y1+1,y2,x1,i,-1}; w[++tot]=(EDGE){y1+1,y2,x2,i,1}; } sort(w+1,w+tot+1); build(1,0,maxn); for(int i=1;i<=tot;++i) { if(!w[i].id)modify(1,w[i].l,w[i].r,w[i].h,w[i].f); else { data tmp=query(1,w[i].l,w[i].r); ans[w[i].id]+=w[i].f*((LL)tmp.len*w[i].h-tmp.sum); } } for(int i=1;i<=m;++i)printf("%lld ",ans[i]); } /* 2 2 6 6 1 1 3 3 4 2 5 4 2 2 6 3 1 1 6 6 */
然后在lemon上测的时候不知道为什么第三个点RE了(第三个点???)
如果有大佬能指点一下就感激不尽了!(这就是为什么我这一篇没有设密码的原因)。


先上题解!


我这里主要是想说一下为什么方程是这个亚子的。
增加或删除一个数,指的是从还需要选的数的集合里删去。
增加很好理解,因为多了一个数j,所以i--->i+1,x--->x+j。
删除是因为把j从备选集合里删去了,本来它会对选出的数有贡献的,现在删去就要把贡献减去。
背包我们可以先预处理一下,每次枚举这一位填什么数的时候,看背包数方案是否为0.
如果为0说明这一位不能为j,继续枚举,不为0这说明这一位为j是合法的,同时把j从备选集合里删去。
因为集合里是还没确定位置的数。
j从9到0枚举保证最后答案最大。

#include<bits/stdc++.h> #define N 1003 #define LL long long #define mod 998244353 using namespace std; int read() { int x=0,f=1;char s=getchar(); while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();} while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();} return x*f; } void print(int x) { if(x<0)x=-x,putchar('-'); if(x>9)print(x/10); putchar(x%10+'0'); } int len,num=0; int flagg=0; int tong[13],f[N][13]; int tot=0; int SUM=0; char s[N]; void add(int x) { for(int i=num;i>=0;--i) for(int j=0;j<11;++j) f[i+1][(j+x)%11]=(f[i+1][(j+x)%11]+f[i][j])%mod; tong[x]++;num++; } void del(int x) { for(int i=0;i<=num;++i) for(int j=0;j<11;++j) f[i+1][(j+x)%11]=(f[i+1][(j+x)%11]-f[i][j]+mod)%mod; tong[x]--;num--; } int main() { freopen("sort.in","r",stdin); freopen("sort.out","w",stdout); scanf("%s",s+1); len=strlen(s+1); f[0][0]=1; for(int i=1;i<=len;++i) { SUM=(SUM+s[i]-'0')%11; add(s[i]-'0'); } int half=SUM*6%11;//6是2的inv int s0=half,s1=half; for(int i=1;i<=len;++i) { int S,pos; if(i%2==1)pos=len/2-i/2,S=s0; else pos=(len+1)/2-(i+1)/2,S=s1;//当前是奇数说明要找下一位偶数的背包 int j; for(j=9;j>=0;--j) { if(!tong[j])continue; del(j); if(f[pos][S])break; add(j); } if(i%2==1)s1=(s1-j+11)%11; else s0=(s0-j+11)%11; putchar(j+'0'); } }
