[九省联考2018]一双木棋chess

传送门

这道题乍一看思路只有打个暴力。

题目要求：一个格子可以落子当且仅当这个格子内没有棋子且这个格子的左侧及上方的所有格子内都有棋子，即棋子一定都分布在左上角。

也就是说涂了色的格子的形状一定是下面这样的，我们考虑横边为1，竖边为0，这个格子的所有边就是101010（没包括其他边界，只看蓝色部分），考虑轮廓线做法

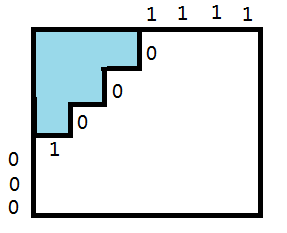初始状态为0000001111111，结束状态为1111111000000

而关于双方都选择最优策略，我们可以这样考虑，以A为标准，A想使得差值尽量大，B想使得差值尽量小，这是等价的。每次判断是先手后手，分别取max和min就好

然后我们考虑如何状态转移，我们可以发现，走一步不过是01->10（可自己画图看一下），于是我们用3异或巧妙地进行处理。

我们是用dfs进行状态的转移的，而且是先递归到最后一层，再一层一层把贡献累加回最初的状态（这是比较重要的思想）

至于每一次位置的确定，是先y=m，x=1，从右上（其实就是轮廓线的末端）往回推（可以自己手动模拟一下，还是很巧妙的）

#include<bits/stdc++.h>
#define INF 2100000001
#define N 12
using namespace std;
int read()
{
    int x=0,f=1;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    return x*f;
}
int a[N][N],b[N][N],dp[4200000],used[4200000],n,m;
int dfs(int sta,int who)//先手1，后手0 
{
    if(used[sta]) return dp[sta];
    used[sta]=1;
    if(who) dp[sta]=-INF; 
    else dp[sta]=INF;
    int x=1,y=m;
    for(int i=0;i<n+m-1;++i)//01->10
    {
        if((sta>>i)&1&&!(sta>>(i+1)&1))//位运算要小心（&1要括进去） 
        {
            int tmp=sta^(3<<i);
            if(who) dp[sta]=max(dp[sta],dfs(tmp,who^1)+a[x][y]);//先手把差距拉大 
            else dp[sta]=min(dp[sta],dfs(tmp,who^1)-b[x][y]);//后手把差距减小 
        }
        if((sta>>i)&1) y--;//相当于是沿着轮廓线回走，退到线内，为下一重循环准备 
        else x++;
    }
    return dp[sta];
}
int main()
{
    n=read(),m=read();
    for(int i=1;i<=n;++i)
      for(int j=1;j<=m;++j) 
        a[i][j]=read();
    for(int i=1;i<=n;++i)
      for(int j=1;j<=m;++j) 
        b[i][j]=read();
    //横为1，竖为0
    used[(1<<(n+m))-(1<<n)]=1;//最终状态 11110000
    printf("%d
",dfs((1<<m)-1,1));
}