BP神经网络
起源:线性神经网络与单层感知器
古老的线性神经网络,使用的是单层Rosenblatt感知器。该感知器模型已经不再使用,但是你可以看到它的改良版:Logistic回归。
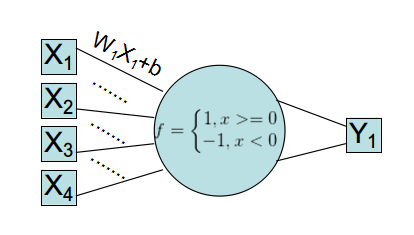
可以看到这个网络,输入->加权->映射->计算分类误差->迭代修改W、b,其实和数学上的回归拟合别无二致。
Logistic回归对该模型进行了改良:
线性神经网络(回归)使用的LMS(最小均方)的数学原理其实可由最大似然估计+假设误差概率模型得到。(详见Andrew Ng视频)
在二类分类(误差非0即1)情况下,适用于连续型数据的最小均方显然不是很好的cost函数,会引起梯度过大。
仿照线性回归假设误差服从正态分布建立概率模型,Logistic回归假设误差服从二项分布建立概率模型。
Logistic函数的(0~1连续特性)在这里充当着,由输入评估概率的角色,而不是像下面的BP网络一样,起的是高维空间非线性识别作用。
该手法同样在RBM限制玻尔兹曼机中使用。
实际上,这两种模型的起源都是最小二乘法的线性回归。不同的是,早期的解决线性回归使用的矩阵解方程组,求得参数。
而基于梯度下降使目标函数收敛的数学方法,在计算神经科学领域,就变成神经网络了。
Part I :BP网络的结构与工作方式
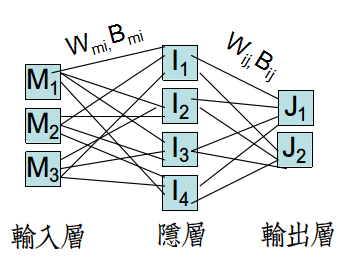
BP网络中使用隐层(HideLayer)设定,目的是通过全连接的网络+非线性Sigmoid函数,疯狂地通过特征空间映射来区分非线性数据。
注意,BP网络的非线性处理能力主要来自于隐层结构,而不单单是非线性激活函数。
所以BP网络的这种结构称为多层感知器(MLP,Multi-layer Perceptron)
从数学上是很难解释原理的。(与之相对的是SVM支持向量机,最大化间隔数学原理让你竟无言以对)。
隐层层数和每层的神经元个数决定着网络复杂度,已有数据表明(单、双隐层), 每层神经元个数与样本个数相近,网络效率最高。
输出层很特殊,如果需要多类分类的话,需要自己设计输出方式。常用的是通过0/1二进制编码来设计。
如00、01、10、11表示不同的类,这样的方式需要log2(K)+1的神经元,尽可能减轻整个网络的压力,毕竟神经网络用的是全连接。
BP网络的工作方式分为两部分:
①FP(Front Propagation)前向传播:输入->线性加权传至隐层->在隐层Sigmoid并输出->线性加权传至输入层
->输入层使用Sigmoid(或线性函数)处理输入,进行分类,计算误差并累加到总误差(目标函数)
②BP(Back Propagation) 反向传播:从输入层开始,由当前处理单条数据的误差,通过梯度法更新Wij、Bij。
由于网络的特殊性,此时Wmi、Bmi的更新依赖于Wij、Bij,只能反向更新。
BP网络训练数据有两种方法:
①单样本串行<类似随机梯度算法>:按顺序/随机输入每个样本,每次迭代只对一个样本执行FP、BP。直至单个样本误差收敛,退出迭代。
②批样本并行<类似批梯度算法>:按顺序输入每个样本,每次迭代对每个按顺序执行FP、BP,累计总误差。
执行完毕之后,算一次迭代,继续从第一个样本开始,进行第二次迭代。直至总误差收敛,退出迭代。
由于串行每次迭代只用了一个样本,因而总迭代次数应该是并行的M倍,否则误差很大。
批样本并行计算可以直观看到总误差,一般用来调参数,确认收敛情况。
而单样本串行计算,则更多的是在调完参数后,观察是否提升正确率。
Part II:BP过程的公式推导
定义ui,vi,uj,vj,分别是隐层、输入层的I/O。
Logistic-Sigmoid函数的导数:S′(x)=S(x)(1−S(x))
输出层误差:ej=dj−vjJ,其中d是真值,v是预测值,由于输出层自行设计,所以分类->真值之间需要加工处理。
输出层总误差(LMS目标函数):e=12∑Jj=1e2j
输出层第j个神经元的输出:vjJ=S(ujJ)
输出层第j个神经元的输入:ujJ=∑Ii=1(Wij⋅viI+bij)
Wij的梯度:∂e∂Wij=∂e∂ej⋅∂ej∂vjJ⋅∂vjJ∂ujJ⋅∂uiI∂Wij==−ej⋅S′(ujJ)⋅viI
求导使用的是链式法则(最好复习一遍高数),它的链式:e−>ej−>vjJ−>ujJ−>Wij
其中∂e∂ej=ej,∂ej∂vjJ=−1,∂vjJ∂ujJ=S′(ujJ),∂uiI∂Wij=viI
定义局部梯度:δjJ=−∂e∂ej⋅∂ej∂vjJ⋅∂vjJ∂ujJ=ej⋅S′(ujJ) (δjJ将在Wmi更新中使用)。
于是:Wnewij=Woldij+α⋅δjJ⋅viI bnewij=boldij+α⋅δjJ
按照同样的方式,有Wnewmi=Woldmi+α⋅δiI⋅Mm
δiI=−∂e∂uiI的推导比较有趣,其链式:(e−>ej−>vjJ−>ujJ−>viI)−>uiI
注意由于是全连接,所以单I神经元,与后一层全部J神经元有关,借用δj的导数式,括号部分=∑Jj=1Wij⋅δj
结合上面的推导,有:δiI=∑Jj=1Wij⋅δj⋅∂viI∂uiI=∑Jj=1Wij⋅δj⋅S′(uiI)
这样,即可通过先计算δI 、δJ这两个局部梯度的向量,然后拼成W的完整梯度,进而使用梯度法。
Part III:参数调整与动量BP优化
BP网络非常吃参数,调整很复杂。因而推荐取100个样本,先进行小规模调参。
由于Sigmoid函数的有效定义域大概是[-3,3],因而,首先对数据进行缩放,控制在[-1,1]内最佳。
梯度法的参数调整一直是个麻烦。步长α需要根据输入数据的特征大小调整,如果特征数值过大或过小,都会导致Sigmoid函数爆掉而导致无法迭代收敛。
在梯度方面,可以使用动量BP方法。动量BP法引入动量因子λ (0<λ<1),通常取值0.1~0.8
原更新量变成:ΔWij=α⋅δjJ⋅viI=>(1−λ)(α⋅δjJ⋅viI)+λΔWoldij
动量因子的使用,适当的考虑了前次更新:
①若前后两次梯度方向相同,由于梯度值随着目标函数的减小而减小,因而上一次的较大的梯度值会加大本次梯度混合值。
②若前后两次梯度方向相反,表明可能在两个位置有极值,上一次的梯度值可以抵消本次的部分梯度值,减小更新量。
动量因子的选取要看情况,通常先取0,然后,逐步增加。过大的动量因子,会导致抵消过大,无法收敛。
关于W参数初始值:已有论文表示,应当初始化随机这个范围的值[−4∗6√LayerInput+LayerOut√,4∗6√LayerInput+LayerOut√]
这个和α一样,得根据数据情况,自行调节,过大或过小都会导致初始迭代失败。
注意:BP网络的W、b初始化非常重要,如果像Logistic回归那样直接设0, 最终迭代出来的网络就和屎一样。(比如下面的异或问题)
Part IV:测试与代码
#include "cstdio"
#include "fstream"
#include "iostream"
#include "sstream"
#include "vector"
#include "math.h"
#include "stdlib.h"
using namespace std;
#define Dim dataSet[0].feature.size()
#define M dataSet.size()
#define alpha 0.6
#define delta 0.0000001
#define gamma 0.8
struct Data
{
vector<double> feature;
int y;
Data(vector<double> feature,int y):feature(feature),y(y) {}
};
int HideLayerNum,OutputLayerNum,now_data=0;
vector<Data> dataSet,testSet;
vector<double> u_i,v_i,u_j,v_j;
vector<double> delta_j,delta_i,pdelta_j,pdelta_i;
vector< vector<double> > W_m_i,W_i_j,B_m_i,B_i_j,pW_i_j,pW_m_i;
double random(int f_in,int f_out)
{
double ret1=rand()%((int)(sqrt(6)/sqrt(f_in+f_out)*100));
double ret2=rand()%((int)(sqrt(6)/sqrt(f_in+f_out)*100));
ret1/=100,ret2/=100;
return ret1-ret2;
}
void read()
{
ifstream fin("in.txt");
string line;
double fea;int cls;
while(getline(fin,line))
{
stringstream sin(line);
vector<double> feature;
while(sin>>fea) feature.push_back(fea);
cls=feature.back();feature.pop_back();
dataSet.push_back(Data(feature,cls));
}
HideLayerNum=M-1; //隐层神经元个数=样本数-1
OutputLayerNum=1; //二类分类,一个输出即可
for(int i=0;i<Dim;i++) //初始化权W与偏置B
{
W_m_i.push_back(vector<double>(HideLayerNum,random(Dim,HideLayerNum)));
pW_m_i.push_back(vector<double>(HideLayerNum,random(Dim,HideLayerNum)));
B_m_i.push_back(vector<double>(HideLayerNum,random(Dim,HideLayerNum)));
}
for(int i=0;i<HideLayerNum;i++)
{
W_i_j.push_back(vector<double>(OutputLayerNum,random(HideLayerNum,OutputLayerNum)));
pW_i_j.push_back(vector<double>(OutputLayerNum,random(HideLayerNum,OutputLayerNum)));
B_i_j.push_back(vector<double>(OutputLayerNum,random(HideLayerNum,OutputLayerNum)));
}
}
double sigmoid(double x) {return exp(x)/(1+exp(x));}
void buildInputLayer() //build inputLayer->hideLayer
{
u_i.clear(); //re-calc
v_i.clear();
for(int i=0;i<HideLayerNum;i++)
{
double ret=0.0;
for(int m=0;m<Dim;m++) ret+=(W_m_i[m][i]*dataSet[now_data].feature[m]+B_m_i[m][i]);
u_i.push_back(ret);
v_i.push_back(sigmoid(ret));
}
}
double buildHideLayer() //build hideLayer->OutputLayer
{
double error=0.0;
u_j.clear();
v_j.clear();
for(int j=0;j<OutputLayerNum;j++)
{
double ret=0.0;
for(int i=0;i<HideLayerNum;i++) ret+=(W_i_j[i][j]*v_i[i]+B_i_j[i][j]);
u_j.push_back(ret);
v_j.push_back(sigmoid(ret));
error+=(dataSet[now_data].y-sigmoid(ret))*(dataSet[now_data].y-sigmoid(ret));
}
return error;
}
double FP()
{
buildInputLayer();
return buildHideLayer();
}
void BP()
{
delta_i.clear();
delta_j.clear();
for(int j=0;j<OutputLayerNum;j++) //calc delta_j=error*sigmoid'(u_j)=error*v_j(1-v_j)
{
double error=0.0;
error+=(dataSet[now_data].y-v_j[j]); //all error;
delta_j.push_back(v_j[j]*(1-v_j[j])*error);
}
for(int i=0;i<HideLayerNum;i++) //calc delta_i=Σ(delta_j*W_i_j)*sigmoid'(u_i)=Σ(delta_j*W_i_j)*v_i(1-v_i)
{
double ret=0.0;
for(int j=0;j<OutputLayerNum;j++) ret+=W_i_j[i][j]*delta_j[j];
delta_i.push_back(v_i[i]*(1-v_i[i])*ret);
}
for(int i=0; i<HideLayerNum; i++) //update W_i_j
for(int j=0; j<OutputLayerNum; j++)
{
double Delta=alpha*delta_j[j]*v_i[i];
W_i_j[i][j]+=(Delta*(1-gamma)+gamma*pW_i_j[i][j]);
pW_i_j[i][j]=(Delta*(1-gamma)+gamma*pW_i_j[i][j]);
B_i_j[i][j]+=alpha*delta_j[j];
}
for(int m=0; m<Dim; m++) //update W_m_i
for(int i=0; i<HideLayerNum; i++)
{
double Delta=alpha*delta_i[i]*dataSet[now_data].feature[m];
W_m_i[m][i]+=(Delta*(1-gamma)+gamma*pW_m_i[m][i]);
pW_m_i[m][i]=(Delta*(1-gamma)+gamma*pW_m_i[m][i]);
B_m_i[m][i]+=alpha*delta_i[i];
}
}
void classify()
{
/*
ifstream fin("testdata.txt");
dataSet.clear();
double fea;int cls;
string line;
while(getline(fin,line))
{
stringstream sin(line);
vector<double> feature;
while(sin>>fea) feature.push_back(fea);
cls=feature.back();feature.pop_back();
dataSet.push_back(Data(feature,cls));
}*/
now_data=0;
for(int s=0;s<dataSet.size();s++)
{
buildInputLayer();
double ret=0.0;
for(int j=0;j<OutputLayerNum;j++)
for(int i=0;i<HideLayerNum;i++)
ret+=(W_i_j[i][j]*v_i[i]+B_i_j[i][j]);
printf("test%d: origin:%d test:%lf
",now_data++,dataSet[s].y,sigmoid(ret));
}
}
double iterProcess()
{
double err=0.0;
//random
/*
now_data=rand()%M;
err=FP();
BP();*/
//batch
now_data=0;
for(int i=0;i<M;i++)
{
err+=FP();
BP();
now_data++;
}
return err;
}
int main()
{
double oldLw,newLw;
int iter=0;
read();
oldLw=iterProcess();
newLw=iterProcess();
while(fabs(oldLw-newLw)>delta)
{
oldLw=newLw;
newLw=iterProcess();
iter++;
if(iter%1000==0) printf("iter:%d %lf
",iter,newLw);
}
cout<<iter<<endl<<endl;
classify();
}
#include "cstdio"
#include "fstream"
#include "iostream"
#include "sstream"
#include "vector"
#include "math.h"
#include "stdlib.h"
using namespace std;
#define Dim dataSet[0].feature.size()
#define M dataSet.size()
#define alpha 0.6
#define delta 0.0000001
#define gamma 0.8
struct Data
{
vector<double> feature;
int y;
Data(vector<double> feature,int y):feature(feature),y(y) {}
};
int HideLayerNum,OutputLayerNum,now_data=0;
vector<Data> dataSet,testSet;
vector<double> u_i,v_i,u_j,v_j;
vector<double> delta_j,delta_i,pdelta_j,pdelta_i;
vector< vector<double> > W_m_i,W_i_j,B_m_i,B_i_j,pW_i_j,pW_m_i;
double random(int f_in,int f_out)
{
double ret1=rand()%((int)(sqrt(6)/sqrt(f_in+f_out)*100));
double ret2=rand()%((int)(sqrt(6)/sqrt(f_in+f_out)*100));
ret1/=100,ret2/=100;
return ret1-ret2;
}
void read()
{
ifstream fin("in.txt");
string line;
double fea;int cls;
while(getline(fin,line))
{
stringstream sin(line);
vector<double> feature;
while(sin>>fea) feature.push_back(fea);
cls=feature.back();feature.pop_back();
dataSet.push_back(Data(feature,cls));
}
HideLayerNum=M-1; //隐层神经元个数=样本数-1
OutputLayerNum=1; //二类分类,一个输出即可
for(int i=0;i<Dim;i++) //初始化权W与偏置B
{
W_m_i.push_back(vector<double>(HideLayerNum,random(Dim,HideLayerNum)));
pW_m_i.push_back(vector<double>(HideLayerNum,random(Dim,HideLayerNum)));
B_m_i.push_back(vector<double>(HideLayerNum,random(Dim,HideLayerNum)));
}
for(int i=0;i<HideLayerNum;i++)
{
W_i_j.push_back(vector<double>(OutputLayerNum,random(HideLayerNum,OutputLayerNum)));
pW_i_j.push_back(vector<double>(OutputLayerNum,random(HideLayerNum,OutputLayerNum)));
B_i_j.push_back(vector<double>(OutputLayerNum,random(HideLayerNum,OutputLayerNum)));
}
}
double sigmoid(double x) {return exp(x)/(1+exp(x));}
void buildInputLayer() //build inputLayer->hideLayer
{
u_i.clear(); //re-calc
v_i.clear();
for(int i=0;i<HideLayerNum;i++)
{
double ret=0.0;
for(int m=0;m<Dim;m++) ret+=(W_m_i[m][i]*dataSet[now_data].feature[m]+B_m_i[m][i]);
u_i.push_back(ret);
v_i.push_back(sigmoid(ret));
}
}
double buildHideLayer() //build hideLayer->OutputLayer
{
double error=0.0;
u_j.clear();
v_j.clear();
for(int j=0;j<OutputLayerNum;j++)
{
double ret=0.0;
for(int i=0;i<HideLayerNum;i++) ret+=(W_i_j[i][j]*v_i[i]+B_i_j[i][j]);
u_j.push_back(ret);
v_j.push_back(sigmoid(ret));
error+=(dataSet[now_data].y-sigmoid(ret))*(dataSet[now_data].y-sigmoid(ret));
}
return error;
}
double FP()
{
buildInputLayer();
return buildHideLayer();
}
void BP()
{
delta_i.clear();
delta_j.clear();
for(int j=0;j<OutputLayerNum;j++) //calc delta_j=error*sigmoid'(u_j)=error*v_j(1-v_j)
{
double error=0.0;
error+=(dataSet[now_data].y-v_j[j]); //all error;
delta_j.push_back(v_j[j]*(1-v_j[j])*error);
}
for(int i=0;i<HideLayerNum;i++) //calc delta_i=Σ(delta_j*W_i_j)*sigmoid'(u_i)=Σ(delta_j*W_i_j)*v_i(1-v_i)
{
double ret=0.0;
for(int j=0;j<OutputLayerNum;j++) ret+=W_i_j[i][j]*delta_j[j];
delta_i.push_back(v_i[i]*(1-v_i[i])*ret);
}
for(int i=0; i<HideLayerNum; i++) //update W_i_j
for(int j=0; j<OutputLayerNum; j++)
{
double Delta=alpha*delta_j[j]*v_i[i];
W_i_j[i][j]+=(Delta*(1-gamma)+gamma*pW_i_j[i][j]);
pW_i_j[i][j]=(Delta*(1-gamma)+gamma*pW_i_j[i][j]);
B_i_j[i][j]+=alpha*delta_j[j];
}
for(int m=0; m<Dim; m++) //update W_m_i
for(int i=0; i<HideLayerNum; i++)
{
double Delta=alpha*delta_i[i]*dataSet[now_data].feature[m];
W_m_i[m][i]+=(Delta*(1-gamma)+gamma*pW_m_i[m][i]);
pW_m_i[m][i]=(Delta*(1-gamma)+gamma*pW_m_i[m][i]);
B_m_i[m][i]+=alpha*delta_i[i];
}
}
void classify()
{
/*
ifstream fin("testdata.txt");
dataSet.clear();
double fea;int cls;
string line;
while(getline(fin,line))
{
stringstream sin(line);
vector<double> feature;
while(sin>>fea) feature.push_back(fea);
cls=feature.back();feature.pop_back();
dataSet.push_back(Data(feature,cls));
}*/
now_data=0;
for(int s=0;s<dataSet.size();s++)
{
buildInputLayer();
double ret=0.0;
for(int j=0;j<OutputLayerNum;j++)
for(int i=0;i<HideLayerNum;i++)
ret+=(W_i_j[i][j]*v_i[i]+B_i_j[i][j]);
printf("test%d: origin:%d test:%lf
",now_data++,dataSet[s].y,sigmoid(ret));
}
}
double iterProcess()
{
double err=0.0;
//random
/*
now_data=rand()%M;
err=FP();
BP();*/
//batch
now_data=0;
for(int i=0;i<M;i++)
{
err+=FP();
BP();
now_data++;
}
return err;
}
int main()
{
double oldLw,newLw;
int iter=0;
read();
oldLw=iterProcess();
newLw=iterProcess();
while(fabs(oldLw-newLw)>delta)
{
oldLw=newLw;
newLw=iterProcess();
iter++;
if(iter%1000==0) printf("iter:%d %lf
",iter,newLw);
}
cout<<iter<<endl<<endl;
classify();
}
自己测试,推荐使用著名的异或问题数据集,该数据只有四个点[0,0]、[1,0]、[0,1]、[1,1] ,分类[0,1,1,0]
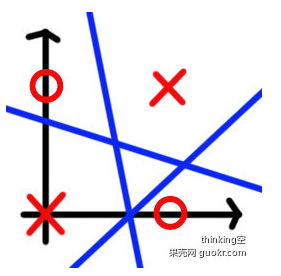
线性分类器准确无法分类,原因参见:http://www.guokr.com/blog/793310/
使用α=0.6、λ=0.8(动量因子)
如果你的BP网络代码没错的话,并行9000次, 单次迭代所有的样本SSE(误差平方和)大概是这样。
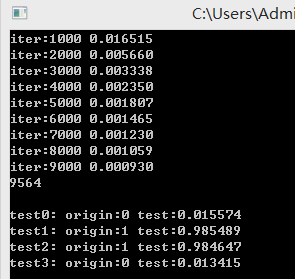
很好地解决了,这个线性不可分问题。
