Area
Time Limit: 5000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 225 Accepted Submission(s): 77
Problem Description
电子科大清水河校区是电子科大大力兴建的未来主校区,于07年秋正式迎接学生入住,目前有07、08级本科生及部分研究生在此校区学习、生活。
清水河校区位于成都高新西区的中部地带,占地约3128亩。从空中看,新校区的整体像一个长方形,南北长,东西窄。一条水渠从西北角的顶点注入,笔直的延伸到南面围墙的大概三分之一分点的地方,由此流出学校。位于这条水渠和西墙之间的是研究院,最南面的是学术交流中心和接待中心。
在本题中,假设清水河校区是一个凸多边形,水渠是一条直线,要求给出清水河校区被水渠分割成的两部分的面积。

清水河校区位于成都高新西区的中部地带,占地约3128亩。从空中看,新校区的整体像一个长方形,南北长,东西窄。一条水渠从西北角的顶点注入,笔直的延伸到南面围墙的大概三分之一分点的地方,由此流出学校。位于这条水渠和西墙之间的是研究院,最南面的是学术交流中心和接待中心。
在本题中,假设清水河校区是一个凸多边形,水渠是一条直线,要求给出清水河校区被水渠分割成的两部分的面积。

Input
输入包含多组数据。每组数据第一行是一个整数N(3<=N<=20),表示清水河校区的边数,N=0表示输入结束。随后有N行,每行有两个整数X,Y(0<=X,Y<=10000),按顺时针顺序给出清水河校区的每个顶点的坐标。最后一行包含四个整数X0,Y0,X1,Y1,(0<= X0,Y0,X1,Y1<=10000),表示水渠上的两个点的(X0,Y0),(X1,Y1)的坐标,保证这两个点一定不会重合,同时保证水渠一定穿过清水河校区。
Output
对每组数据,输出一行,按大小顺序输出清水河校区被水渠分割成的两部分的面积。面积大者在前面输出。(输出部分要四舍五入到整数)!
Sample Input
4
0 0
0 100
100 100
100 0
10 0 15 5
0
Sample Output
5950 4050
提示:
对于一个顺时针给出的多边形,如果它的顶点坐标依次是(xi,yi),0<=i<n,则它的面积为:
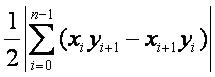
其中xn=x0,yn=y0
Source
Recommend
计算几何,求线段与直线交点 + 求多边形面积。
题意是给你一个点按顺序排列的多边形,一条直线穿过多边形,求直线分割的两部分多边形面积。面积大的先输出。
思路:因为题目给出的多边形的点是按顺时针顺序输出的,所以你可以根据叉积找出水渠代表的直线同一侧的所有顺时针的点,选一侧的所有点作为切割后的一边多边形的点集,再将直线与多边形的两个交点加到选定多边形点集合适的位置(难点)。这样分割后其中一边的多边形就确定了(点集中的点必须是顺序的),求出它的面积,再根据 多边形总面积 - 刚才求的这个多边形的面积 就是另一边多边形的面积。比较一下输出这两个面积即可。
注意:产生分割后一个多边形点集的方法。
代码:
1 #include <iostream>
2 #include <cmath>
3 using namespace std;
4 #define eps 1e-10
5 /********** 定义点 **********/
6 struct Point{
7 double x,y;
8 Point(double x=0,double y=0):x(x),y(y) {}
9 };
10 /********** 定义向量 **********/
11 typedef Point Vector;
12 /********** 向量 + 向量 = 向量 **********/
13 Vector operator + (Vector a,Vector b)
14 {
15 return Vector(a.x+b.x,a.y+b.y);
16 }
17 /********** 点 - 点 = 向量 **********/
18 Vector operator - (Point a,Point b)
19 {
20 return Vector(a.x-b.x,a.y-b.y);
21 }
22 /********** 向量 * 数 = 向量 **********/
23 Vector operator * (Vector a,double b)
24 {
25 return Vector(a.x*b,a.y*b);
26 }
27 /********** 2向量求叉积 **********/
28 double Cross(Vector a,Vector b)
29 {
30 return a.x*b.y-b.x*a.y;
31 }
32 int dcmp(double x) //减少精度问题
33 {
34 if(fabs(x)<eps)
35 return 0;
36 else
37 return x<0?-1:1;
38 }
39 /********** 直线交点 **********/
40 Point GetLineIntersection(Point P,Vector v,Point Q,Vector w)
41 {
42 Vector u = P-Q;
43 double t = Cross(w,u) / Cross(v,w);
44 return P+v*t;
45 }
46 /********* 求多边形面积 **********/
47 double ConvexPolygonArea(Point* p,int n)
48 {
49 double area = 0;
50 for(int i=2;i<=n-1;i++)
51 area += Cross(p[i]-p[1],p[i+1]-p[1]);
52 return area/2;
53 }
54 int main()
55 {
56 int n;
57 while(cin>>n){
58 if(n==0) break;
59 int i;
60 Point p[25];
61 for(i=1;i<=n;i++)
62 cin>>p[i].x>>p[i].y;
63 Point p0,p1;
64 cin>>p0.x>>p0.y>>p1.x>>p1.y;
65 Vector v = p1-p0;
66 Point pl[25]; //切割后的多边形之一
67 p[n+1] = p[1];
68 int num = 0;
69 //产生切割多边形
70 for(i=1;i<=n;i++){
71 int d1 = dcmp(Cross(v,p[i]-p0));
72 int d2 = dcmp(Cross(v,p[i+1]-p0));
73 if(d1>=0)
74 pl[++num] = p[i];
75 if(d1*d2<0)
76 pl[++num] = GetLineIntersection(p0,v,p[i],p[i+1]-p[i]);
77 }
78 double a1 = fabs(ConvexPolygonArea(pl,num));
79 double sum = fabs(ConvexPolygonArea(p,n));
80 double a2 = sum-a1;
81
82 int A1 = int(fabs(a1)+0.5);
83 int A2 = int(fabs(a2)+0.5);
84 if(A1>=A2)
85 cout<<A1<<' '<<A2<<endl;
86 else
87 cout<<A2<<' '<<A1<<endl;
88 }
89 return 0;
90 }
Freecode : www.cnblogs.com/yym2013