Codeforces 822C Hacker, pack your bags!

It's well known that the best way to distract from something is to do one's favourite thing. Job is such a thing for Leha.

So the hacker began to work hard in order to get rid of boredom. It means that Leha began to hack computers all over the world. For such zeal boss gave the hacker a vacation of exactly x days. You know the majority of people prefer to go somewhere for a vacation, so Leha immediately went to the travel agency. There he found out that n vouchers left. i-th voucher is characterized by three integers l_i, r_i,cost_i — day of departure from Vičkopolis, day of arriving back in Vičkopolis and cost of the voucher correspondingly. The duration of thei-th voucher is a value r_i - l_i + 1.

At the same time Leha wants to split his own vocation into two parts. Besides he wants to spend as little money as possible. Formally Leha wants to choose exactly two vouchers i and j (i ≠ j) so that they don't intersect, sum of their durations is exactly x and their total cost is as minimal as possible. Two vouchers i and j don't intersect if only at least one of the following conditions is fulfilled: r_i < l_j or r_j < l_i.

Help Leha to choose the necessary vouchers!

Input

The first line contains two integers n and x (2 ≤ n, x ≤ 2·10⁵) — the number of vouchers in the travel agency and the duration of Leha's vacation correspondingly.

Each of the next n lines contains three integers l_i, r_i and cost_i (1 ≤ l_i ≤ r_i ≤ 2·10⁵, 1 ≤ cost_i ≤ 10⁹) — description of the voucher.

Output

Print a single integer — a minimal amount of money that Leha will spend, or print  - 1 if it's impossible to choose two disjoint vouchers with the total duration exactly x.

Examples

input

4 5
1 3 4
1 2 5
5 6 1
1 2 4

output

5

input

3 2
4 6 3
2 4 1
3 5 4

output

-1

Note

In the first sample Leha should choose first and third vouchers. Hereupon the total duration will be equal to (3 - 1 + 1) + (6 - 5 + 1) = 5and the total cost will be 4 + 1 = 5.

In the second sample the duration of each voucher is 3 therefore it's impossible to choose two vouchers with the total duration equal to 2.

---

　　题目大意 给定n个区间，每个区间有个费用，选择两个不相交(端点也不能重叠)的区间使得它们的长度总和恰好为x，并且使得它们的费用和最小。如果无解输出-1。

　　根据常用套路，按照区间的长度进行分组。然后按照端点的大小(反正按左端点还是右端点都是一样的)进行排序。再拿两个数组跑一道前缀最小值和后缀最小值。

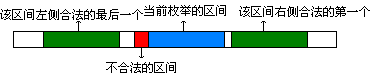
　　现在枚举每一条旅行方案，在和它的长度之和恰好为x的另一个数组中，可以用lower_bound和upper_bound快速找出两侧合法的的最后一个和第一个，然后更新一下就好了(详细可以看代码)。

Code

/**
 * Codeforces
 * Problem#822C
 * Accepted
 * Time:124ms
 * Memory:16416k
 */
#include <iostream>
#include <cstdio>
#include <ctime>
#include <cmath>
#include <cctype>
#include <cstring>
#include <cstdlib>
#include <fstream>
#include <sstream>
#include <algorithm>
#include <map>
#include <set>
#include <stack>
#include <queue>
#include <vector>
#include <stack>
#ifndef WIN32
#define Auto "%lld"
#else
#define Auto "%I64d"
#endif
using namespace std;
typedef bool boolean;
const signed int inf = (signed)((1u << 31) - 1);
const double eps = 1e-6;
const int binary_limit = 128;
#define smin(a, b) a = min(a, b)
#define smax(a, b) a = max(a, b)
#define max3(a, b, c) max(a, max(b, c))
#define min3(a, b, c) min(a, min(b, c))
template<typename T>
inline boolean readInteger(T& u){
    char x;
    int aFlag = 1;
    while(!isdigit((x = getchar())) && x != '-' && x != -1);
    if(x == -1) {
        ungetc(x, stdin);    
        return false;
    }
    if(x == '-'){
        x = getchar();
        aFlag = -1;
    }
    for(u = x - '0'; isdigit((x = getchar())); u = (u << 1) + (u << 3) + x - '0');
    ungetc(x, stdin);
    u *= aFlag;
    return true;
}

typedef class Trip {
    public:
        int l;
        int r;
        int fee;
        
        Trip(int l = 0, int r = 0, int fee = 0):l(l), r(r), fee(fee) {        }
        
        boolean operator < (Trip b) const {
            return l < b.l;
        }
}Trip;

boolean operator < (const int& b, const Trip& a) {
    return b < a.l;
}

int n, x;
vector<Trip>* a;
vector<int>* minu;        // in order
vector<int>* mind;        // in opposite order

inline void init() {
    readInteger(n);
    readInteger(x);
    a = new vector<Trip>[x];
    minu = new vector<int>[x];
    mind = new vector<int>[x];
    for(int i = 1, l, r, c; i <= n; i++) {
        readInteger(l);
        readInteger(r);
        readInteger(c);
        int len = r - l + 1;
        if(len >= x)    continue;
        a[len].push_back(Trip(l, r, c));
    }
}

int res = inf;
inline void solve() {
    for(int i = 1; i < x; i++)
        if(!a[i].empty()) {
            sort(a[i].begin(), a[i].end());
            minu[i].resize(a[i].size());
            mind[i].resize(a[i].size());
            for(int j = 0; j < (signed)a[i].size(); j++) {
                if(j == 0)    minu[i][j] = a[i][j].fee;
                else minu[i][j] = min(a[i][j].fee, minu[i][j - 1]);
            }
            for(int j = (signed)a[i].size() - 1; j >= 0; j--) {
                if(j == a[i].size() - 1)    mind[i][j] = a[i][j].fee;
                else mind[i][j] = min(a[i][j].fee, mind[i][j + 1]);
            }
        }
        
    for(int i = 1; i < x; i++) {
//        cout << i << ":" << endl;
        if(!a[i].empty()) {
            for(int j = 0; j < a[i].size(); j++) {
//                cout << a[i][j].l << " " << a[i][j].r << endl;
                Trip &t = a[i][j];
                int len = t.r - t.l + 1;
                int ulen = x - len;
                int pos = upper_bound(a[ulen].begin(), a[ulen].end(), t.r) - a[ulen].begin();
                if(pos != a[ulen].size())    smin(res, t.fee + mind[ulen][pos]);
                pos = lower_bound(a[ulen].begin(), a[ulen].end(), t.l - ulen + 1) - a[ulen].begin() - 1;
                if(pos != -1)    smin(res, t.fee + minu[ulen][pos]);
            }
        }
    }
    
    if(res == inf)
        puts("-1");
    else
        printf("%d
", res);
}

int main() {
    init();
    solve();
    return 0;
}