LeetCode: Subsets I & II

1 Subset

https://leetcode.com/problems/subsets/

Given a set of distinct integers, nums, return all possible subsets.

Note:

• Elements in a subset must be in non-descending order.
• The solution set must not contain duplicate subsets.

For example,
If nums = [1,2,3], a solution is:

[
  [3],
  [1],
  [2],
  [1,2,3],
  [1,3],
  [2,3],
  [1,2],
  []
]

思路：对于这样的题目，已经有一个直观的思路，就是DFS,使用递归。
这里面有两种递归思路，一种就是将问题拆分成子问题，如先求[1,2]的子集,根据[1,2]的子集求[1,2,3]的子集

思路一

可以用递推的思想，观察S=[], S =[1], S = [1, 2] 时解的变化。

可以发现S=[1, 2] 的解就是 把S = [1]的所有解末尾添上2，然后再并上S = [1]里面的原有解。因此可以定义vector<vector<int> > 作为返回结果res, 开始时res里什么都没有，第一步放入一个空的vecotr<int>，然后这样迭代n次，每次更新res 内容，最后返回res。

特别注意：蓝色代码一定要有，因为在接下来的循环中不断在填充results，所以在循环前要得到size

class Solution{
public:
    vector<vector<int> > subsets(vector<int> & S){
        vector<vector<int> > results;
        vector<int> result;
        if (S.empty()){
            results.push_back(result);
            return results;
        }
        results.push_back(result);
        sort(S.begin(),S.end());
        result.push_back(S[0]);
        results.push_back(result);
        for (int i = 1 ; i < S.size(); i++){
            int size = results.size();
            for (int j = 0 ; j < size; j++){
                vector<int> r(results[j].begin(),results[j].end());
                r.push_back(S[i]);
                results.push_back(r);
            }
        }
        return results;
    }
};

另一种递归思路就是使用DFS

class Solution{
public:
    vector<vector<int> > subsets(vector<int> & S){
        vector<vector<int> > results;
        vector<int> result;
        results.push_back(result);
        sort(S.begin(),S.end());
        dfs(0,result,S,results);
        return results;
    }
    void dfs(int index, vector<int> & result, vector<int> & S, vector<vector<int> > & results){
        for (int i = index; i < S.size(); i++){
            result.push_back(S[i]);
            results.push_back(result);
            dfs(i+1,result,S,results);
            result.pop_back();
        }
    }
};

2 Subsets II

https://leetcode.com/problems/subsets-ii/

Given a collection of integers that might contain duplicates, nums, return all possible subsets.

Note:

• Elements in a subset must be in non-descending order.
• The solution set must not contain duplicate subsets.

For example,
If nums = [1,2,2], a solution is:

[
  [2],
  [1],
  [1,2,2],
  [2,2],
  [1,2],
  []
]

我们以S=[1,2,2]为例:

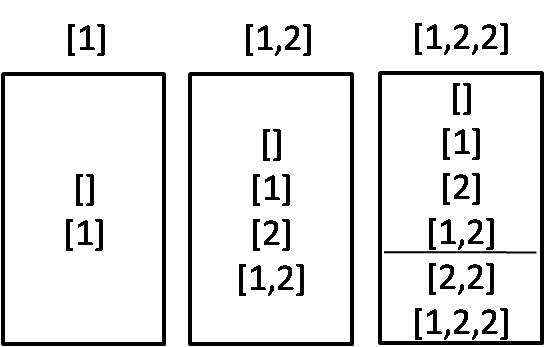
可以发现从S=[1,2]变化到S=[1,2,2]时，多出来的有两个子集[2,2]和[1,2,2]，这两个子集，其实就是 [2], [1,2]末尾都加上2 而产生。而[2], [1,2] 这两个子集实际上是 S=[1,2]的解到 S=[1]的解 新添加的部分。

因此，若S中有重复元素，可以先排序；遍历过程中如果发现当前元素S[i] 和 S[i-1] 相同，那么不同于原有思路中“将当前res中所有自己拷贝一份再在末尾添加S[i]”的做法，我们只将res中上一次添加进来的子集拷贝一份，末尾添加S[i]。

class Solution{
public:
    vector<vector<int> > subsetsWithDup(vector<int> &S){
        vector<vector<int> > results;
        vector<int> empty;
        results.push_back(empty);
        if (S.empty())
            return results;
        sort(S.begin(),S.end());
        int m = 0;
        int start = 0;
        for (int i = 0 ; i < S.size(); i++){
            if (i > 0 && S[i] == S[i-1]){
                start = m;    
            }
            else{
                start = 0;
            }
            int size = results.size();
            for (int j = start; j < size; j++){
                vector<int> r(results[j].begin(),results[j].end());
                r.push_back(S[i]);
                results.push_back(r);
            }
            m = size;
        }
        return results;
    }
};

同样有另一种解法：

class Solution {
public:
  
    
    vector<vector<int> > subsetsWithDup(vector<int> & S){
        vector<vector<int> > results;
        vector<int> result;
        results.push_back(result);
        sort(S.begin(),S.end());
        dfs(0,result,S,results);
        return results;
    }
    void dfs(int index, vector<int> & result, vector<int> & S, vector<vector<int> > & results){
        for (int i = index; i < S.size(); i++){
            if (i > index && S[i] == S[i-1])
                continue;
            result.push_back(S[i]);
            results.push_back(result);
            dfs(i+1,result,S,results);
            result.pop_back();
        }
    }
};