题目:
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
说明:
所有数字(包括目标数)都是正整数。
解集不能包含重复的组合。
示例:
输入: candidates = [10,1,2,7,6,1,5], target = 8, 所求解集为: [ [1, 7], [1, 2, 5], [2, 6], [1, 1, 6] ]
分析:主要对比一下第39题,不同之处在于:第一,数组中存在重复的元素;第二,每个数字在每个组合中只能使用一次,注意!这里是每个数字,而不是每种数字,也就是同一个位置的数字在一个组合中只能出现一次,但是不同位置的相同数值的数字可以在同一个组合中同时出现!我们以上面那个示例中的数据作为例子,对搜索结果的过程进行一次展示,如下图所示:
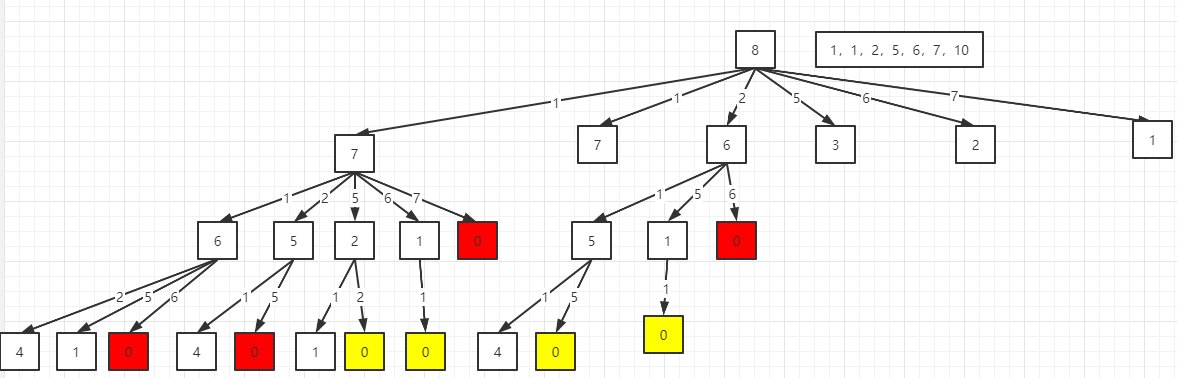
在上图中,每次向下进行一次搜索,可选取的搜索范围都是会发生变化的,因为题目要求一个数字只能在组合中出现一次,所以在一条搜索路径中,如果数组中的某个位置的数字已经使用了,那么在以后的搜索中就不能选取了,所以我们为了方便,我们要对原有的数组进行排序,然后开启下一次搜索的遍历起始元素是当前元素在数组中索引位置加1,这就能够保证不会重复使用原有的元素,同时也保证了不会产生上图中包含黄色叶子结点的路径的重复组合。
但是,还会有一种重复组合产生的可能,上面第一种重复组合的产生的原因是由于搜索路径中元素种类相同但是顺序不同所造成的,但是现在第二种重复造成的原因是因为原数组中存在相同数值的元素,所以就会一定会有相同的路径产生,这些相同的路径中元素的顺序都是一样,因为数组中有重复的元素,所以在搜索的时候,不同位置的元素就可开启一条路径,那么最终的结果就是一样的。正如上图中我没有画全的第二个子树,它和第一棵子树是一样的。那么我们需要去掉这样的重复,解决办法:
利用访问标记数组,遍历的搜索元素的时候,先判断当前这个元素是否和其在数组中前一个位置的元素相等:
如果相等就要再进一步判断,其前一个元素是否被访问过,如果访问过,那就说明这两个值相同但是位置不同的元素是在一条搜索路径中的,那就可以继续搜索;
如果不相等,那根据回溯的原理我们知道,结束一条路径的访问时,其路径上的结点对应的访问标记数组的值都会从下往上被一一置为初始值的。所以那就是重开了一条路径,而这条重开的路径最后得到的结果必然和前一个相同值开启的路径得到的结果重复。所以要跳过这个重开的路径,直接搜索其他的元素。
代码实现:
private List<List<Integer>> resList; public List<List<Integer>> combinationSum2(int[] candidates, int target) { if (candidates==null || candidates.length==0){ return new ArrayList<>(); } resList = new ArrayList<>(); List<Integer> curlist = new ArrayList<>(); Arrays.sort(candidates); boolean[] isVisited = new boolean[candidates.length]; combinationAll(candidates,target,0,curlist,isVisited); return resList; } private void combinationAll(int[] candidates, int target, int start, List<Integer> curlist,boolean[] isVisited) { if (target == 0){ resList.add(new ArrayList<>(curlist)); return; } for (int i = start; i < candidates.length; i++) { if (i > 0 && candidates[i] == candidates[i - 1] && !isVisited[i-1]){ continue; } if (candidates[i] <= target){ curlist.add(candidates[i]); isVisited[i] = true; combinationAll(candidates,target-candidates[i],i+1,curlist,isVisited); isVisited[i] = false; curlist.remove(curlist.size()-1); } } }