STL -- heap结构及算法
heap(隐式表述,implicit representation)
1. heap概述 : vector + heap算法
heap并不归属于STL容器组件,它是个幕后英雄,扮演priority queue的助手。顾名思义,priority queue允许用户以任何次序将任何元素推入容器内,但取出时一定是从优先权最高(也就是数值最高)的元素开始取。binary max heap 正是具有这样的特性,适合作为priority queue 的底层机制。
让我们做一点分析。如果使用list 作为priority queue的底层机制,元素出入操作可享常数时间。但是要找到list中的极值,却需要对整个list进行线性扫描。我们也可以改变做法,让元素插入前先经过排序,使得list的元素值总是由小到大(或由大到小),但这么一来,收之东隅却失之桑榆:虽然取得极值以及元素删除操作达到最高效率,可元素的插入却只有线性表现。
比较好的做法是以binary search tree 作为priority queue的底层机制。这么一来,元素的插入和极值的取得就有O(logN) 的表现。但杀鸡用牛刀,未免小题大做,一来binary search tree 的输入需要足够的随机性,二来binary search tree并不容易实现。priority queue 的复杂度,最好介于queue 和 binary search tree 之间,才算适得其所。bianry heap便是这种条件下的适当候选人。
所谓binary heap 就是一种complete binary tree(完全二叉树),也就是说,整棵binary tree 除了最底层的叶节点之外,是填满的,而最底层的叶节点(s)由左至右又不得有空隙。
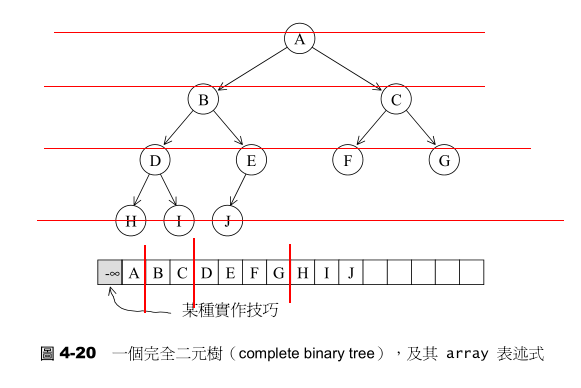
complete binary tree 整棵树内没有任何节点漏洞,这带来一个极大的好处:我们可以利用array来存储所有节点。假设动用一个小技巧,将array的#0元素保留(或设为无限大或无限小),那么当complete binary tree中的某个节点位于array的i处时,其左子节点必位于array的2i处,其右子节点比位于array的2i+1处,其父节点必位于“i/2”处。通过这么简单的位置规则,array可以轻易实现出complete binary tree。这种以array表述tree的方式,我们称为隐式表述法。
这么一来,我们需要的工具就很简单了:一个array 和 一组 heap算法(用来进行元素操作,并将某一整组数据排列成一个heap)。array的缺点是无法动态改变大小,而heap却需要这项功能,因此,以vector代替array是更好的选择。
根据元素的排列方式,heap可分为max-heap 和 min-heap两种,前者每个节点的键值(key)都大于或等于其子节点键值,后者的每个节点键值都小于或等于其子节点键值。STL提供的是max-heap。
2. heap算法
2.1 push_heap算法:上溯
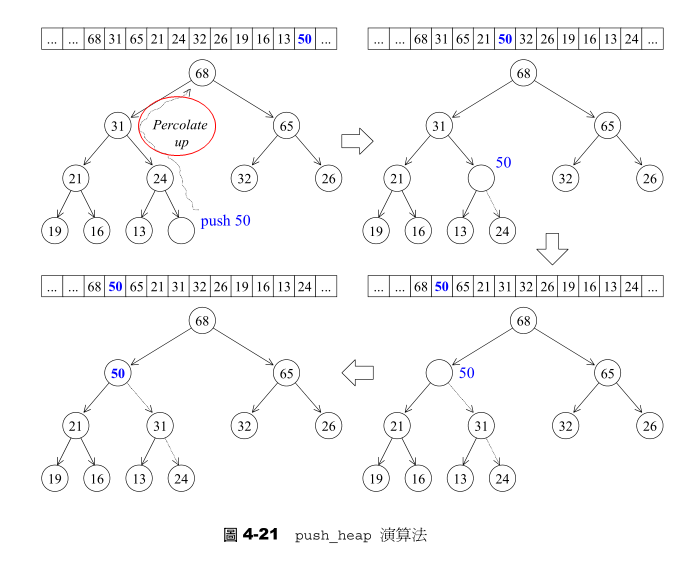
percolate_up(上溯)程序:将新节点拿来与其父节点比较,如果其键值(key)比父节点大,就父子对换位置。如此一直上溯,直到不需对换或直到根节点为止。
push_heap算法的实现细节参见相关源码。
注意:
(1)为了满足complete binary tree的条件,新加入的元素一定要放在最下一层作为叶节点,便填补在由左至右的第一个空格,也就是把新元素插入在底层vector的end()处。
(2)当push_heap函数被调用时,新元素应已置于底部容器的最尾端。
另: array无法动态改变大小,因此如果heap底层采用array,便不可以对满载的array进行push_heap操作,因为那得先在array尾端增加一个元素。如果对一个满载的array执行push_heap,该函数会将最后一个元素视为新增元素,并将其余元素视为一个完整的heap结构(实际上它们的确是),因此执行后的结果等于原先的heap。
2.2 pop_heap算法:下溯+上溯
下图是 pop_heap算法的实际操演情况。既然身为max-heap,最大值必然在根节点。pop操作取走根节点(其实是设至底部容器vector的尾端节点)后,为了满足complete binary tree的条件,必须割舍最下层最右边的叶节点,并将其值重新安插至max-heap(因此有必要重新调整heap结构)。
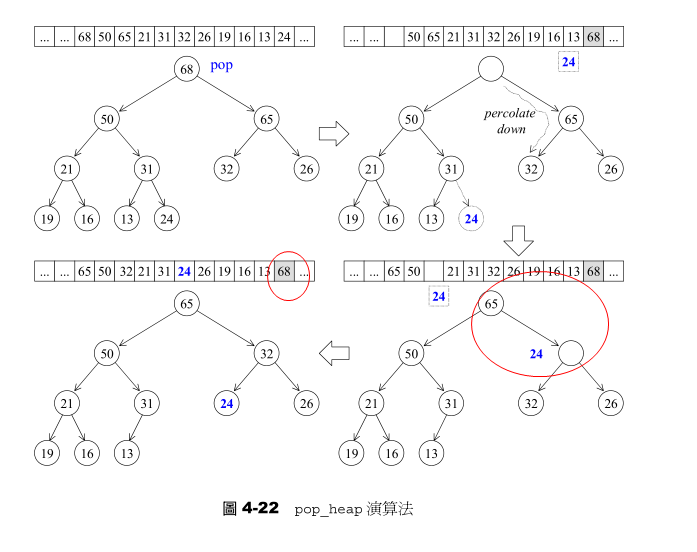
为了满足max-heap次序特性(每个节点的键值都大于或等于其子节点键值),我们执行所谓的percolate down(下溯)程序:将空间节点和其较大子节点“对调”,并持续下放,直至叶节点为止。然后将前述被割舍之元素值设给这个“已到达叶层的空间节点”,再对它执行一次percolate up(上溯)程序。
pop_heap算法的实现细节参见相关源码。
注意:
pop_heap之后,最大元素只是被置于底部容器的最尾端,尚未被取走。
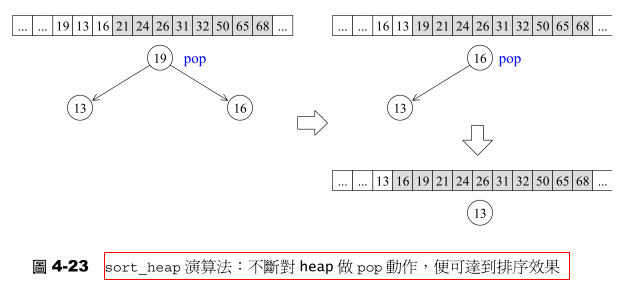
2.3 sort_heap算法
既然每次pop_heap可获得heap中键值最大的元素,如果持续对整个heap做pop_heap操作,每次将操作范围从后向前缩减一个元素(因为pop_heap会把键值最大的元素放在底部容器的最尾端),当整个程序执行完毕时,我们便有了一个递增序列。

2.4 make_heap算法
这个算法用来将一段现有的数据转化为一个heap。
make_heap算法实现参见相关源码
3. heap没有迭代器 heap的所有元素都必须遵循特别的(complete binary tree)排列规则,所以heap不提供遍历功能,也不提供迭代器。