Part 1:迪杰斯特拉( Dijkstra ) 算法
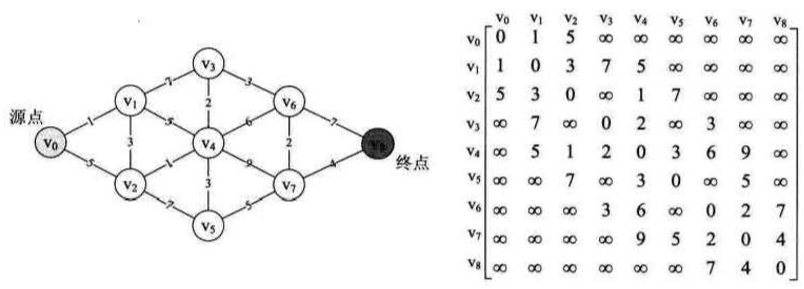
看下面这个图,要找到原点到终点的权值和最小路径,就需要这个算法的思想:
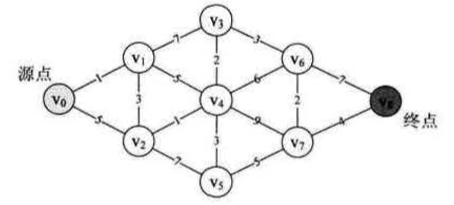
第一步先探测 v0 邻近的顶点的距离,易得 v0→v1 的权值为1,小的一批,理所当然 v1 就是继 v0 之后然后看 v1 这个点,v1 辐射到 v2 、v3 、v4 ,其权值分别为 3 、7、5 ,故 v0→v1→v2 = 4,v0 → v2 = 5,如果现在要找 v0 → v2 的距离,在刚才的分析的基础之上,易得应该走 v0 → v1 → v2,权值为 4,当然现在 v2 也已经加入了最小路径。
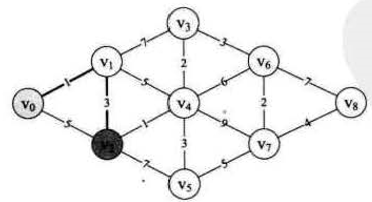
然后发现和 v2 邻接的点有 v4 、v5,v2 → v4 = 1,v2 → v5 = 7,可知 v2 → v4 最近,而之前通往 v4 的路径有 v0 → v1 → v4 = 6,而现在的 v0 → v1 → v2 → v4 = 5, 5 < 6 ,比较之下选择后者然后
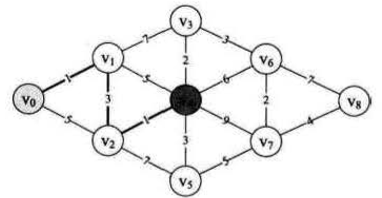
最短路径拓展到 v4 ,扫描周围顶点,v3 、v6 、v7 、v5,属 v3 权值最小,v0 → v1 → v2 → v4 → v3 = 7 ,而扫描之前能够到达 v3 的路径,v0 → v1 → v3 = 8 ,故应选择前者,最短路径扩展到 v3
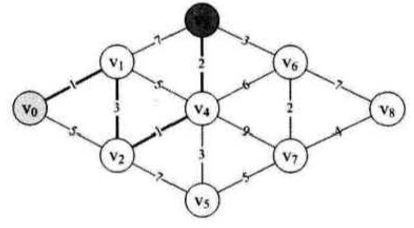
相信到这里你也大致了解了迪杰斯特拉寻找最短路径的方法,我们来总结一下,首先初始化源点,然后扫描和源点有权值连线的顶点,寻找最小权值的点进行联谊,而进行到后期要进行的工作还包括和之前的路径进行比较,因为很有可能之前的路径总权值要小于现在执行到的这个点。
下面我们来看一下代码:(这里就不进行图的结构定义了,可以参照前面的文章)
1 #define MAXVEX 9 2 #define INFINITY 65535 3 typedef int Pathmatirx[MAXVEX];//用来储存最短路径下标的数组 4 typedef int ShortPathTable[MAXVEX];//用来储存到每一个顶点最短路径值得数组 5 void ShortestPath_Dijkstra(MGraph G,int v0,Pathmatirx *P,ShortPathTable *D) 6 { 7 /*初始化最短路径结构*/ 8 int v,w,k,min; 9 int final[MAXVEX]; 10 for(v = 0;v < G.numVertexes;v++) 11 { 12 final[v] = 0; 13 (*D)[v] = G.matirx[v0][v]; 14 (*P)[v] = 0; 15 } 16 (*D)[v0] = 0; 17 final[v0] = 1; 18 /*实现最短路径主要循环*/ 19 for(v = 1;v < G.numVertexes;v++) 20 { 21 min = INFINITY; 22 for(w = 0;w < GnumVertexes;w++) 23 { 24 if(!final[w] && (*D)[w] < min) 25 { 26 k = w; 27 min = (*D)[w]; 28 } 29 } 30 final[k] = 1; 31 for(w = 0;w < G.numVertexes;w++) 32 { 33 if(!final[w] && (min + G.matirx[k][w] < (*D)[w])) 34 { 35 (*D)[w] = min + G.matirx[k][w]; 36 (*p)[w] = k; 37 } 38 } 39 } 40 }
我们用邻接矩阵的结构来实现 、且定义参数 v0 = 0:
- 8~17行系初始化各数据, final 数组用于标识是否加入最短路径,置 0 时为未加入,置 1 时表示该点已加入豪华最短路径,从后面得循环判断条件也可以得知。
- 第10行把数组中的每一个值都初始化为 0 ,表示所有顶点都还没有加入最短路径,13 行把源点 v0 的邻接情况输入了 D 数组中,而后16 、17行分别将 v0 → v0 的距离设为 0,和把 v0 设置为已经加入最短路径的状态,让之后的遍历不会涉及 v0 这个点,自此初始化完毕
- 19~39行为实现最短路径的循环,即每个顶点查找一遍,找到 v0 到每一个顶点的最短路径的前驱的下标和权值总和,分别储存在 P 和 D中
- 19~29行通过邻接矩阵中的一行来扫描一个点的临近所有权值连线,并且找到最小权值并用 k 存下标,然后置 final[k] 为1,表示这个点已经访问过并且加入最短路径,可以自己跟着这几行模拟一下找到 v1 的过程
- 31~38的循环是重头戏,看循环条件, !final[w] 表示 找未定的顶点, min + G.matirx[k][w] < (*D)[w] ,表示如果经过 w 下标的顶点如果权值小于现在的路径,则修改 D 和 P
下面看一下例子在实际循环中的各数值:
第一轮循环:初始化中,final[] = {1,0,0,0,0,0,0,0,0}, *D = {0,1,5,65535,65535,65535,65535,65535,65535} , *P = {0,0,0,0,0,0,0,0}
初始化结束,代码进入19行的循环,这时开始寻找 v0 身边权值最小路线对应的顶点,找到应该是 v1 ,这时 final[ ] = {1,1,0,0,0,0,0,0,0}
进入31行的循环,这时 只有 v0 、v1的 final 值为 1 ,寻到 v2 时,我们发现 这时 min = 1,而 v1 → v2 = 3 ,相加为4 小于 *D 的第二位5,这时呢,*D的第二位置 4 ,表示从 v0 → v2 的最小权值为 4 ,且置 *p 为 {0,0,1,0,0,0,0,0},循环还没完,因为 v1 与 v3 、v4都有一腿,最终循环完后,*D = {0,1,4,8,6,65535,65535,65535,65535} ,*p 为 {0,0,1,1,1,0,0,0,0},这是第一轮循环
第二轮循环:v0 、 v1已经不参与这次循环,故在 *D 中寻找,找到 4 ,即 v0 → v1 → v2 这条路,这时你应该发现刚才最后一步的妙用了,第一次的循环将v1的三条通路展示出来,此次遍历选出权值和为 4 的道路,且置 final[2] = 1 ,将 v2 加入最短路径,继续31行循环,*D = {0,1,4,8,5,11,65535,65535,65535},*p 为 {0,0,1,1,2,2,0,0,0},继续按照这种方式直到最后达到终点

其实最终返回的数组 D 和数组 P, 是可以得到 v0 到任意一个顶点的最短路径和路径长度的。例如 v0 到 v8 的最短路径并没有经过 v5,但我们已经知道 v0 到 v5 的最短路径了。由 D[5]=8 可知它的路径长度为 8 ,由 P[5]=4 可知 v5 的前驱顶点是 v4,所以 v0 到 v5 的最短路径是 v0 → v1 → v2 → v4 → v5 。