题目描述
有(n imes m)个人,排成一个(n imes m)的矩阵。每个同学和前后左右相邻的同学互相成为了好朋友。这学期要分文理科了,每个同学对于选择文科与理科有着自己的喜悦值,而一对好朋友如果能同时选文科或者理科,那么他们又将收获一些喜悦值。问全班喜悦值的和最大是多少。
(n,mleq 100)
题解
先把问题简化,考虑只有两个人,甲选文科的喜悦值为(a),甲选理科的喜悦值为(b),乙选文科的喜悦值为(c),乙选理科的喜悦值为(d),两人同时选文科的喜悦值为(e),两人同时选理科的喜悦值为(f)。
两个人同时选文或同时选理会有额外喜悦值,这并不太好处理。考虑转化一下。先把两人选文的喜悦值(a,c)加上两人同时选文科的喜悦值的一半(frac{e}{2})。如果只有一人选(即两人选的不同),那么就要减掉(frac{e}{2})。理科同理。
这样就是一个网络流的标准模型了。
最后拿(a+b+c+d+e+f)减掉最小割就是答案。
(e,f)有可能是奇数,可以把所有边的容量( imes 2),最后再除回来。
可以得到以下的网络:
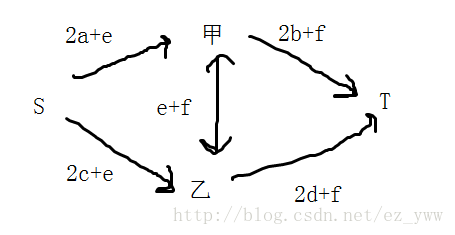
多个人的情况和两个人的情况类似,合在一起处理即可。
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cstdlib>
#include<ctime>
#include<utility>
#include<cmath>
#include<functional>
#include<queue>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair<int,int> pii;
typedef pair<ll,ll> pll;
void sort(int &a,int &b)
{
if(a>b)
swap(a,b);
}
void open(const char *s)
{
#ifndef ONLINE_JUDGE
char str[100];
sprintf(str,"%s.in",s);
freopen(str,"r",stdin);
sprintf(str,"%s.out",s);
freopen(str,"w",stdout);
#endif
}
int rd()
{
int s=0,c;
while((c=getchar())<'0'||c>'9');
do
{
s=s*10+c-'0';
}
while((c=getchar())>='0'&&c<='9');
return s;
}
int upmin(int &a,int b)
{
if(b<a)
{
a=b;
return 1;
}
return 0;
}
int upmax(int &a,int b)
{
if(b>a)
{
a=b;
return 1;
}
return 0;
}
int v[1000010];
int w[1000010];
int t[1000010];
int h[10010];
int cnt=0;
void add(int x,int y,int z)
{
cnt++;
v[cnt]=y;
w[cnt]=z;
t[cnt]=h[x];
h[x]=cnt;
}
int S,T;
int d[10010];
int e[10010];
int cur[10010];
int num;
int op(int x)
{
return ((x-1)^1)+1;
}
queue<int> q;
void bfs()
{
memset(d,-1,sizeof d);
memcpy(cur,h,sizeof h);
q.push(T);
d[T]=0;
int i,x;
while(!q.empty())
{
x=q.front();
q.pop();
e[d[x]]++;
for(i=h[x];i;i=t[i])
if(w[op(i)]&&d[v[i]]==-1)
{
d[v[i]]=d[x]+1;
q.push(v[i]);
}
}
}
int dfs(int x,int flow)
{
if(x==T)
return flow;
int s=0,c;
int &i=cur[x];
for(;i;i=t[i])
if(d[v[i]]==d[x]-1&&w[i])
{
c=dfs(v[i],min(flow,w[i]));
s+=c;
flow-=c;
w[i]-=c;
w[op(i)]+=c;
if(!flow)
return s;
}
e[d[x]]--;
if(!e[d[x]])
d[S]=num;
e[++d[x]]++;
cur[x]=h[x];
return s;
}
int maxflow()
{
bfs();
int ans=0;
while(d[S]<=num-1)
ans+=dfs(S,0x7fffffff);
return ans;
}
int m1[110][110];
int m2[110][110];
int m3[110][110];
int m4[110][110];
int m5[110][110];
int m6[110][110];
int n,m;
int id(int x,int y)
{
return (x-1)*m+y;
}
int a1[110][110];
int a2[110][110];
int a3[110][110];
int a4[110][110];
int main()
{
open("bzoj2127");
scanf("%d%d",&n,&m);
int i,j;
int sum=0;
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
{
scanf("%d",&m1[i][j]);
sum+=2*m1[i][j];
a1[i][j]+=2*m1[i][j];
}
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
{
scanf("%d",&m2[i][j]);
sum+=2*m2[i][j];
a2[i][j]+=2*m2[i][j];
}
for(i=1;i<n;i++)
for(j=1;j<=m;j++)
{
scanf("%d",&m3[i][j]);
sum+=2*m3[i][j];
a1[i][j]+=m3[i][j];
a1[i+1][j]+=m3[i][j];
a3[i][j]+=m3[i][j];
}
for(i=1;i<n;i++)
for(j=1;j<=m;j++)
{
scanf("%d",&m4[i][j]);
sum+=2*m4[i][j];
a2[i][j]+=m4[i][j];
a2[i+1][j]+=m4[i][j];
a3[i][j]+=m4[i][j];
}
for(i=1;i<=n;i++)
for(j=1;j<m;j++)
{
scanf("%d",&m5[i][j]);
sum+=2*m5[i][j];
a1[i][j]+=m5[i][j];
a1[i][j+1]+=m5[i][j];
a4[i][j]+=m5[i][j];
}
for(i=1;i<=n;i++)
for(j=1;j<m;j++)
{
scanf("%d",&m6[i][j]);
sum+=2*m6[i][j];
a2[i][j]+=m6[i][j];
a2[i][j+1]+=m6[i][j];
a4[i][j]+=m6[i][j];
}
num=n*m+2;
S=n*m+1;
T=n*m+2;
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
{
add(S,id(i,j),a1[i][j]);
add(id(i,j),S,0);
add(id(i,j),T,a2[i][j]);
add(T,id(i,j),0);
}
for(i=1;i<n;i++)
for(j=1;j<=m;j++)
{
add(id(i,j),id(i+1,j),a3[i][j]);
add(id(i+1,j),id(i,j),a3[i][j]);
}
for(i=1;i<=n;i++)
for(j=1;j<m;j++)
{
add(id(i,j),id(i,j+1),a4[i][j]);
add(id(i,j+1),id(i,j),a4[i][j]);
}
int ans=maxflow();
ans=sum-ans;
ans>>=1;
printf("%d
",ans);
return 0;
}