鉴于容易忘,决定先把目前会的写出来.....
莫比乌斯函数:
对于一个整数N,按照算数基本定理分解质因数为N = p1^c1 * p2^c2 * p3^c3 * ... * pm^cm
0 存在i∈[1, m],ci>1
μ(N) = { 1 m≡0(mod 2),任意i∈[1, m],ci = 1
-1 m≡1(mod 2),任意i∈[1, m],ci = 1
通俗讲:
①当N包含相等的质因子时,μ(N) = 0
②当N的所有质因子各不相等时,若N有偶数个质因子,μ(N) = 1
③当N有奇数个质因子时,μ(N) = -1
当然百度的话显然能找到更好的说明方式,但是我觉得这样比较清楚(虽然不利于理解求莫比乌斯函数)
莫比乌斯函数求法
1 memset(vis, 0, sizeof(vis));
2 miu[1] = 1, vis[1] = 1;
3 for(int i = 2; i < v; ++i) {
4 if(!vis[i]) prime[++cnt] = i, miu[i] = -1;
5 for(int j = 1; j <= cnt; ++j) {
6 if(prime[j] > v / i) break;
7 vis[i * prime[j]] = 1;
8 if(i % prime[j] == 0) {//说明对于i * prime[j], 其中prime[j]的幂大于1
9 miu[prime[j] * i] = 0;
10 break;
11 }
12 miu[prime[j] * i] = -miu[i];
13 }
14 }
莫比乌斯反演:
<1>莫比乌斯函数的一些性质:
·对于任意正整数n,Σμ(d) = [n=1] (d|n)
证明:当n = 1时,显然有函数g(n) = Σμ(d) = 1 (d|n)
当n = p^k时(p为质数)
g(n) = Σμ(d) = μ(1)+μ(p)+μ(p^2)+...+μ(p^k)
= 1 + (-1) + 0 + ... + 0 = 0
当n = p1^c1 * p2^c2 * ... * pk^ck时
g(n) = g(p1^c1)g(p2^c2)....g(pk^ck) = 0
·对于任意正整数n,Σμ(d)/d = φ(n)/n (d|n) //然而我并不会证明
<2>莫比乌斯反演
定理:F(n), f(n)为两个非负整数集合上的函数
F(n) = Σf(d) (d|n) <==> f(n) = ΣΣμ(d)*f(e) (前一个Σ范围为d|n,后一个Σ范围为e|(n/d))
证明:f(n)=Σμ(d)F(n/d) = Σμ(d)(d|n) * Σf(e)(e|(n/d)) = Σ(d|n)Σ(e|n/d)μ(d)*f(e)
交换求和顺序有:f(n) = Σf(e)(e|n)Σμ(d)(d|n/e)
根据莫比乌斯函数性质1,当且仅当n/e == 1,也就是n = e时,Σμ(d) = 1(d|n/e)
则f(n) = f(e)*1 = f(n)
证毕
(关于莫比乌斯反演,还有狄利克雷卷积证法,但是我不会.jpg)
莫比乌斯反演公式图片搬运版(因为我根本不会markdown语法)
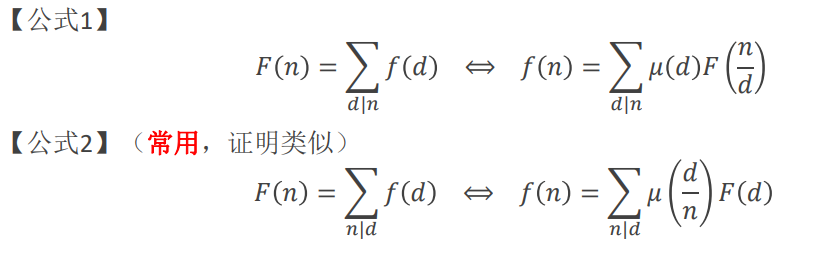
大佬眼中的入门题:
Bzoj2301
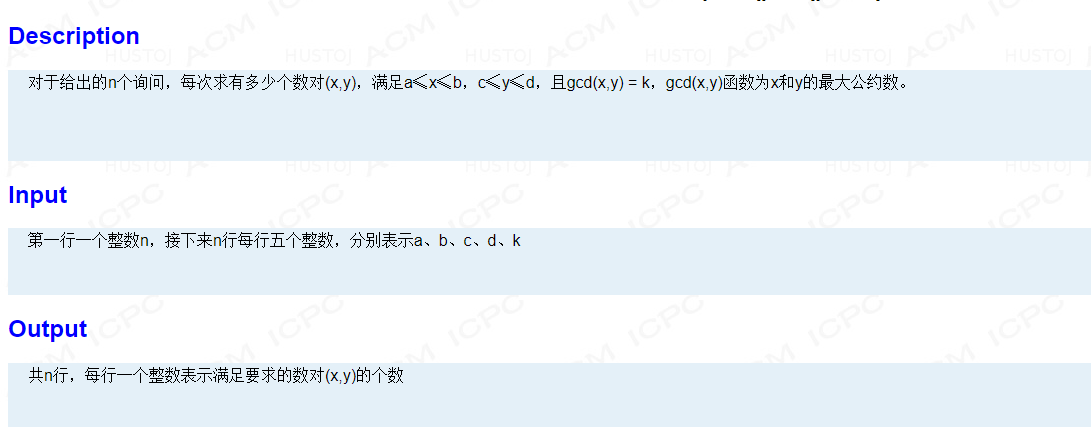
以cal(a, b, k)表示对于x<=a, y<=b,gcd(x, y)=k的x, y的对数
则我们求的是
ΣΣ[gcd(i,j)==k](1<=i<=n, 1<=j<=m)
则根据容斥原理,答案显然为
cal(b, d, k) - cal(a - 1, d, k) - cal(b, c - 1, k) + cal(a - 1, b - 1, k)
/*
对于问题ΣΣ[gcd(i,j)==k](1<=i<=n, 1<=j<=m),可以转化为
求对于1<=x<=[n/k],1<=y<=[m/k],gcd(x,y)互质的对数,也就是
ΣΣ[gcd(i,j)==1](1<=i<=[n/k], 1<=j<=[m/k])
实际上莫比乌斯反演式的本质就是Σμ(d)=[n==1] (d|n)
因此有Σμ(d)=[gcd(i,j)==1] (d|gcd(i,j))
因此也就是求
ΣΣΣμ(d) (1<=i<=[n/k], 1<=j<=[m/k], d|gcd(i,j))
.....
这些是另一个常见推法的基本操作,但是我不会和式变换所以我不会这么推....
*/
f(i)表示1<=x<=n, 1<=y<=m, 且gcd(x,y)=i的数对(x,y)的个数
F(i)表示1<=x<=n, 1<=y<=m, 且i|gcd(x,y)的数对(x,y)的个数
则F(i)=[n/i]*[m/i],
F[i]=Σf(d)(d|i)
→f(i)=Σμ(d/i)F(d) (i|d)
→f(i)=Σμ(d/i)[n/d][m/d] (i|d)
对于题目,我们只需要求f(k),然后枚举d(d为k的倍数)
也就是枚举k的每一个倍数可以在O(n)复杂度内回答一次询问,显然不能通过题目
考虑优化,容易注意到:我们对于k的倍数的枚举取决于[n/d]和[m/d]的取值
首先分析[n/d]的取值
1)当1<=d<=[sqrt(n)]时,最多有[sqrt(n)]种不同的取值
2)当[sqrt(n)]+1<=d<=n是,由于[n/d]<=[sqrt(n)],因此有[sqrt(n)]种不同的取值
综上所述+同理:
[n/d]有2[sqrt(n)]种不同的取值
[m/d]有2[sqrt(m)]种不同的取值
那么[n/d][m/d]有多少种不同的取值呢
首先,不是4[sqrt(n)][sqrt(m)]个
考虑在一个数轴上,[n/d]将一段变成了2[sqrt(n)]个块,每个块内取值相同,表示有2[sqrt(n)]中取值
同理考虑[m/d],然后手画一个图,可以发现,对于[n/d]划出的块和[m/d]划出的块的间断点是不同的
将[n/d]和[m/d]合并,其实是间断点的合并,即:块的数量变为了2[sqrt(n)]+2[sqrt(m)]
也就是说[n/d][m/d]一共有2[sqrt(n)]+2[sqrt(m)]个取值
对莫比乌斯函数维护前缀和,对于每一段就可以直接回答了
令n <= m这样对于每次询问,复杂度为O(sqrt(n))
总复杂度就是O(q*sqrt(n))
1 #include<bits/stdc++.h>
2 #define ll long long
3 #define uint unsigned int
4 #define ull unsigned long long
5 using namespace std;
6 const int maxn = 50010;
7 int miu[maxn], sum_miu[maxn];
8 int T, a, b, c, d, k, cnt = 0;
9 int prime[maxn], vis[maxn];
10
11 inline int read() {
12 int x = 0, y = 1;
13 char ch = getchar();
14 while(!isdigit(ch)) {
15 if(ch == '-') y = -1;
16 ch = getchar();
17 }
18 while(isdigit(ch)) {
19 x = (x << 1) + (x << 3) + ch - '0';
20 ch = getchar();
21 }
22 return x * y;
23 }
24
25 inline void pre_miu(int v) {
26 memset(vis, 0, sizeof(vis));
27 miu[1] = 1, vis[1] = 1;
28 for(int i = 2; i < v; ++i) {
29 if(!vis[i]) prime[++cnt] = i, miu[i] = -1;
30 for(int j = 1; j <= cnt; ++j) {
31 if(prime[j] > v / i) break;
32 vis[i * prime[j]] = 1;
33 if(i % prime[j] == 0) {//说明对于i * prime[j], 其中prime[j]的幂大于1
34 miu[prime[j] * i] = 0;
35 break;
36 }
37 miu[prime[j] * i] = -miu[i];
38 }
39 }
40 for(int i = 2; i < v; ++i) miu[i] += miu[i - 1];
41 }
42
43 inline ll calc(int n, int m, int k) {//枚举不同的值,last指向下一个间断点,这个方法又被称为数论分块
44 n /= k, m /= k;
45 if(n > m) swap(n, m);
46 int last = 0; ll res = 0;
47 for(int i = 1; i <= n; i = last + 1) {
48 last = min(n / (n / i), m / (m / i));
49 res += 1LL * (n / i) * (m / i) * (miu[last] - miu[i - 1]);
50 }
51 return res;
52 }
53
54 int main() {
55 T = read();
56 pre_miu(maxn);
57 while(T--) {
58 a = read(), b = read(), c = read(), d = read(), k = read();
59 ll ans = calc(b, d, k) - calc(a - 1, d, k) - calc(b, c - 1, k) + calc(a - 1, c - 1, k);
60 printf("%lld
", ans);
61 }
62 return 0;
63 }
后续的题目回头慢慢补咕咕咕....
Bzoj4804欧拉心算
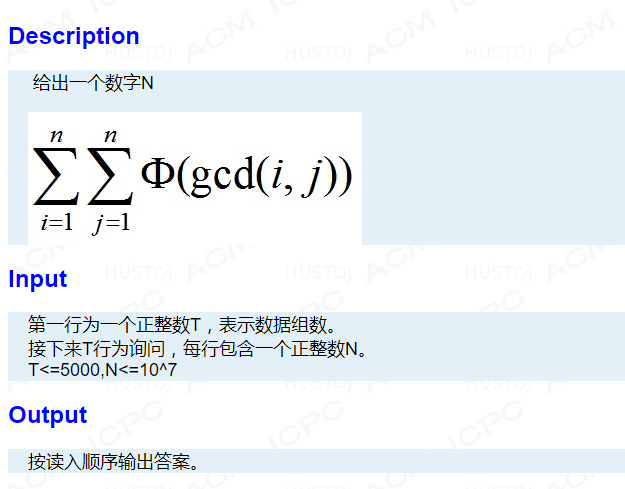
对于AC此题,需要推式子(1)
关于此题的解法是如何想到的,我只能说我也是看课件(题解)的.....(2)
式子推的乱不要慌张,毕竟我不会markdown(3)
关于Σ的范围和对应的字母,看我后面括号里的顺序确定吧......(4)
对于式子ΣΣφ(gcd(i,j)) (1<=i<=n, 1<=j<=n),我们令d = gcd(i, j)
可得ΣΣφ(d) (1<=i<=n, i<=j<=n),我们进行和式变换,先枚举d,可得:
Σφ(d) ΣΣ[gcd(i, j) == d] (1<=d<=n , 1<=i<=n , 1<=j<=n)
==> Σφ(d) ΣΣ[gcd(i, j) == 1] (1<=d<=n , 1<=i<=[n/d] , 1<=j<=[n/d]) //注:此处以及以下的[x/y]形式的都表示下取整,(貌似数学内的取证符号就是下取整??(不清楚))
==> Σφ(d) Σμ(i)([n/(d*i)]^2) (1<=d<=n , 1<=i<=[n/d]) //关于这一步如何推得?就是对后面两个Σ进行反演
令D = d*i, 和式变换得:
==> Σ([n/D]^2) Σφ(d)μ(D/d) (1<=D<=n, d|D) //关于这一步如何推得?改变枚举顺序,将未知数只含D的项提出去,因为D=d*i,因此D∈[1, n],然后i用D/d表示,d的范围就是d|D
这样,接下来的问题转变为筛Σφ(d)μ(D/d) (d|D),观察/打表/证明/猜想(或是看题解)可知这是一个积性函数
令h(d) = Σφ(d)μ(D/d) (d|D),考虑分类讨论:设p为一个质数
1) h(p) = φ(1)μ(p) + φ(p)μ(1) = -1 + p - 1 = p - 2
2) h(p^2) = φ(1)μ(p^2) + φ(p)μ(p) + φ(p^2)μ(1) = p^2 - 2p + 1 = (p - 1)^2
3) h(p^k) = φ(1)μ(p^k) + φ(p)μ(p^(k-1)) + ...... + φ(p^(k-1))μ(p) + φ(p^k)μ(1) = p^(k-1) (p-1) - p^(k-2) (p-1)
= p^(k-2) (p-1)^2 = p^(k-2) h(p^2) = ph(p^k-1) //由此可以得到一个递推式,设h(p^i), 则h(p^i) = h(p^(i-1))*p
4)gcd(a, p) = 1, 则根据积性函数, h(ap) = h(a)*h(p)
其余情况根据积性函数推即可
1 #include<bits/stdc++.h>
2 #define ll long long
3 #define uint unsigned int
4 #define ull unsigned long long
5 using namespace std;
6 const int maxn = 1e7+10;
7 int miu[maxn], prime[maxn];
8 bool vis[maxn];
9 int T, n, tot = 0;
10 int h[maxn];
11 ll sum_h[maxn];
12
13 inline int read() {
14 int x = 0, y = 1;
15 char ch = getchar();
16 while(!isdigit(ch)) {
17 if(ch == '-') y = -1;
18 ch = getchar();
19 }
20 while(isdigit(ch)) {
21 x = (x << 1) + (x << 3) + ch - '0';
22 ch = getchar();
23 }
24 return x * y;
25 }
26
27 inline void Mobius(int v) {
28 memset(vis, 0, sizeof(vis));
29 h[1] = 1, vis[1] = 1;
30 for(int i = 2; i <= v; ++i) {
31 if(!vis[i]) {
32 vis[i] = 1;
33 prime[++tot] = i, h[i] = i - 2;
34 }
35 for(int j = 1; j <= tot; ++j) {
36 if(prime[j] > v / i) break;
37 vis[i * prime[j]] = 1;
38 if(i % prime[j] == 0) {
39 if((i / prime[j]) % prime[j] == 0)
40 h[i * prime[j]] = h[i] * prime[j];
41 else h[i * prime[j]] = h[i / prime[j]] * (prime[j] - 1) * (prime[j] - 1);
42 //对于else 设i = ap, 则h(i*p) = h(ap^2) = h(a) * h(p^2),以及p^2 h(p^2) = 1 * (p-1)^2
43 break;
44 }
45 h[i * prime[j]] = h[i] * h[prime[j]];//无特殊情况时,就是积性函数
46 }
47 }
48 for(int i = 1; i <= v; ++i) sum_h[i] = sum_h[i - 1] + h[i];
49 }
50
51 int main() {
52 Mobius(maxn);
53 T = read();
54 while(T--) {
55 n = read();
56 ll ans = 0;
57 for(int i = 1, last; i <= n; i = last + 1) {
58 last = n / (n / i);
59 ans += 1LL * (n / i) * (n / i) * (sum_h[last] - sum_h[i - 1]);
60 }
61 printf("%lld
", ans);
62 }
63 return 0;
64 }