题目链接:传送门
题目大意:
对于给定的非负整数n,返回一个长度位$2^n$序列
要求:
- 相邻两个数的位数仅有一位差距
- 所有数字不相同
- 第一个数字位0
解法一:(虚假的解法
class Solution {
public:
vector<int> grayCode(int n) {
vector<int> ans;
ans.push_back(0);
//遍历位数
for(int i = 0;i < n;i++){
//取前一次长度遍历
for(int j = ans.size() - 1;j >= 0;j--){
//每次添加ans[j] ^ ( 1 << i),即令当前遍历位数的bit为1
ans.push_back(ans[j] ^ (1 << i));
}
}
return ans;
}
};
// 0000 0001 0011 0010 0110 0111 0101 0100
上面的解法并不困难,且容易理解。
解法二
此解法我理解不深刻,有错误之处还请指正。
List<Integer> list = new ArrayList<>();
for(int i = 0;i < 1 << n;i++){
ans.add(i ^ i >> 1);
}
return ans;
先证明相邻两数只差一位
$$
x otimes (x >> 1) ^ ((x + 1) otimes ((x + 1) >> 1))
= [x otimes (x + 1)] otimes [(x >> 1) otimes ((x + 1) >> 1)]
$$
因此先计算$$x otimes (x + 1) $$,不妨计算过程为下面的形式
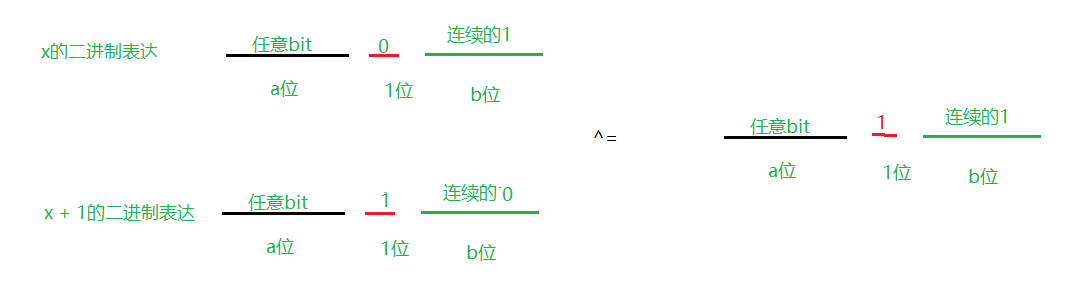
同理另一半的值以为向右移动一位应该为下面的形式
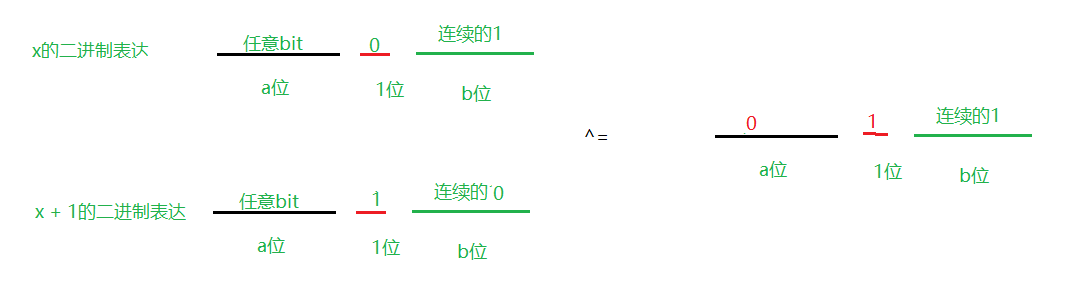
很明显可以知道最终的计算结果应该为
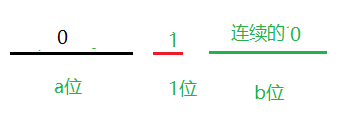
最终我们得到到了相邻两个数值差这一位。
而这些证明并不能代表我们的题解是正确的,还需要证明这$1 << n$个数完全不相等
考虑这样的事:当n == 3时,我们已经有
0 , 1, 3, 2
那么后买你4个数如和添加的呢,此时题解中的$i == 4$那么$ i otimes (i >> 1)$应该保留第一位的1,并且
$$
(x + 1) otimes ((x + 1) >> 1)
= x otimes ( x >> 1) otimes (x的最低一位0)
$$
一旦$x$跨越$x^i - 1$的时候那么 $x otimes (x >> 1)$一定会保证最高一位是1,更细节一点的证明我想不出来了
算证明了3/4吧