题目描述
给定不同面额的硬币 coins 和一个总金额 amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回 -1。
示例 1:
输入: coins = [1, 2, 5], amount = 11
输出: 3
解释: 11 = 5 + 5 + 1
示例 2:
输入: coins = [2], amount = 3
输出: -1
解题思路
-
自顶向下找一下规律
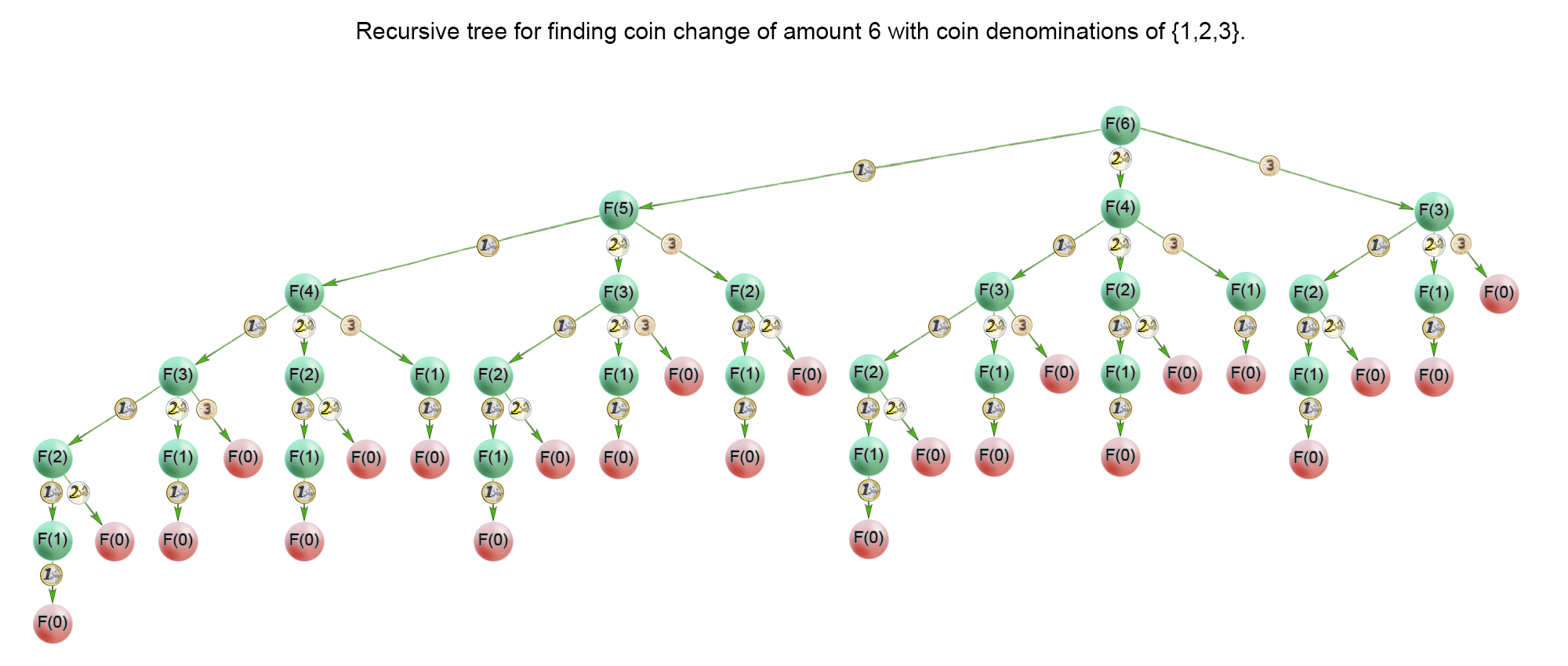
-
状态转移方程
F(i) = min{F(i - c_j)} + 1,j = 0...n-1 -
自底向上解决问题
其中 F(0) = 0
Java 实现
public int coinChange (int[] coins, int amount) {
int[] dp = new int[amount + 1];
Arrays.fill(dp, amount + 1);
dp[0] = 0;
for (int i = 1; i <= amount; i++) {
for (int coin : coins) {
if (coin <= i) {
dp[i] = Math.min(dp[i], dp[i - coin] + 1);
}
}
}
return dp[amount] > amount ? -1 : dp[amount];
}
心得体会
这是一道典型的动态规划的题目。先自顶向下找到规律,再通过状态转移方程描述这个规律,最后使用自底向上简化时间复杂度。