题目描述
根据一棵树的前序遍历与中序遍历构造二叉树。
注意:
你可以假设树中没有重复的元素。
例如,给出
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树:
3
/
9 20
/
15 7
解题思路
首先列举一下二叉树的三种常见遍历方式:
- 前序遍历:根 - 左 - 右
- 中序遍历:左 - 根 - 右
- 后序遍历:左 - 右 - 根
可以发现,「前中后」是指根节点在三个节点中的相对顺序。
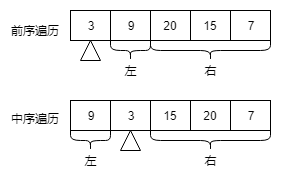
根据二叉树遍历的特点,前序遍历的第一个节点一定是整棵二叉树的根节点,根据这一特点找到根节点,新建一棵二叉树。找到根节点后,在中序遍历的序列中找到根节点的值对应的位置,以这个节点为界,左边是根节点的左子树,右边是根节点的右子树。最后利用递归的方法,构造起整棵二叉树。
具体实现
我们需要一个辅助函数
private TreeNode help(int startPre, int startIn,int endIn,int[] preorder, int[] inorder)
其中:
int satrtPre用来在前序遍历序列中定位根节点int startIn用来在中序遍历序列中定位左子树的起点(终点取决于根节点在中序遍历序列中的位置)int endIn用来在中序遍历序列中定位右子树的终点(起点取决于根节点在中序遍历序列中的位置)
此外,在每次迭代中,都要更新当前根节点在对应的中序遍历序列中的索引,用int curInIndex表示
源代码
public TreeNode buildTree (int[] preorder, int[] inorder) {
return help(0,0,inorder.length - 1,preorder,inorder);
}
private TreeNode help(int startPre, int startIn,int endIn,int[] preorder, int[] inorder) {
if (startPre > preorder.length - 1 || startIn > endIn) {
return null;
}
TreeNode root = new TreeNode(preorder[startPre]);
int curInIndex = 0; // 前根节点在对应的中序遍历序列中的索引
for (int i = startIn; i <= endIn; i++) {
if (root.val == inorder[i]) {
curInIndex = i;
}
}
root.left = help(startPre + 1,startIn,curInIndex - 1,preorder,inorder);
root.right = help(startPre + curInIndex - startIn + 1, curInIndex + 1, endIn, preorder, inorder);
return root;
}
心得体会
在二叉树的相关题目中,递归是很常用的一个方法,关键是找到递归的最小情况。现在掌握的还不熟练,需要多做一些树和链表相关的题目。