参考文献 :《信息奥赛一本通》,《算法竞赛进阶指南》
根据一位大佬模仿下排版....
介绍:
字典树也叫做Trie或者字母树,指的是某个字符串集合,如{AAA,AAG,T.TCA,TG}这样的
集合对应的形的有根树,用图片解释食用更香:
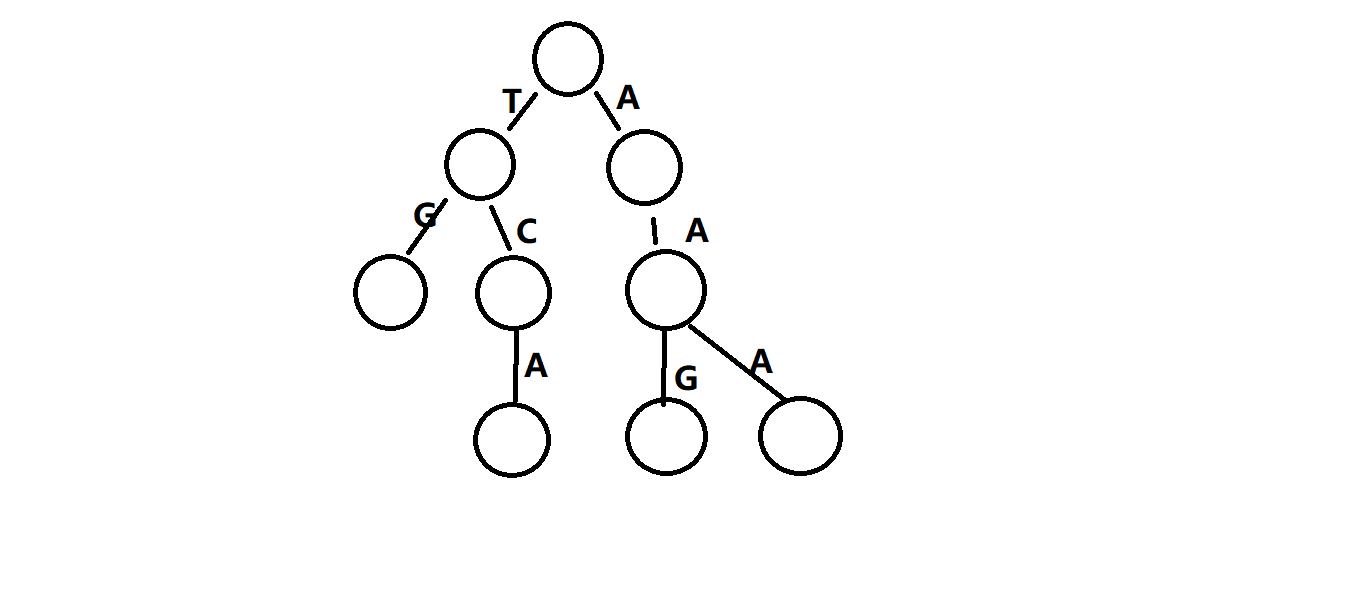
每个顶点代表从根到该节点所对应的字符串,就是从根到这个节点的子符全部串在一起,
所以我们也叫Trie上的边叫做转移,顶点为状态。
顶点上还能存储额外信息,如下
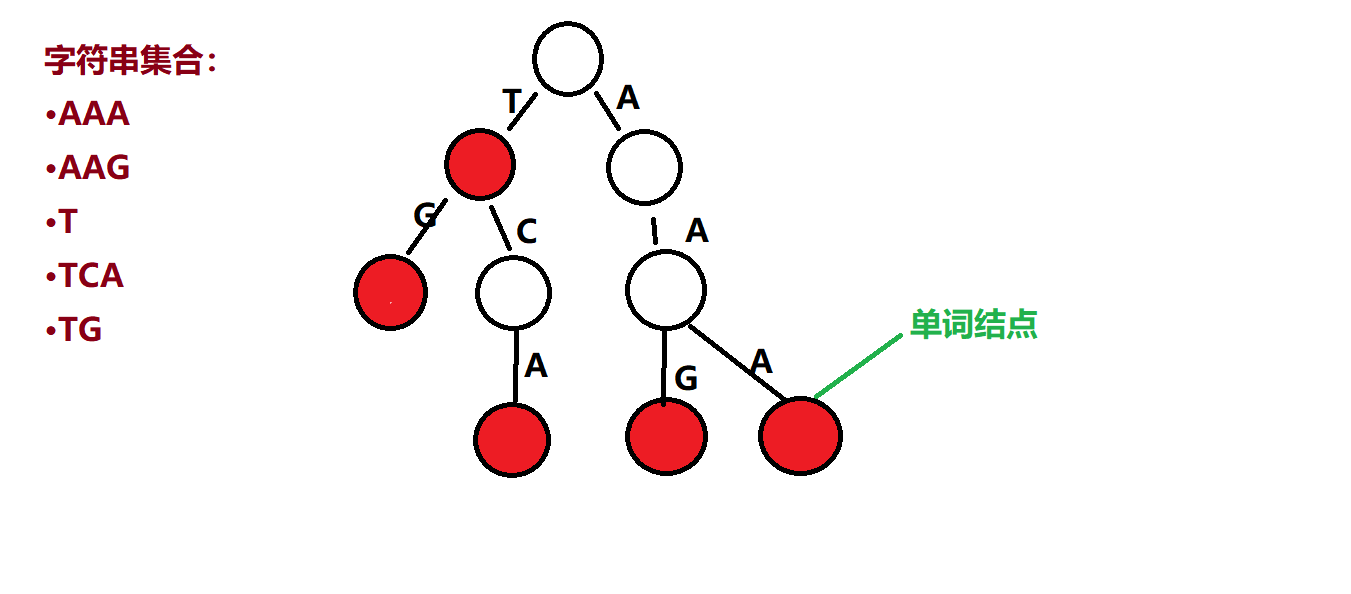
这些从根到这些标红点组成的字符串都是集合中的元素,所以叫他们为单词节点(结==节,懒得改了)
还有,任意一个线节点代表的字符串,都是这些实际字符串中某些串的前缀。specially,根节点表示空串。
任意一节点,到子节点边上字符都不同,这就是利用了串的公共前缀,如TG与TCA公共前缀为T....
本质上它就是通过空间去换取时间。
操作
1.初始化:
一棵空的Trie只剩下一个根节点,它的字符指针指向空,显然。
2.插入操作
当我们需要插入一个字符串s时,我们让一个指针P先指向根节点,然后依次扫描s中的每个字符x:
若P的x字符指针指向一个已经存在的节点A,则让P = A;
若P的x字符指针指向空,就是原来不存在这个字符的连接节点,那就得给它构造一个节点,再让P的x字符指针指向A,最后让P=A;
当s字符全部扫描完毕,就在当前节点P标记它是末尾。
long trie[MAXN][26],tot=1;//初始化,且假定字符串全
bool end[MAXN]; //由小写字母构成
inline void insert(char* s){
long len=strlen(s),p=1;
for(long i=0;i<len;i++){
long ch=s[i]-'a';
if(trie[p][ch]==0) trie[p][ch]=++tot;
p=trie[p][ch];
}
end[p]=1;
}
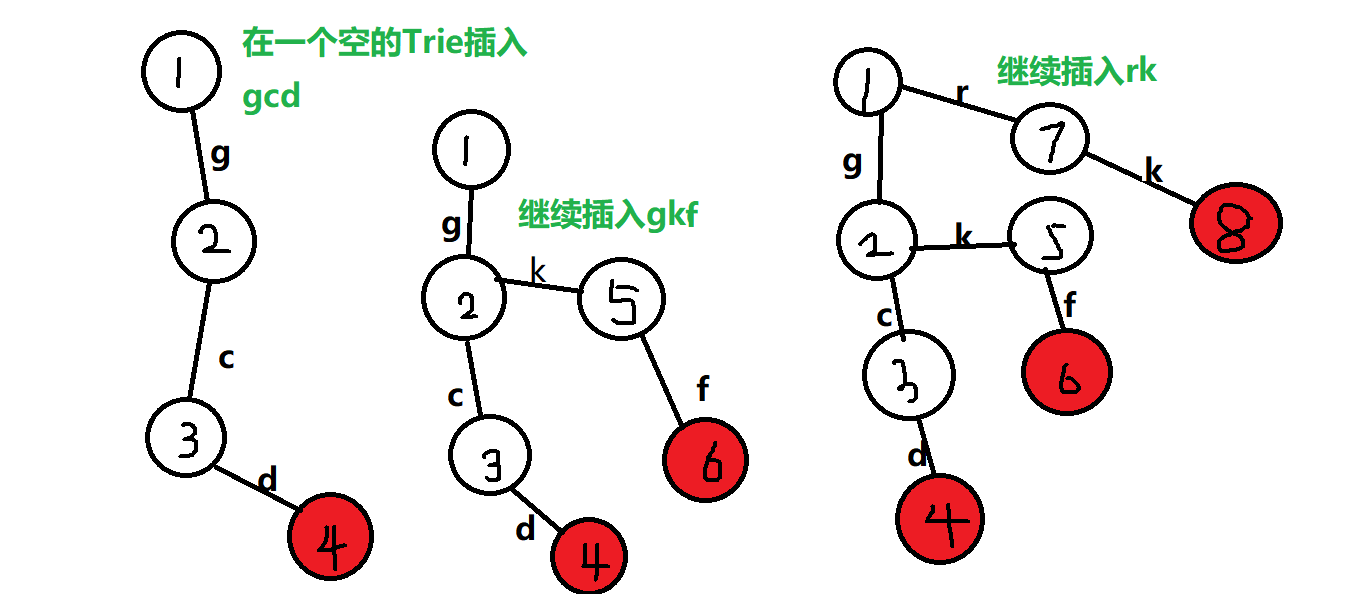
3.查询操作
当我们需要查询时,我们就先让一个指针P指向根结点,再依次扫描s中每一个字符x:
若P的x字符指针指向空,那就是没找到嘛,所以就干脆不找下去了,前缀都不一样找下去没啥意思。
若P的x字符指针指向一个已经存在的节点A,那就是还能有,于是让P=A;
当s扫描一遍后,若发现当前P被标记在一个字符串的末尾,则说明s是在这棵字典树是存在的,反之则说明s没在里面。
bool search(char* s){
long len=strlen(s),p=1;
for(long i=0;i<len;i++){
p=trie[p][s[i]-'a'];
if(p==0) return 0;//只要指向下一个为空,那就是没有了
}
reuturn end[p];//不能直接判1,因为可能这只是某个字
//符串的前缀而已
}
~~~字符数据都体现在边上,节点只是保留额外信息,空间复杂度为O(NC),N为节点数,C为字符集大小。
其余的只能多刷刷题
kmp和trie只是为了给AC自动机打基础