损失函数是模型优化的目标,用于衡量在无数的参数取值中,哪一个是最理想的。损失函数的计算在训练过程的代码中,每一轮的训练代码均是一致的过程:先根据输入数据正向计算预测输出,再根据预测值和真实值计算损失,最后根据损失反向传播梯度并更新参数。
在之前的方案中,我们照抄了房价预测模型的损失函数-均方误差。虽然从预测效果来看,使用均方误差使得损失不断下降,模型的预测值逐渐逼近真实值,但模型的最终效果不够理想。原因是不同的机器学习任务有各自适宜的损失函数。房价预测是回归任务,而手写数字识别属于分类任务。分类任务中使用均方误差作为损失存在逻辑和效果上的缺欠,比如房价可以是0-9之间的任何浮点数,手写数字识别的数字只可能是0-9之间的10个实数值(标签)。
在房价预测的案例中,因为房价本身是一个连续的实数值,以模型输出的数值和真实房价差距作为损失函数(loss)是符合道理的。但对于分类问题,真实结果是标签,而模型输出是实数值,导致两者相减的物理含义缺失。如果模型能输出十个标签的概率,对应真实标签的概率输出尽可能接近100%,而其他标签的概率输出尽可能接近0%,且所有输出概率之和为1。这是一种更合理的假设!与此对应,真实的标签值可以转变成一个10维度的one-hot向量,在对应数字的位置上为1,其余位置为0,比如标签“6”可以转变成[0,0,0,0,0,1,0,0,0,0]。
为了实现上述假设,需要引入Softmax函数。它可以将原始输出转变成对应标签的概率,公式如下。
softmax(xi)=exi / Sigmae j x(j=0-N,i=0,1,...c-1)
C是标签类别个数。 从公式的形式可见,每个输出的范围均在0~1之间,且所有输出之和等于1,这是这种变换后可被解释成概率的基本前提。对应到代码上,我们需要在网络定义部分修改输出层:self.fc = FC(name_scope, size=10, act='softmax'),即是对全连接层FC的输出加一个softmax运算。
在该假设下,采用均方误差衡量两个概率的差别不是理论上最优的。人们习惯使用交叉熵误差作为分类问题的损失衡量,因为后者有更合理的物理解释,详见《机器学习的思考故事》。
交叉熵的公式
L=-[ Sigma tk logyk + (1-yk) log(1-yk) ]
其中,log表示以e为底数的自然对数。yk代表模型输出,tk代表各个标签。tk中只有正确解的标签为1,其余均为0(one-hot表示)。因此,交叉熵只计算对应着“正确解”标签的输出的自然对数。比如,假设正确标签的索引是“2”,与之对应的神经网络的输出是0.6,则交叉熵误差是−log0.6=0.51;若“2”对应的输出是0.1,则交叉熵误差为−log0.1=2.30。由此可见,交叉熵误差的值是由正确标签所对应的输出结果决定的。
自然对数的函数曲线可由如下代码显示。
1 import matplotlib.pyplot as plt 2 import numpy as np 3 x = np.arange(0.01,1,0.01) 4 y = np.log(x) 5 plt.title("y=log(x)") 6 plt.xlabel("x") 7 plt.ylabel("y") 8 plt.plot(x,y) 9 plt.show() 10 plt.figure()
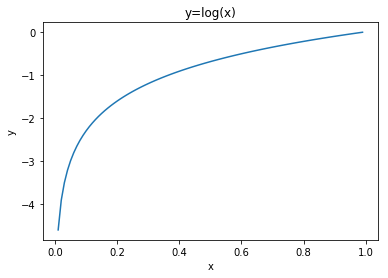
如自然对数的图形所示,当x等于1时,y为0;随着x向0靠近,y逐渐变小。因此,正确解标签对应的输出越大,交叉熵的值越接近0,对应loss越小;当输出为1时,交叉熵误差为0。反之,如果正确解标签对应的输出越小,则交叉熵的值越大,对应loss越大。
在手写数字识别任务中,如果在现有代码中将模型的损失函数替换成交叉熵(cross_entropy),仅改动三行代码即可:在读取数据部分,将标签的类型设置成int,体现它是一个标签而不是实数值(飞桨框架默认将标签处理成int64);在网络定义部分,将输出层改成“输出十个标签的概率”的模式;以及在训练过程部分,将损失函数从均方误差换成交叉熵。
- 数据处理部分:label = np.reshape(labels[i], [1]).astype('int64')
- 网络定义部分:self.fc = FC(name_scope, size=10, act='softmax')
- 训练过程部分:loss = fluid.layers.cross_entropy(predict, label)
如下是在数据处理部分,修改标签变量Label的格式。
- 从:label = np.reshape(labels[i], [1]).astype('float32')
- 到:label = np.reshape(labels[i], [1]).astype('int64')
1 #修改标签数据的格式,从float32到int64 2 import os 3 import random 4 import paddle 5 import paddle.fluid as fluid 6 from paddle.fluid.dygraph.nn import Conv2D, Pool2D, FC 7 import numpy as np 8 from PIL import Image 9 10 import gzip 11 import json 12 13 # 定义数据集读取器 14 def load_data(mode='train'): 15 16 # 数据文件 17 datafile = './work/mnist.json.gz' 18 print('loading mnist dataset from {} ......'.format(datafile)) 19 data = json.load(gzip.open(datafile)) 20 train_set, val_set, eval_set = data 21 22 # 数据集相关参数,图片高度IMG_ROWS, 图片宽度IMG_COLS 23 IMG_ROWS = 28 24 IMG_COLS = 28 25 26 if mode == 'train': 27 imgs = train_set[0] 28 labels = train_set[1] 29 elif mode == 'valid': 30 imgs = val_set[0] 31 labels = val_set[1] 32 elif mode == 'eval': 33 imgs = eval_set[0] 34 labels = eval_set[1] 35 36 imgs_length = len(imgs) 37 38 assert len(imgs) == len(labels), 39 "length of train_imgs({}) should be the same as train_labels({})".format( 40 len(imgs), len(labels)) 41 42 index_list = list(range(imgs_length)) 43 44 # 读入数据时用到的batchsize 45 BATCHSIZE = 100 46 47 # 定义数据生成器 48 def data_generator(): 49 if mode == 'train': 50 random.shuffle(index_list) 51 imgs_list = [] 52 labels_list = [] 53 for i in index_list: 54 img = np.reshape(imgs[i], [1, IMG_ROWS, IMG_COLS]).astype('float32') 55 label = np.reshape(labels[i], [1]).astype('int64') 56 imgs_list.append(img) 57 labels_list.append(label) 58 if len(imgs_list) == BATCHSIZE: 59 yield np.array(imgs_list), np.array(labels_list) 60 imgs_list = [] 61 labels_list = [] 62 63 # 如果剩余数据的数目小于BATCHSIZE, 64 # 则剩余数据一起构成一个大小为len(imgs_list)的mini-batch 65 if len(imgs_list) > 0: 66 yield np.array(imgs_list), np.array(labels_list) 67 68 return data_generator
如下是在网络定义部分,修改输出层结构。
- 从:self.fc = FC(name_scope, size=1, act=None)
- 到:self.fc = FC(name_scope, size=10, act='softmax')
1 # 定义模型结构 2 class MNIST(fluid.dygraph.Layer): 3 def __init__(self, name_scope): 4 super(MNIST, self).__init__(name_scope) 5 name_scope = self.full_name() 6 # 定义一个卷积层,使用relu激活函数 7 self.conv1 = Conv2D(name_scope, num_filters=20, filter_size=5, stride=1, padding=2, act='relu') 8 # 定义一个池化层,池化核为2,步长为2,使用最大池化方式 9 self.pool1 = Pool2D(name_scope, pool_size=2, pool_stride=2, pool_type='max') 10 # 定义一个卷积层,使用relu激活函数 11 self.conv2 = Conv2D(name_scope, num_filters=20, filter_size=5, stride=1, padding=2, act='relu') 12 # 定义一个池化层,池化核为2,步长为2,使用最大池化方式 13 self.pool2 = Pool2D(name_scope, pool_size=2, pool_stride=2, pool_type='max') 14 # 定义一个全连接层,输出节点数为10 15 self.fc = FC(name_scope, size=10, act='softmax') 16 # 定义网络的前向计算过程 17 def forward(self, inputs): 18 x = self.conv1(inputs) 19 x = self.pool1(x) 20 x = self.conv2(x) 21 x = self.pool2(x) 22 x = self.fc(x) 23 return x
如下代码仅修改计算损失的函数,从均方误差(常用于回归问题)到交叉熵误差(常用于分类问题)。
- 从:loss = fluid.layers.square_error_cost(predict, label)
- 到:loss = fluid.layers.cross_entropy(predict, label)
1 #仅修改计算损失的函数,从均方误差(常用于回归问题)到交叉熵误差(常用于分类问题) 2 with fluid.dygraph.guard(): 3 model = MNIST("mnist") 4 model.train() 5 #调用加载数据的函数 6 train_loader = load_data('train') 7 optimizer = fluid.optimizer.SGDOptimizer(learning_rate=0.01) 8 EPOCH_NUM = 5 9 for epoch_id in range(EPOCH_NUM): 10 for batch_id, data in enumerate(train_loader()): 11 #准备数据,变得更加简洁 12 image_data, label_data = data 13 image = fluid.dygraph.to_variable(image_data) 14 label = fluid.dygraph.to_variable(label_data) 15 16 #前向计算的过程 17 predict = model(image) 18 19 #计算损失,使用交叉熵损失函数,取一个批次样本损失的平均值 20 loss = fluid.layers.cross_entropy(predict, label) 21 avg_loss = fluid.layers.mean(loss) 22 23 #每训练了200批次的数据,打印下当前Loss的情况 24 if batch_id % 200 == 0: 25 print("epoch: {}, batch: {}, loss is: {}".format(epoch_id, batch_id, avg_loss.numpy())) 26 27 #后向传播,更新参数的过程 28 avg_loss.backward() 29 optimizer.minimize(avg_loss) 30 model.clear_gradients() 31 32 #保存模型参数 33 fluid.save_dygraph(model.state_dict(), 'mnist')
loading mnist dataset from ./work/mnist.json.gz ...... epoch: 0, batch: 0, loss is: [2.609301] epoch: 0, batch: 200, loss is: [0.36067933] epoch: 0, batch: 400, loss is: [0.3503476] epoch: 1, batch: 0, loss is: [0.29702342] epoch: 1, batch: 200, loss is: [0.15377608] epoch: 1, batch: 400, loss is: [0.1849378] epoch: 2, batch: 0, loss is: [0.08589315] epoch: 2, batch: 200, loss is: [0.10543882] epoch: 2, batch: 400, loss is: [0.07615029] epoch: 3, batch: 0, loss is: [0.1301367] epoch: 3, batch: 200, loss is: [0.17038517] epoch: 3, batch: 400, loss is: [0.13615657] epoch: 4, batch: 0, loss is: [0.16349195] epoch: 4, batch: 200, loss is: [0.1656445] epoch: 4, batch: 400, loss is: [0.06402704]
虽然上述训练过程的损失明显比使用均方误差算法要小,但因为损失函数量纲的变化,我们无法从比较两个不同的Loss得出谁更加优秀。怎么解决这个问题呢?我们可以回归到问题的直接衡量,谁的分类准确率高来判断。
因为我们修改了模型的输出格式,所以使用模型做预测时的代码也需要做相应的调整。从模型输出10个标签的概率中选择最大的,将其标签编号输出。
1 # 读取一张本地的样例图片,转变成模型输入的格式 2 def load_image(img_path): 3 # 从img_path中读取图像,并转为灰度图 4 im = Image.open(img_path).convert('L') 5 im.show() 6 im = im.resize((28, 28), Image.ANTIALIAS) 7 im = np.array(im).reshape(1, 1, 28, 28).astype(np.float32) 8 # 图像归一化 9 im = 1.0 - im / 255. 10 return im 11 12 # 定义预测过程 13 with fluid.dygraph.guard(): 14 model = MNIST("mnist") 15 params_file_path = 'mnist' 16 img_path = './work/example_0.jpg' 17 # 加载模型参数 18 model_dict, _ = fluid.load_dygraph("mnist") 19 model.load_dict(model_dict) 20 21 model.eval() 22 tensor_img = load_image(img_path) 23 #模型反馈10个分类标签的对应概率 24 results = model(fluid.dygraph.to_variable(tensor_img)) 25 #取概率最大的标签作为预测输出 26 lab = np.argsort(results.numpy()) 27 print("本次预测的数字是: ", lab[0][-1])
本次预测的数字是: 0