Leetcode刷题记录--22. 括号生成（回溯）

前言：今天又做了一道简单的括号生成，才发现自己上一次做回溯题的时候完全搞错了，回溯不等同于递归，回溯方法中会有一个全局变量保存当前的状态，当方法完成时，再回退回上一个状态。
数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

示例：

输入：n = 3
输出：[
"((()))",
"(()())",
"(())()",
"()(())",
"()()()"
]

这道题不算太难，我是用的pair去判断的最终状态，最终状态就是3个成对的串，不过其实这个条件可以换成其他更好的条件，还节省一个haspair的空间，比如说判断字符串的长度，或者判断左括号和右括号的数量是不是都成为了n
同时我用了回溯的思想，即开辟一个全局变量s，存放当前的字符串，但是要注意完成调用之后要回到上一个节点的状态，因此需要回退，在这题中通过删掉字符串最后一个字符实现。
大家可以借助这张图理解一下：

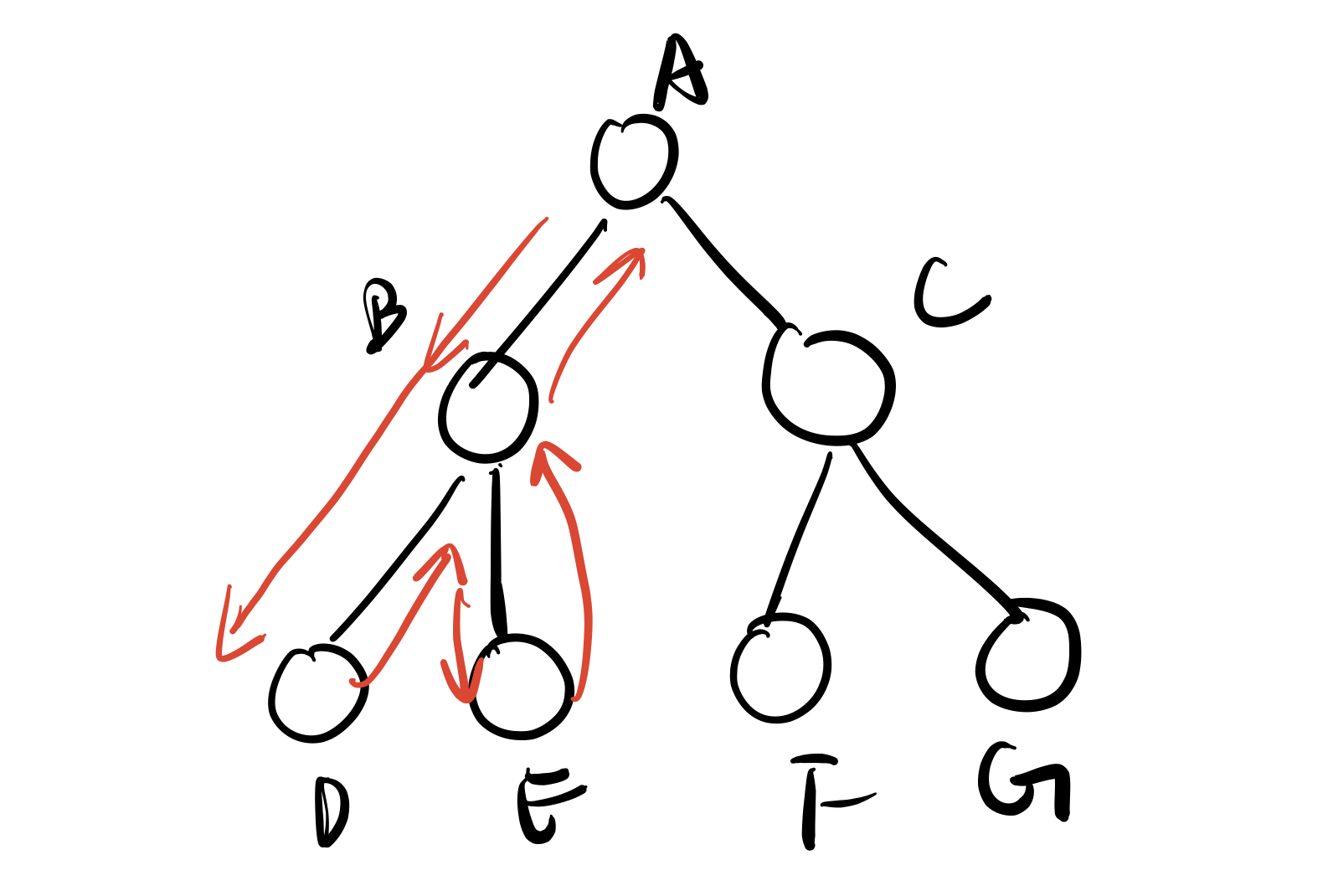
状态回退其实就是从D回到B的过程

具体实现代码如下：

class Solution {

string s ="";
public:
    vector<string> generateParenthesis(int n) {
        char symbol[2] = {'(',')'};
        vector<string> result;
        if(n == 0){
            result.push_back("");
            return result;
        }else{
            genSymbol(result, '(', 1, 0, 0, n);
            genSymbol(result, ')', 0, 1, 0, n);
            return result;
        }
        
    }


    void genSymbol(vector<string> &result, char symbol, int leftB, int rightB, int hasPair, int n ){
        
        if(hasPair == n){
            s += ')';
            result.push_back(s);
            s.pop_back();
            return;
        }else{
             s += symbol;
            if(leftB < n){
                // cout << s << " " << hasPair<< "   "<< leftB<<" " << rightB<< endl;
                genSymbol(result, '(', leftB+1, rightB, hasPair, n);
            }
            if(leftB > rightB){

                // cout << s << " " << hasPair+1<< "   "<< leftB<<" " << rightB<< endl;
               
                genSymbol(result, ')', leftB, rightB+1, hasPair+1, n);
               
            }
            
            s.pop_back();

        }
    }
};

内存消耗其实还是有优化的余地的~