这部分主要是学习一下计算 无法用内置整数类型来保存它的值(即位数多到long long都表示不了) 的整数的加法和乘法
这里使用的方法是首先读入到一个char的数组里,然后初始化转换到int数组里,这样一位就对应数组的一项。
那这里首先就要清楚,读如char的数组里它是怎么存储的,来看一个简单的代码
1 #include<stdio.h> 2 #include<stdlib.h> 3 #include<string.h> 4 int main() 5 { 6 int i; 7 char ans[10]; 8 scanf("%s",ans); 9 for( i=0; i<10; i++){ 10 printf("%c ",ans[i]); 11 } 12 return 0; 13 }
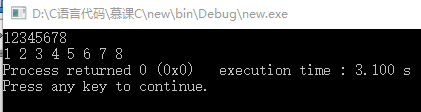
从这里就可以看出,char读入的数组里,高位是放在前面,低位放在后面的。这样放有一个非常不好的就是不方便解决两个长度不一致的数相加的问题。因而在将char型数组转变为int型数组时,习惯将它进行逆置,让低位放在前面,高位放在后面。输出时应该从后往前输出。
下面这道题是加法计算,思路就是将对应两个数组位置的数与前一位的进位相加
题目描述
实现一个加法器,使其能够输出a+b的值。
输入描述:
输入包括两个数a和b,其中a和b的位数不超过1000位。
输出描述:
可能有多组测试数据,对于每组数据, 输出a+b的值。
示例1
输入
2 6 10000000000000000000 10000000000000000000000000000000
输出
8 10000000000010000000000000000000
1 #include<stdio.h> 2 #include<stdlib.h> 3 #include<string.h> 4 5 char a[1001]; 6 char b[1001]; 7 int ansa[1001]; //转换后的a 8 int ansb[1001]; //转换后的b 9 int ans[1002]; //输出目标 10 11 int main() 12 { 13 int i; 14 int lena,lenb; 15 int temp,fd; 16 while( scanf("%s%s",a,b)!=EOF) 17 { 18 lena = strlen(a); 19 lenb = strlen(b); 20 memset(ansa,0,1001*sizeof(int)); 21 memset(ansb,0,1001*sizeof(int)); 22 memset(ans,0,1002*sizeof(int)); 23 fd = 0; //进位 24 for( i=0; i<lena; i++) 25 ansa[i] = a[lena-1-i]-'0'; //注意这里是从后往前 26 for( i=0; i<lenb; i++) 27 ansb[i] = b[lenb-1-i]-'0'; 28 29 if( lena<lenb ) lena = lenb; //选择两个中较大数 30 31 for( i=0; i<lena; i++) 32 { 33 temp = ansa[i]+ansb[i]+fd; 34 fd = temp/10; 35 ans[i] = temp%10; 36 } 37 if( fd ) printf("%d",fd); //如果最后一次进位不为0则先输出 38 for( i=lena-1; i>=0; i--) printf("%d",ans[i]); 39 printf(" "); 40 } 41 return 0; 42 }
下面这道题是高精度的乘法,这个问题主要就是一个大数乘一个小数(两个大数相乘数字就很大了)
用小乘数乘大乘数的每一位数并加上来自低位的进位,从而得到该位的结果以及向高位的进位。
题目描述
输入一个正整数N,输出N的阶乘。
输入描述:
正整数N(0<=N<=1000)
输出描述:
输入可能包括多组数据,对于每一组输入数据,输出N的阶乘
示例1
输入
4 5 15
输出
24 120 1307674368000
1 #include<stdio.h> 2 #include<stdlib.h> 3 #include<string.h> 4 5 int ans[10000]; //输出目标 6 7 int main() 8 { 9 int n; 10 int i,j; 11 int temp,fd; 12 int index; 13 while( scanf("%d",&n)!=EOF) 14 { 15 memset(ans,0,10000*sizeof(int)); 16 index=0; //数组下标,统计个数 17 ans[index++] = 1; //阶乘第一位为1 18 19 for( i=2; i<=n; i++) 20 { 21 fd=0; //进位置0 22 for( j=0; j<index; j++) 23 { 24 temp = ans[j]*i+fd; 25 ans[j] = temp%10; 26 fd = temp/10; 27 } 28 while( fd ) 29 { 30 //这里要小心最高位进位可能有多位 31 ans[index++] = fd%10; 32 fd /= 10; 33 } 34 } 35 for( i=index-1; i>=0; i--) 36 { 37 printf("%d",ans[i]); 38 } 39 } 40 41 return 0; 42 }
最后一个是有关高精度求余问题,这个主要用于进制转换了
题目描述
将一个长度最多为30位数字的十进制非负整数转换为二进制数输出。
输入描述:
多组数据,每行为一个长度不超过30位的十进制非负整数。 (注意是10进制数字的个数可能有30个,而非30bits的整数)
输出描述:
每行输出对应的二进制数。
示例1
输入
0 1 3 8
输出
0 1 11 1000
1 #include<stdio.h> 2 #include<stdlib.h> 3 #include<string.h> 4 5 int main() 6 { 7 char a[50]; 8 int data[50]; //存放转换后的数字 9 int ans[150]; //存放目标二进制数 10 int len; 11 int i,j; 12 int fd,temp,index; 13 while( scanf("%s",a)!=EOF) 14 { 15 len = strlen(a); 16 index = 0; //数组下标初始化为0 17 for( i=0; i<len; i++) 18 { 19 data[len-1-i] = a[i] - '0'; 20 } 21 22 for( i=len-1; i>=0; ) 23 { 24 fd = 0 ; //余数初始化为0 25 for( j=i; j>=0; j--) 26 { 27 temp = data[j]+ fd*10; //fd*10是因为fd是高位对2的余数 28 fd = temp % 2; 29 data[j] = temp / 2; 30 } 31 ans[index++] = fd; 32 if( data[i]==0 ) i--; //只有在该位求余到0才从下一位开始 33 } 34 35 for( i=index-1; i>=0; i--) 36 printf("%d",ans[i]); 37 38 } 39 return 0; 40 }