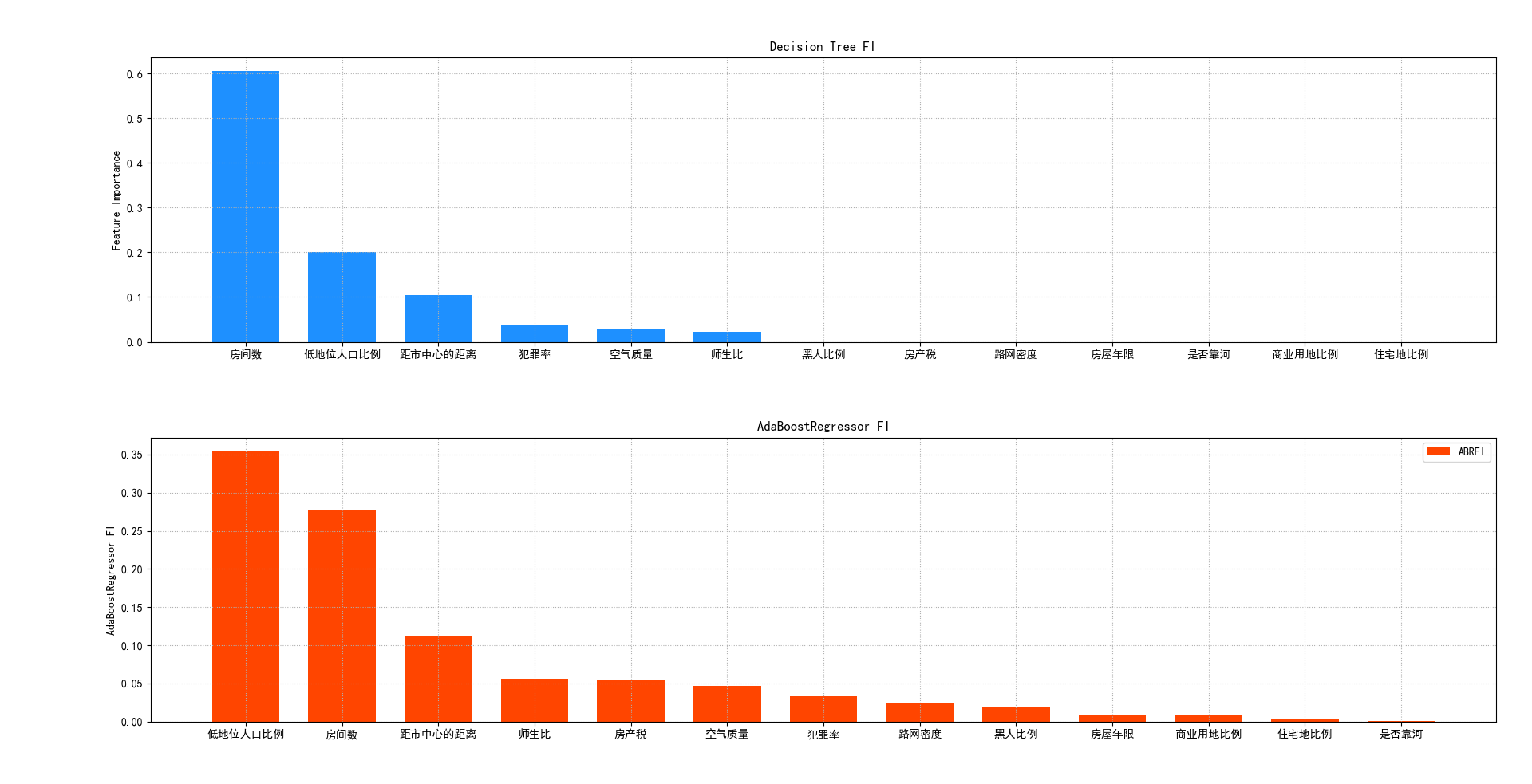
''' 决策树: 基本算法原理: 核心思想:相似的输入必会产生相似的输出。例如预测某人薪资: 年龄:1-青年,2-中年,3-老年 学历:1-本科,2-硕士,3-博士 经历:1-出道,2-一般,3-老手,4-骨灰 性别:1-男性,2-女性 | 年龄 | 学历 | 经历 | 性别 | ==> | 薪资 | | ---- | ---- | ---- | ---- | ---- | -----------| | 1 | 1 | 1 | 1 | ==> | 6000(低) | | 2 | 1 | 3 | 1 | ==> | 10000(中) | | 3 | 3 | 4 | 1 | ==> | 50000(高) | | ... | ... | ... | ... | ==> | ... | | 1 | 3 | 2 | 2 | ==> | ? | 为了提高搜索效率,使用树形数据结构处理样本数据:先按照年龄分三棵子树,再按照学历往下分,知直到所有特征都分完 这样便得到叶级子表,叶级子表中便保存了所有特征值完全相同的样本。 首先从训练样本矩阵中选择第一个特征进行子表划分,使每个子表中该特征的值全部相同, 然后再在每个子表中选择下一个特征按照同样的规则继续划分更小的子表,不断重复直到所有的特征全部使用完为止, 此时便得到叶级子表,其中所有样本的特征值全部相同。对于待预测样本,根据其每一个特征的值,选择对应的子表, 逐一匹配,直到找到与之完全匹配的叶级子表,用该子表中样本的输出,通过平均(回归)或者投票(分类)为待预测样本提供输出。 随着子表的划分,信息熵(信息的混乱程度)越来越小,信息越来越纯,数据越来越有序。 决策树回归器模型相关API: import sklearn.tree as st # 创建决策树回归器模型 决策树的最大深度为4 model = st.DecisionTreeRegressor(max_depth=4) # 训练模型 # train_x: 二维数组样本数据 # train_y: 训练集中对应每行样本的结果 model.fit(train_x, train_y) # 测试模型 pred_test_y = model.predict(test_x) 决策树模型优化: 1.工程优化:不必用尽所有的特征,叶级子表中允许混杂不同的特征值,以此降低决策树的层数,在精度牺牲可接受的前提下, 提高模型的性能。通常情况下,可以优先选择使信息熵减少量最大的特征作为划分子表的依据。 2.集合算法:根据多个不同模型给出的预测结果,利用平均(回归)或者投票(分类)的方法,得出最终预测结果。基于决策树的集合算法, 就是按照某种规则,构建多棵彼此不同的决策树模型,分别给出针对未知样本的预测结果, 最后通过平均或投票得到相对综合的结论。---一棵树片面,多棵树综合起来,泛化模型 1>正向激励:首先为样本矩阵中的样本随机分配初始权重,由此构建一棵带有权重的决策树, 在由该决策树提供预测输出时,通过加权平均或者加权投票的方式产生预测值。 将训练样本代入模型,预测其输出,对那些预测值与实际值不同的样本,提高其权重, 由此形成第二棵决策树。重复以上过程,构建出不同权重的若干棵决策树。---一棵树片面,多棵树综合起来,泛化模型 正向激励相关API: import sklearn.tree as st import sklearn.ensemble as se # 集合算法模块 # model: 决策树模型(一颗),即单棵决策树模型 model = st.DecisionTreeRegressor(max_depth=4) # 自适应增强决策树回归模型 # n_estimators:构建400棵不同权重的决策树(需要多少棵树),训练模型 model = se.AdaBoostRegressor(model, n_estimators=400, random_state=7) # 训练模型 model.fit(train_x, train_y) # 测试模型 pred_test_y = model.predict(test_x) 特征重要性:作为决策树模型训练过程的副产品,根据每个特征划分子表前后的信息熵减少量就标志了该特征的重要程度, 此即为该特征重要性指标。训练得到的模型对象提供了属性:feature_importances_来存储每个特征的重要性。 获取样本矩阵特征重要性属性: model.fit(train_x, train_y) fi = model.feature_importances_ # 末尾带有下划线表示,这些属性都是训练之后得到的副产品 案例:基于普通决策树与正向激励决策树预测波士顿地区房屋价格。并获取获取两个模型的特征重要性值,按照从大到小顺序输出绘图。 ''' import numpy as np import matplotlib.pyplot as mp import sklearn.tree as st import sklearn.datasets as sd # sklearn提供的数据集 import sklearn.utils as su # 可以把数据集按照行进行打乱 import sklearn.metrics as sm import sklearn.ensemble as se # 加载波士顿房屋地区房屋价格 boston = sd.load_boston() # ['CRIM','ZN','INDUS','CHAS','NOX','RM','AGE','DIS','RAD','TAX','PTRATIO','B','LSTAT'] # ['犯罪率','住宅地比例','商业用地比例','是否靠河','空气质量','房间数','房屋年限','距市中心的距离','路网密度','房产税','师生比','黑人比例','低地位人口比例'] print(boston.feature_names) # 特征名 print(boston.data.shape) # 数据的输入 print(boston.target.shape) # 数据的输出 # 划分测试集与训练集---二八分,80%用于训练,20%用于测试 # random_state称为随机种子,若打乱时使用的随机种子相同,则得到的结果相同 x, y = su.shuffle(boston.data, boston.target, random_state=7) # 按行打乱数据集 train_size = int(len(x) * 0.8) train_x, test_x, train_y, test_y = x[:train_size], x[train_size:], y[:train_size], y[train_size:] print(train_x.shape) print(test_x.shape) # 基于普通决策树建模-->训练模型-->测试模型-----单棵决策树 model = st.DecisionTreeRegressor(max_depth=4) model.fit(train_x, train_y) pred_test_y = model.predict(test_x) # 获取普通决策树的特征重要性指标 dt_fi = model.feature_importances_ print(dt_fi) # 模型评估---单棵决策树 print(sm.r2_score(test_y, pred_test_y)) print('=======================') # 基于正向激励预测房屋价格 model = se.AdaBoostRegressor(model, n_estimators=400, random_state=7) model.fit(train_x, train_y) pred_test_y = model.predict(test_x) # 获取正向激励决策树的特征重要性指标 ad_fi = model.feature_importances_ print(ad_fi) # 正向激励的模型评分 print(sm.r2_score(test_y, pred_test_y)) # 绘制特征重要性图像---特征重要性从高到底排序 mp.figure('Feature Importance', facecolor='lightgray') mp.rcParams['font.sans-serif'] = 'SimHei' mp.subplot(211) mp.title('Decision Tree FI') mp.ylabel('Feature Importance') mp.grid(linestyle=":") # 排序 # names = boston.feature_names names = np.array( ['犯罪率', '住宅地比例', '商业用地比例', '是否靠河', '空气质量', '房间数', '房屋年限', '距市中心的距离', '路网密度', '房产税', '师生比', '黑人比例', '低地位人口比例']) sorted_indexes = dt_fi.argsort()[::-1] # 下标排序,从大到小 x = np.arange(names.size) mp.bar(x, dt_fi[sorted_indexes], 0.7, color='dodgerblue', label='DTFI') mp.xticks(x, names[sorted_indexes]) # 设置x轴坐标 mp.tight_layout() mp.legend() mp.subplot(212) mp.title('AdaBoostRegressor FI') mp.ylabel('AdaBoostRegressor FI') mp.grid(linestyle=":") # 排序 # names = boston.feature_names names = np.array( ['犯罪率', '住宅地比例', '商业用地比例', '是否靠河', '空气质量', '房间数', '房屋年限', '距市中心的距离', '路网密度', '房产税', '师生比', '黑人比例', '低地位人口比例']) sorted_indexes = ad_fi.argsort()[::-1] # 下标排序,从大到小 x = np.arange(names.size) mp.bar(x, ad_fi[sorted_indexes], 0.7, color='orangered', label='ABRFI') mp.xticks(x, names[sorted_indexes]) # 设置x轴坐标 mp.tight_layout() mp.legend() mp.show() 输出结果: ['CRIM' 'ZN' 'INDUS' 'CHAS' 'NOX' 'RM' 'AGE' 'DIS' 'RAD' 'TAX' 'PTRATIO' 'B' 'LSTAT'] (506, 13) (506,) (404, 13) (102, 13) [0.03856422 0. 0. 0. 0.02908806 0.62280298 0. 0.10473383 0. 0. 0.00460542 0. 0.20020548] 0.8202560889408634 ======================= [0.03339581 0.00287794 0.00810414 0.00099482 0.0463733 0.27796803 0.00884059 0.11267449 0.02459319 0.05455562 0.05567394 0.0194009 0.35454723] 0.9068598725149652