作业信息
| 博客班级 | 机器学习实验-计算机18级 |
| 作业要求 | 作业要求 |
| 作业目标 | 理解决策树算法原理,掌握决策树算法框架 |
| 学号 | 3180701301 |
一、实验目的
1.理解决策树算法原理,掌握决策树算法框架;
2.理解决策树学习算法的特征选择、树的生成和树的剪枝;
3.能根据不同的数据类型,选择不同的决策树算法;
4.针对特定应用场景及数据,能应用决策树算法解决实际问题。
二、实验内容
1.设计算法实现熵、经验条件熵、信息增益等方法。
2.实现ID3算法。
3.熟悉sklearn库中的决策树算法;
4.针对iris数据集,应用sklearn的决策树算法进行类别预测。
5.针对iris数据集,利用自编决策树算法进行类别预测。
三、实验报告要求
1.对照实验内容,撰写实验过程、算法及测试结果;
2.代码规范化:命名规则、注释;
3.分析核心算法的复杂度;
4.查阅文献,讨论ID3、5算法的应用场景;
四、实验过程及其步骤
1、
import numpy as np import pandas as pd import matplotlib.pyplot as plt %matplotlib inline from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split from collections import Counter import math from math import log import pprint
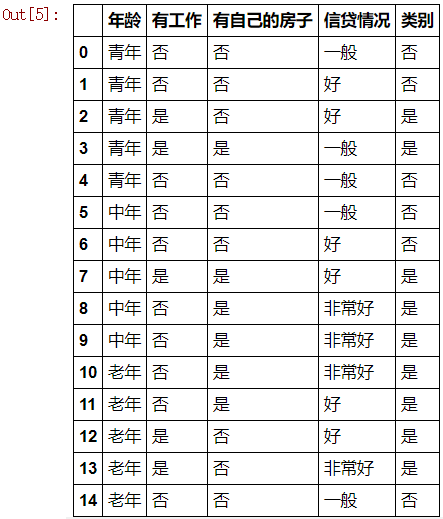
def create_data(): datasets = [['青年', '否', '否', '一般', '否'], ['青年', '否', '否', '好', '否'], ['青年', '是', '否', '好', '是'], ['青年', '是', '是', '一般', '是'], ['青年', '否', '否', '一般', '否'], ['中年', '否', '否', '一般', '否'], ['中年', '否', '否', '好', '否'], ['中年', '是', '是', '好', '是'], ['中年', '否', '是', '非常好', '是'], ['中年', '否', '是', '非常好', '是'], ['老年', '否', '是', '非常好', '是'], ['老年', '否', '是', '好', '是'], ['老年', '是', '否', '好', '是'], ['老年', '是', '否', '非常好', '是'], ['老年', '否', '否', '一般', '否'], ] labels = [u'年龄', u'有工作', u'有自己的房子', u'信贷情况', u'类别'] # 返回数据集和每个维度的名称 return datasets, labels
datasets, labels = create_data()
train_data = pd.DataFrame(datasets, columns=labels)
train_data
X, y = data[:,:-1], data[:,-1] # 数据类型转换,为了后面的数学计算
# 熵 def calc_ent(datasets): data_length = len(datasets) label_count = {} for i in range(data_length): label = datasets[i][-1] if label not in label_count: label_count[label] = 0 label_count[label] += 1 ent = -sum([(p / data_length) * log(p / data_length, 2) for p in label_count.values()]) return ent # def entropy(y): # """ # Entropy of a label sequence # """ # hist = np.bincount(y) # ps = hist / np.sum(hist) # return -np.sum([p * np.log2(p) for p in ps if p > 0]) # 经验条件熵 def cond_ent(datasets, axis=0): data_length = len(datasets) feature_sets = {} for i in range(data_length): feature = datasets[i][axis] if feature not in feature_sets: feature_sets[feature] = [] feature_sets[feature].append(datasets[i]) cond_ent = sum( [(len(p) / data_length) * calc_ent(p) for p in feature_sets.values()]) return cond_ent # 信息增益 def info_gain(ent, cond_ent): return ent - cond_ent def info_gain_train(datasets): count = len(datasets[0]) - 1 ent = calc_ent(datasets) # ent = entropy(datasets) best_feature = [] for c in range(count): c_info_gain = info_gain(ent, cond_ent(datasets, axis=c)) best_feature.append((c, c_info_gain)) print('特征({}) - info_gain - {:.3f}'.format(labels[c], c_info_gain)) # 比较大小 best_ = max(best_feature, key=lambda x: x[-1]) return '特征({})的信息增益最大,选择为根节点特征'.format(labels[best_[0]])
info_gain_train(np.array(datasets))

2、
# 定义节点类 二叉树 class Node: def __init__(self, root=True, label=None, feature_name=None, feature=None): self.root = root self.label = label self.feature_name = feature_name self.feature = feature self.tree = {} self.result = { 'label:': self.label, 'feature': self.feature, 'tree': self.tree } def __repr__(self): return '{}'.format(self.result) def add_node(self, val, node): self.tree[val] = node def predict(self, features): if self.root is True: return self.label return self.tree[features[self.feature]].predict(features) class DTree: def __init__(self, epsilon=0.1): self.epsilon = epsilon self._tree = {} # 熵 @staticmethod def calc_ent(datasets): data_length = len(datasets) label_count = {} for i in range(data_length): label = datasets[i][-1] if label not in label_count: label_count[label] = 0 label_count[label] += 1 ent = -sum([(p / data_length) * log(p / data_length, 2) for p in label_count.values()]) return ent # 经验条件熵 def cond_ent(self, datasets, axis=0): data_length = len(datasets) feature_sets = {} for i in range(data_length): feature = datasets[i][axis] if feature not in feature_sets: feature_sets[feature] = [] feature_sets[feature].append(datasets[i]) cond_ent = sum([(len(p) / data_length) * self.calc_ent(p) for p in feature_sets.values()]) return cond_ent # 信息增益 @staticmethod def info_gain(ent, cond_ent): return ent - cond_ent def info_gain_train(self, datasets): count = len(datasets[0]) - 1 ent = self.calc_ent(datasets) best_feature = [] for c in range(count): c_info_gain = self.info_gain(ent, self.cond_ent(datasets, axis=c)) best_feature.append((c, c_info_gain)) # 比较大小 best_ = max(best_feature, key=lambda x: x[-1]) return best_ def train(self, train_data): """ input:数据集D(DataFrame格式),特征集A,阈值eta output:决策树T """ _, y_train, features = train_data.iloc[:, : -1], train_data.iloc[:, -1], train_data.columns[: -1] # 1,若D中实例属于同一类Ck,则T为单节点树,并将类Ck作为结点的类标记,返回T if len(y_train.value_counts()) == 1: return Node(root=True, label=y_train.iloc[0]) # 2, 若A为空,则T为单节点树,将D中实例树最大的类Ck作为该节点的类标记,返回T if len(features) == 0: return Node( root=True, label=y_train.value_counts().sort_values( ascending=False).index[0]) # 3,计算最大信息增益 同5.1,Ag为信息增益最大的特征 max_feature, max_info_gain = self.info_gain_train(np.array(train_data)) max_feature_name = features[max_feature] # 4,Ag的信息增益小于阈值eta,则置T为单节点树,并将D中是实例数最大的类Ck作为该节点的类标记,返 if max_info_gain < self.epsilon: return Node( root=True, label=y_train.value_counts().sort_values( ascending=False).index[0]) # 5,构建Ag子集 node_tree = Node( root=False, feature_name=max_feature_name, feature=max_feature) feature_list = train_data[max_feature_name].value_counts().index for f in feature_list: sub_train_df = train_data.loc[train_data[max_feature_name] == f].drop([max_feature_name], axis=1) # 6, 递归生成树 sub_tree = self.train(sub_train_df) node_tree.add_node(f, sub_tree) # pprint.pprint(node_tree.tree) return node_tree def fit(self, train_data): self._tree = self.train(train_data) return self._tree def predict(self, X_test): return self._tree.predict(X_test)
datasets, labels = create_data() data_df = pd.DataFrame(datasets, columns=labels) dt = DTree() tree = dt.fit(data_df)
tree

dt.predict(['老年', '否', '否', '一般'])
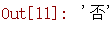
# data def create_data(): iris = load_iris() df = pd.DataFrame(iris.data, columns=iris.feature_names) df['label'] = iris.target df.columns = [ 'sepal length', 'sepal width', 'petal length', 'petal width', 'label' ] data = np.array(df.iloc[:100, [0, 1, -1]]) # print(data) return data[:, :2], data[:, -1] X, y = create_data() X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
from sklearn.tree import DecisionTreeClassifier from sklearn.tree import export_graphviz import graphviz
clf = DecisionTreeClassifier()
clf.fit(X_train, y_train,)

clf.score(X_test, y_test)
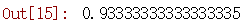
tree_pic = export_graphviz(clf, out_file="mytree.pdf") with open('mytree.pdf') as f: dot_graph = f.read()
graphviz.Source(dot_graph)
from sklearn.tree import DecisionTreeClassifier from sklearn import preprocessing import numpy as np import pandas as pd from sklearn import tree import graphviz features = ["年龄", "有工作", "有自己的房子", "信贷情况"] X_train = pd.DataFrame([ ["青年", "否", "否", "一般"], ["青年", "否", "否", "好"], ["青年", "是", "否", "好"], ["青年", "是", "是", "一般"], ["青年", "否", "否", "一般"], ["中年", "否", "否", "一般"], ["中年", "否", "否", "好"], ["中年", "是", "是", "好"], ["中年", "否", "是", "非常好"], ["中年", "否", "是", "非常好"], ["老年", "否", "是", "非常好"], ["老年", "否", "是", "好"], ["老年", "是", "否", "好"], ["老年", "是", "否", "非常好"], ["老年", "否", "否", "一般"] ]) y_train = pd.DataFrame(["否", "否", "是", "是", "否", "否", "否", "是", "是", "是", "是", "是", "是", "是", "否"]) # 数据预处理 le_x = preprocessing.LabelEncoder() le_x.fit(np.unique(X_train)) X_train = X_train.apply(le_x.transform) le_y = preprocessing.LabelEncoder() le_y.fit(np.unique(y_train)) y_train = y_train.apply(le_y.transform) # 调用sklearn.DT建立训练模型 model_tree = DecisionTreeClassifier() model_tree.fit(X_train, y_train) # 可视化 dot_data = tree.export_graphviz(model_tree, out_file=None, feature_names=features, class_names=[str(k) for k in np.unique(y_train)], filled=True, rounded=True, special_characters=True) graph = graphviz.Source(dot_data) graph
import numpy as np class LeastSqRTree: def __init__(self, train_X, y, epsilon): # 训练集特征值 self.x = train_X # 类别 self.y = y # 特征总数 self.feature_count = train_X.shape[1] # 损失阈值 self.epsilon = epsilon # 回归树 self.tree = None def _fit(self, x, y, feature_count, epsilon): # 选择最优切分点变量j与切分点s (j, s, minval, c1, c2) = self._divide(x, y, feature_count) # 初始化树 tree = {"feature": j, "value": x[s, j], "left": None, "right": None} if minval < self.epsilon or len(y[np.where(x[:, j] <= x[s, j])]) <= 1: tree["left"] = c1 else: tree["left"] = self._fit(x[np.where(x[:, j] <= x[s, j])], y[np.where(x[:, j] <= x[s, j])], self.feature_count, self.epsilon) if minval < self.epsilon or len(y[np.where(x[:, j] > s)]) <= 1: tree["right"] = c2 else: tree["right"] = self._fit(x[np.where(x[:, j] > x[s, j])], y[np.where(x[:, j] > x[s, j])], self.feature_count, self.epsilon) return tree def fit(self): self.tree = self._fit(self.x, self.y, self.feature_count, self.epsilon) @staticmethod def _divide(x, y, feature_count): # 初始化损失误差 cost = np.zeros((feature_count, len(x))) # 公式5.21 for i in range(feature_count): for k in range(len(x)): # k行i列的特征值 value = x[k, i] y1 = y[np.where(x[:, i] <= value)] c1 = np.mean(y1) y2 = y[np.where(x[:, i] > value)] c2 = np.mean(y2) y1[:] = y1[:] - c1 y2[:] = y2[:] - c2 cost[i, k] = np.sum(y1 * y1) + np.sum(y2 * y2) # 选取最优损失误差点 cost_index = np.where(cost == np.min(cost)) # 选取第几个特征值 j = cost_index[0][0] # 选取特征值的切分点 s = cost_index[1][0] # 求两个区域的均值c1,c2 c1 = np.mean(y[np.where(x[:, j] <= x[s, j])]) c2 = np.mean(y[np.where(x[:, j] > x[s, j])]) return j, s, cost[cost_index], c1, c2
train_X = np.array([[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]]).T y = np.array([4.50, 4.75, 4.91, 5.34, 5.80, 7.05, 7.90, 8.23, 8.70, 9.00]) model_tree = LeastSqRTree(train_X, y, .2) model_tree.fit() model_tree.tree

五、实验小结
本次实验学习了决策树决策树算法原理,并且实现了简单的掌握决策树算法,以及决策树学习算法的特征选择、树的生成和树的剪枝。
决策树只需要一次构建,反复使用,效率较高,每一次预测的最大计算次数不超过决策树的深度,可以处理不相关特征数据,能够处理多输出的问题,并且对缺失值不敏感;但是对连续性的字段比较难预测,容易出现过拟合,当类别太多时,错误可能就会增加的比较快,而且对于各类别样本数量不一致的数据,在决策树当中,信息增益的结果偏向于那些具有更多数值的特征。