公众号「前端小苑」,阅读 时间复杂度详解全文。
通过学习本文,你可以掌握以下三点内容。
为什么需要时间复杂度
时间复杂度怎么表示
怎样分析一段代码的时间复杂度
相信认真阅读过本文,面对一些常见的算法复杂度分析,一定会游刃有余,轻松搞定。文章中举的例子,也尽量去贴近常见场景,难度递增。
复杂度是用来衡量代码执行效率的指标,直白讲代码的执行效率就是一段代码执行所需要的时间。
那么,有人会问了,代码执行所需要的时间,我执行一下,看看用了多少时间不就可以了?还要时间复杂度干啥?
一、为什么需要时间复杂度
实际开发时,我们希望自己的代码是最优的,但总不能把所有的实现的方式都写出来,再跑一遍代码做比较,这样不太实际,所以需要一个指标可以衡量算法的效率。
而且,直接跑代码看执行时间会有一些局限性:
1.测试结果受当前运行环境影响
同样的代码在不同硬件的机器上进行测试,得到的测试结果明显会不同。有时候同样是a,b两段代码,在x设备上,a执行的速度比b快,但到了y设备上,可能会完全相反的结果。
2.测试结果受测试数据的影响
不同的测试数据可能会带来不同的结果,比如我们采用顺序查找的方法查找数组中的一个元素,如果这个元素刚好在数组的第一位,执行一次代码就能找到,而如果要找的元素位于数组最后,就要遍历完整个数组才能得到结果。
于是乎,我们需要一个不受硬件,宿主环境和数据集影响的指标来衡量算法的执行效率,它就是算法的复杂度分析。
二、时间复杂度怎么表示
我们知道了为什么需要时间复杂度,那要怎么来表示它呢?下面通过一个简单例子,来说明一下 大O时间复杂度表示法。 首先看第一个例子:
1 function factorial(){
2 let i = 0 // 执行了1次
3 let re = 1 // 执行了1次
4 for(;i < n; i++ ){ // 执行了n次
5 re*= n // 执行了n次
6 }
7 return re // 执行了1次
8 }
上面代码是求n的阶乘(n!)的方法,即n×...×3×2×1
我们粗略的计算一下这段代码的执行时间。 首先,为了方便计算,假设执行每行代码的执行时间是相同的。 在这里,假设每行代码执行一次的时间设为t,代码的总执行时间为T(n)。 代码的第2行,第3行执行了一次,需要的时间是t + t = 2t; 代码的第4行,第5行都执行了n次,所以用时(n + n)t = 2n*t; 代码的第7行,只执行了一次,需要时间 t。
所以执行这段代码的总时间是:
1 T(n) = 2t + 2nt + t = (2n + 3)t
我们以n为x轴,T(n)为y轴,绘制出坐标图如下:
n: **代表数据规模, 相当于上面例子中的n
F(n):表示代码执行次数的总和,代码执行次数的总和与数据规模有关,所以用F(n)表示, F(n)对应上面例子中的(2n+3)
T(n): 代表代码的执行时间,对应上面例子中的T(n)
O: 大O用来表示代码执行时间T(n) 与 代码执行次数总和F(n)之间的正比关系。
现在已经知道了大O表示法公式的含义,我们尝试着把上面例子得出的公式改写成大O表示法,结果如下:
1 T(n) = O(2n + 3)
上面已经说过,大O表示法表示代码执行时间随数据规模增长的变化趋势,只是表示趋势,而不是代表实际的代码执行时间, 当公式中的n无穷大时,系数和常数等对趋势造成的影响就会微乎其微,可以忽略,所以,忽略掉系数和常数,最终上面例子简化成如下的大O表示法:
1 T(n) = O(n)
至此,我们已经知道了什么是大O表示法以及如何使用大O表示法来表示时间复杂度,下面我们利用上面的知识,来分析下面代码的时间复杂度。
1 function reverse(arr){
2 let n = arr.length // 执行了1次
3 let i = 0 // 执行了1次
4 for(;i<n-1;i++){ // 执行了n次
5 let j = 0 // 执行了n次
6 for(j=0;j<n-1;j++){ // 执行了n²次
7 var temp=arr[j] // 执行了n²次
8 arr[j]=arr[j+1] // 执行了n²次
9 arr[j+1]=temp // 执行了n²次
10 }
11 }
12 }
这段代码的目的是颠倒数组中元素的顺序 (代码只是为了方便我们讲解用,不需要考虑代码是否最优),按照之前的分析方法分析,依然设每行代码执行时间为t,代码执行的总时间为T(n)。 第2,3行代码只执行了1次,需要时间2t; 第4,5行代码执行了n次,需要时间 2n*t 第6,7,8,9行代码执行了n²次 所以,执行这段代码的总时间:
1 T(n) = (4n² + 2n + 2)t
去除低阶,系数和常数,最终使用大O表示法表示为:
1 T(n) = O(n²)
通过上面两个例子,我们可以总结出用大O表示法表示时间复杂度的一些规律:
不保留系数
只保留最高阶
嵌套代码的复杂度内外代码复杂度的乘积
三、如何快速分析一段代码的时间复杂度
我们上面总结出了大O表示法的特点,只保留最高阶,所以在分析代码的时间复杂度时,我们只需要关心代码执行次数最多的代码,其他的都可以忽略。 还是看我们上面reverse的例子,执行次数最多的是代码的6,7,8,9行,执行了n²次,我们就可以很容易计算出它的复杂度为大O(n²),这个方法同样适用于存在判断条件的代码。下面是一段带条件判断语句的代码:
1 function test(n){
2 let res = 0
3 if(n > 100){
4 const a = 1
5 const b = 100
6 res = (a + b)*100/2
7 }else {
8 let i = 1
9 for(;i<n; i++){
10 res+=i
11 }
12 }
13 return res
14 }
这段代码的含义是,当n > 100时, 直接返回1-100的和,n < 100时,返回1到n的和。 如果按照n的大小分开分析,当n > 100时,代码的执行时间不随 n 的增大而增长,其时间复杂度记为:
1 T(n) = O(1)
当n <= 100时,时间复杂度为:
1 T(n) = O(n)
上面n > 100的情况,是最理想的情况,这种最理想情况下执行代码的复杂度称为最好情况时间复杂度 n < 100时,是最坏的情况,在这种最糟糕的情况下执行代码的时间复杂度称为最坏情况时间复杂度 后面我们会有单独的文章来分析最好情况时间复杂度,最坏时间复杂度,平均情况时间复杂度, 均摊时间复杂度。
除了特别说明,我们所说的时间复杂度都是指的最坏情况时间复杂度,因为只有在最坏的情况下没有问题,我们对代码的衡量才能有保证。所以我们这种情况,我们依然只需要关注执行次数最多的代码,本例子的时间复杂度为O(n)。
为了方便我们确定哪段代码在计算时间复杂度中占主导地位,熟悉常见函数的时间复杂度对比情况十分必要。
四、常见的时间复杂度
最常见的时间复杂度有常数阶O(1),对数阶O(logn),线性阶O(n),线性对数阶O(nlogn),平方阶O(n²) 从下图可以清晰的看出常见时间复杂度的对比:
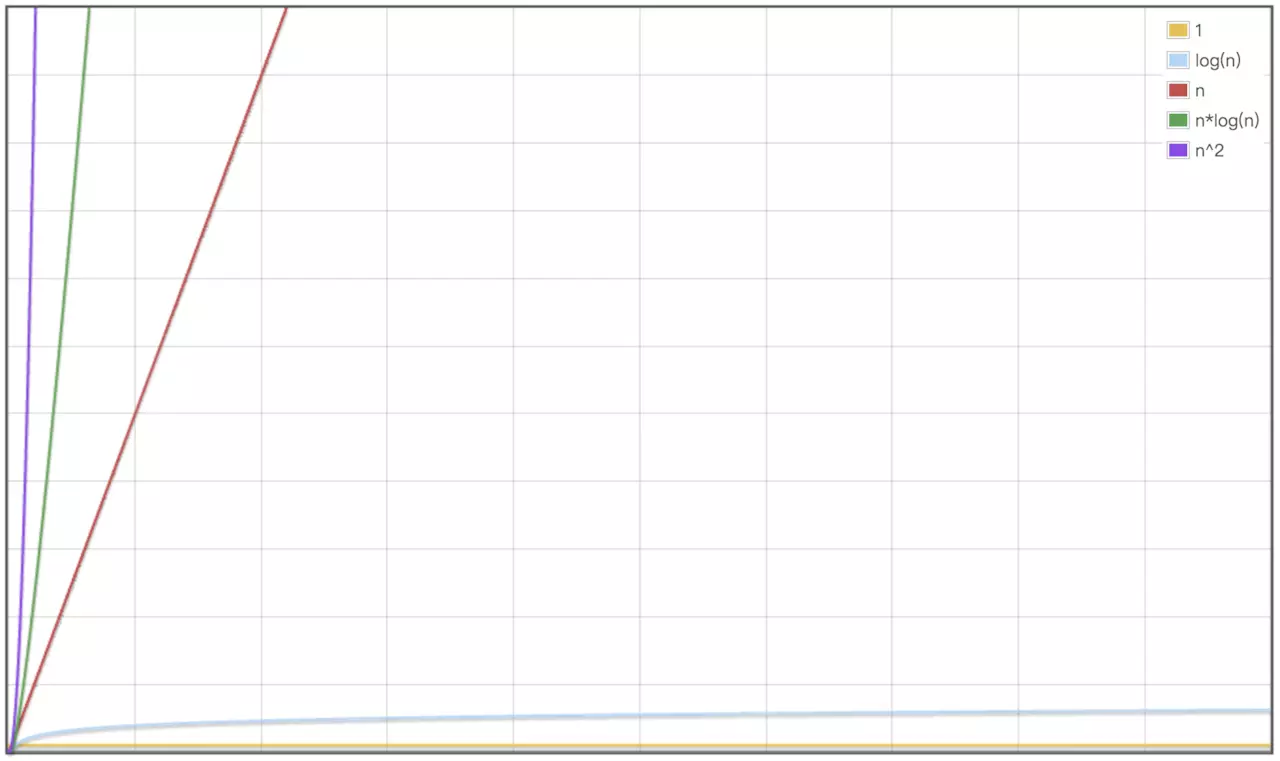
1 O(1) < O(logn) < O(n) < O(nlogn) < O(n^2)
这些常见的复杂度,其中常数阶O(1),线性阶O(n),平方阶O(n²)对我们来说已经不陌生了,在上文的例子中我们已经认识了他们,只有O(logn)还比较陌生,从图中可见对数阶的时间复杂度仅次于常数阶,可以说是性能非常好了。下面就看一个复杂度是对数阶的例子:
1 function binarySearch(arr,key){
2 const n = arr.length
3 let low = 0
4 let high = n - 1
5 let mid = Math.floor((low + high) / 2)
6 while (low <= high) {
7 mid = Math.floor((low + high) / 2)
8 if (key === arr[mid]) {
9 return mid
10 } else if (key < arr[mid]) {
11 high = mid - 1
12 } else {
13 low = mid + 1
14 }
15 }
16 return -1
17 }
这是二分查找查找的代码,二分查找是一个比较高效的查找算法。 现在,我们就分析下二分查找的时间复杂度。 这段代码中执行次数最多的是第7行代码,所以只需要看这段代码的执行次数是多少。上面已经说过,我们现在考虑的都是最坏情况下的时间复杂度,那么对于这段代码,最坏的情况就是一直排除一半,直到只剩下一个元素时才找到结果,或者要找的数组中不存在要找的元素。
现在已知,每次循环都会排除掉1/2不适合的元素,假设执行第T次后,数组只剩余1个元素。
那么:
第1次执行后,剩余元素个数 n/2
第2次执行后,剩余元素个数 n/2/2 = n/4
第3次执行后,剩余元素个数 n/2/2/2 = n/8
... ...
第n次执行后,剩余元素个数 n/(2^T) = 1
由公式 n/(2^T) = 1 可得 2^T = n, 所以总次数等于 log2n,使用大O表示法,省略底数,就是O(logn)
到这里为止,一段简单的代码时间复杂度就可以分析出来了。
更复杂的时间复杂度分析,以及最好情况、最坏情况、平均情况、均摊时间复杂度,将在后面文章中介绍。
如果喜欢本文请扫描下方二维码关注公众号。更多系列原创文章,就在「前端小苑」。