Lecture 7 Training Neural Networks 2
课堂笔记参见:https://zhuanlan.zhihu.com/p/21560667?refer=intelligentunit
本节课主要讲述比较常用的优化算法,正则化方法以及迁移学习。
一、 优化:
随机梯度下降算法是有一些问题的,如图所示,如果目标类似于山坡的最低点,而我们的权重方向W1,W2正好一个竖直,一个水平,对应海森矩阵的最大奇异值和最小奇异值,那么Loss将会对水平更新非常不敏感。这是我们的SGD算法会有什么表现呢?就像如图所示的之字形轨迹一样,一遍遍地越过等高线而不能做到沿着曲面下降。因为SGD算法是沿着超平面上下降最快的方向走的,这个方向可能并没有指向最优点。这张图中下降最快的方向明显是竖直方向,水平方向对Loss的贡献度低导致水平方向基本不移动,这就导致轨迹总是在上下跳动而并没有向最优点显著移动。
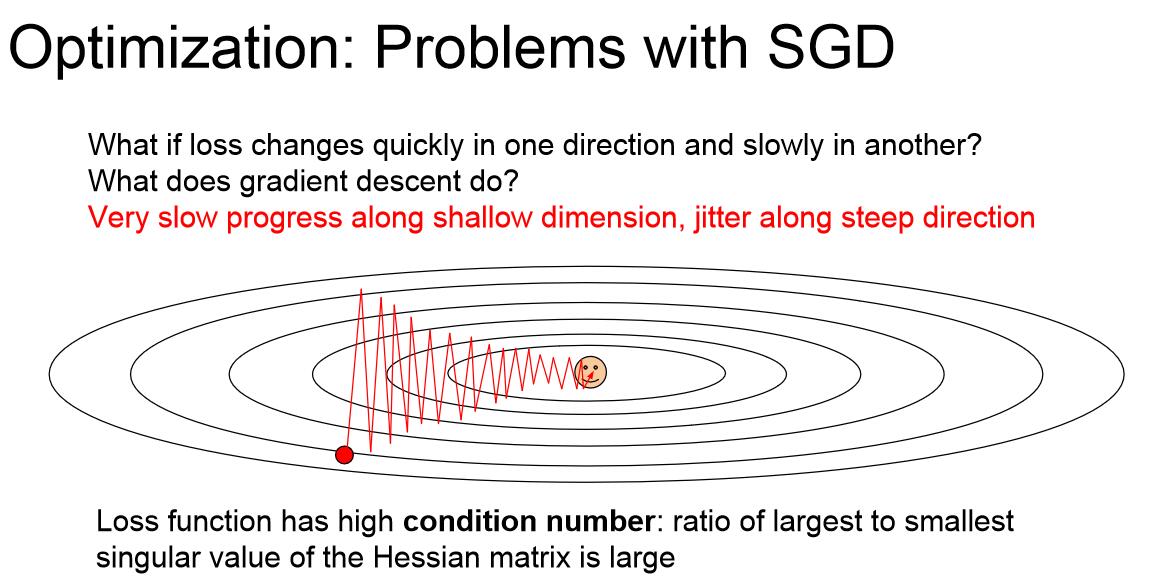
SGD的第二个问题是容易陷入局部极小值。另外对于鞍点(斜率为0)来说,SGD同样会导致函数卡在这一点。在高维问题中,鞍点意味着在当前点上某些方向的损失会增加,某些方向的损失会减小,这种情况在你的参数非常多时是很常见的,而局部极小值意味着在所有方向上行进损失都会增加,在高维网络中这种情况反而并不常见。问题更多地出现在鞍点上。在鞍点附近,梯度值非常小,所以梯度更新会变得异常缓慢。
第三个SGD的问题来源于Stochastic,我们通常不用全部数据来计算Loss,因为每一次迭代都意味着巨大的计算量,我们往往在每一个小batch上计算Loss和梯度作为估计值,这时如果我们在网络中加入随机噪声,我们会发现随机噪声的影响会变得很大,因为梯度下降的随机性可能会使选择出来的数据中噪声成分偏多。在使用所有数据时,这种随机性依然会导致结果受到网络中噪声的影响。
这三个问题都能用一个简单的技巧解决,就是在SGD中加入动量项。

当然这种动量法并不是纯粹物理意义上的动量,而是说梯度更新项会在一定程度上保持原有的趋势(不再是SGD的任意变化),ρ可以理解为是摩擦系数,表示对原梯度值项的衰减因子。这个策略基本解决了我们刚才讨论的所有问题。速度项一般初始化为0。
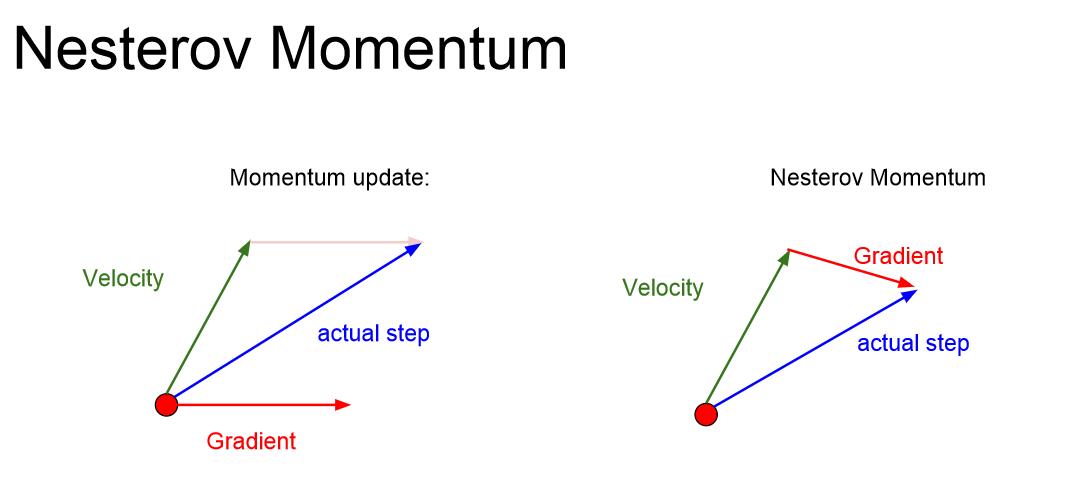
另一种动量方法的思路是Nesterov Momentum:


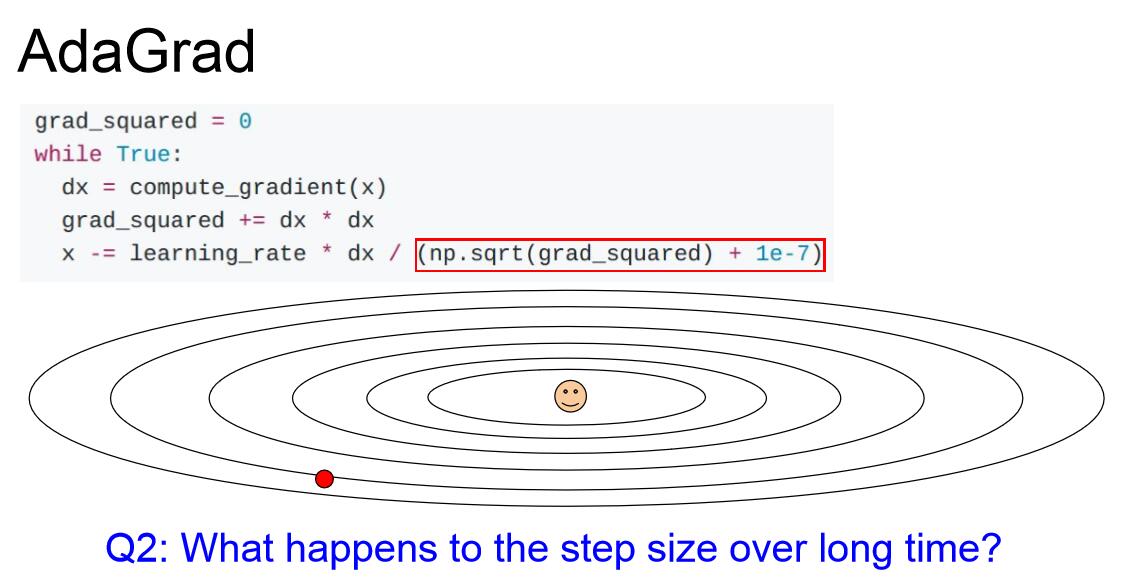
另一种优化思路是斯坦福的John Duchi教授提出的AdaGrad,其核心思想是计算每一步梯度的平方,累加求和,并让参数更新的时候除以这个平方和的平方根。这样如果我们有如上问题二所说的两个W方向,竖直方向得到的大梯度值会使实际的梯度更新较小,而水平方向上的小梯度值会使实际的梯度更新较大,从而解决了问题二。但是随着迭代次数增加,步长会越来越小,这在凸函数逼近中是一个优势,但是非凸函数情形很容易被局部极小值困住。
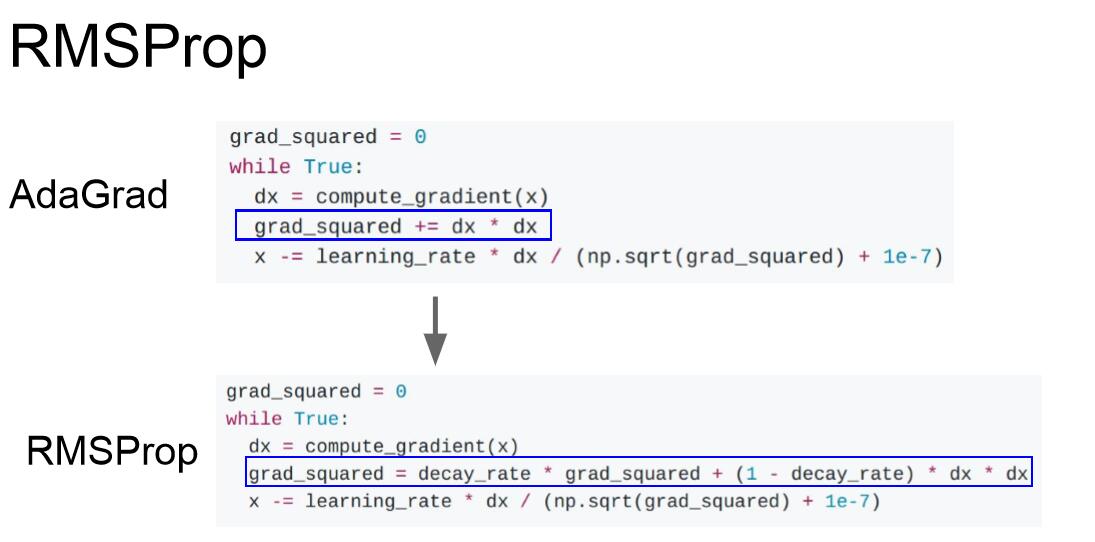
AdaGrad的一个变体是RMSProp,引入了衰减率decay_rate,衰减率通常为0.9或者0.99,用以解决随着迭代次数增加而使步长减小的问题。但是训练速度可能会变慢。
Adam(初期)算法是Momentum 和 RMSProp的结合。相当于在dx,x之间加入了两个变换,dx-first_moment-second_moment-x,分别引入了动量和RMSProp,

然而,如果我们看第一步就会发现,初始值第一、二动量都是零,beta2是0.9或者0.99,所以第一次更新后,第二动量依然很小,这就导致第一步的步长很大。

完善后的Adam引入了偏置校正项,以避免一开始的大步长。Adam几乎对于所有问题表现都很好,所以可以作为我们的默认优化算法。上图中有初始设置值的推荐。
Tips:学习率的设置:
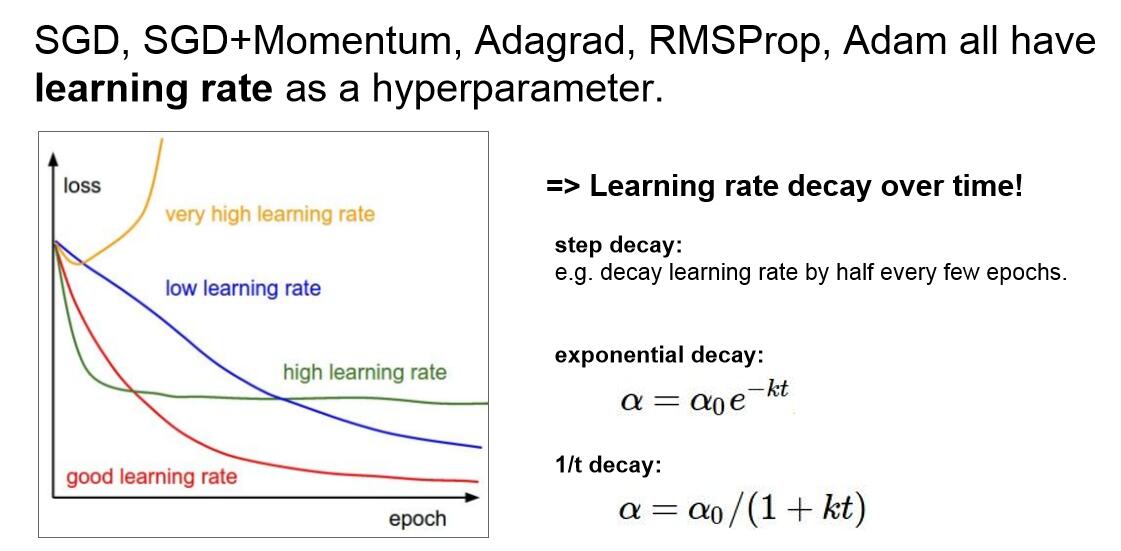
我们之前所讲的都是一阶求导的梯度更新,如果你结合一维变量的二阶求导,然后做一个二阶泰勒逼近,就可以用一个二次函数逼近我们的函数,可以直接跳到函数点的对应最小值点,这就是二阶优化的思想。将问题拓展到多维变量,就是牛顿步长的概念。我们要做的是计算海森矩阵(二阶偏导矩阵),求这个矩阵的逆,以找到二次逼近后的最小值。这个算法就没有学习率的概念了,但是实际运用中我们也会用到学习率,因为这个算法也不是那么完美。
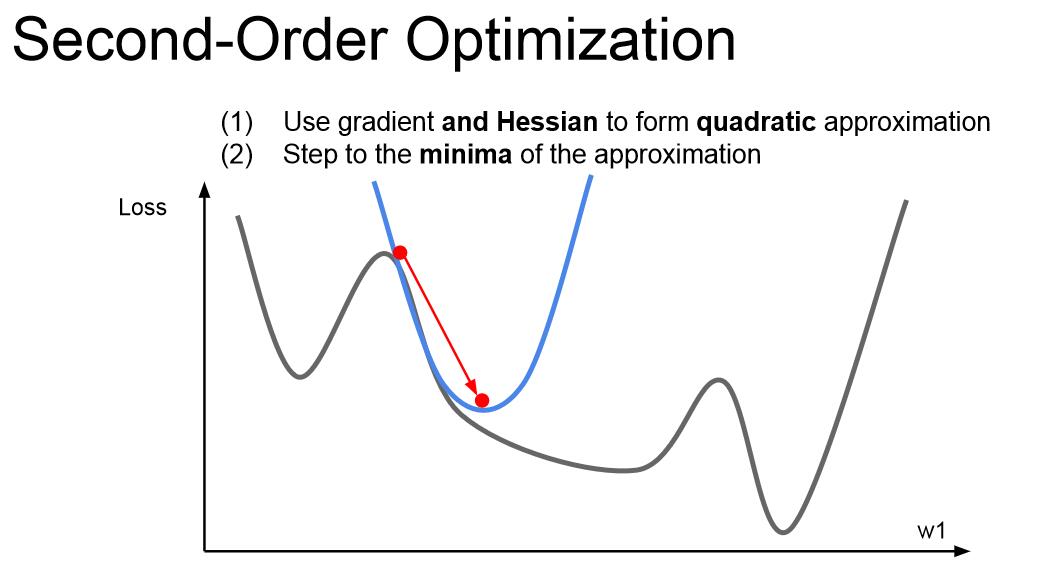
不过,这个算法不适合深度学习,因为海森矩阵是N*N的矩阵(N是网络参数的数量),内存是无法存下这个矩阵的。所以人们经常使用拟牛顿法来替代牛顿法,不直接去求完整的Hessian矩阵的逆,而是去逼近这个矩阵的逆,常用的是低阶逼近。
L-BFGS就是一个二阶优化器,采用了Hessian矩阵的二阶逼近,不过对很多深度学习问题不适用,因为这种逼近算法对随机情况的处理不是那么好,在非凸问题表现也不是很好。当你的网络参数不是很多,随机性也不是很强的时候,L-BFGS有时候会发挥好的效果。
如何减小训练集和验证集Loss的差距呢?一个简单的方法是模型集成(Model Ensembels),相比于训练一个模型,我们选择从不同的随机初始值上训练10个不同的模型,然后在这样的10个模型上运行测试数据,然后平均预测结果,这样可以在一定程度上缓解过拟合,从而提高预测结果。如果发挥一定的想象力,我们并不一定需要真的去训练10个不同的模型,而是在训练过程中获取模型的快照(snapshots),来进行集成学习。在测试阶段,我们将这些快照预测结果做平均。
另外一个trick是我们可以对不同训练时刻的模型参数求指数衰减平均值,从而得到一个比较平滑的集成模型,这叫做Polyak averaging,但事实上并不常用。
二、 正则化:
集成学习时我们需要跑多个模型,那么如何提高单一模型的正确率呢?正则化是可以利用的一个技巧,它在模型中加入一些成分来防止过拟合。

Dropout是另一个正则化中非常常用的技巧。我们把一部分神经元置零,置零指的是将神经元的激活函数置零。一般在全连接层中使用,在卷积层中也会见到,在卷积层中有时候并不是将神经元置零,而是将某些特征映射整体置零,比如讲颜色通道中的某几个整体置零。Dropout一定程度上消除了特征之间的依赖关系,这样网络就只能用一些学习到的零散特征来进行判断。

那么在测试的时候应该怎么做呢?我们原本有输入x,权重w,激活函数f,输出y,但是现在额外有了一个输入z表示被置零的项,z是随机的,这在网络中引入了随机性。你希望在训练的时候可以消除随机性,比如通过如下图所示积分来减小随机性的影响。然而这种积分很难求解,可以通过采样来逼近积分值,比如获取多个z值,在测试的时候把它们平均化,但这样依然会引入一些随机性,并不能达到预期的效果。

我们有一种简单的策略可以逼近这个积分,如果我们考虑单个神经元,输出是a,输入是x,y,以及两个权重w1和w2,用dropout概率p乘以最后的输出,保持预测值和训练值的期望一样,就可以达到简易逼近的效果。

Dropout整体代码只有四行,非常高效:

Tips:有一个很常见的技巧是反转Dropout(inverted dropout),我们希望测试集的代码保持不变,于是在训练集dropout的输出值之后除以p。这样也可以保持训练集输出期望和测试集一致。

相比于dropout这种特殊的实例,更通用的正则化策略是我们在训练的时候给网络添加一些随机性,以防止训练数据的过拟合(随机性在一定程度上扰乱了网络,相当于加入了噪声,使得网络不能完美地关注图片的每一个细节而只是泛化地提取图片特征,这对于防止过拟合十分有效)。测试的时候,我们要抵消掉所有随机性的影响,让测试数据和训练数据保持一致,如图所示。Batch normalization也符合这种思路,所以Batch normalization和dropout的正则化效果类似,在使用Batch normalization的时候,有时候我们不使用dropout的原因就在于此。dropout在实践上更好,因为你可以通过调整p来调整正则化的力度,但是在Batch normalization中没有这种控制机制。

另一种符合这种范式的策略是数据增强(data augmentation),我们可以在训练的时候以某种方式随机地转换图像(比如水平翻转,平移,裁剪,色彩转变,PCA等等),要注意在测试的时候消除这种随机性。Dropconnect同样是一种策略,它并没有将神经元激活函数置零而是将某些权重置零,这样就将全连接变为稀疏连接。Fractional Max Pooling(部分最大池化)也是一个非常cool的想法,一般前向传播中的池化操作是固定的2*2区域,现在我们将随机选择池化区域,如下图所示。在测试的时候有很多方法消除随机性,比如使用一些与训练集池化规模相同的池化区域,或者对一些不同规模的池化区域的样本取平均。
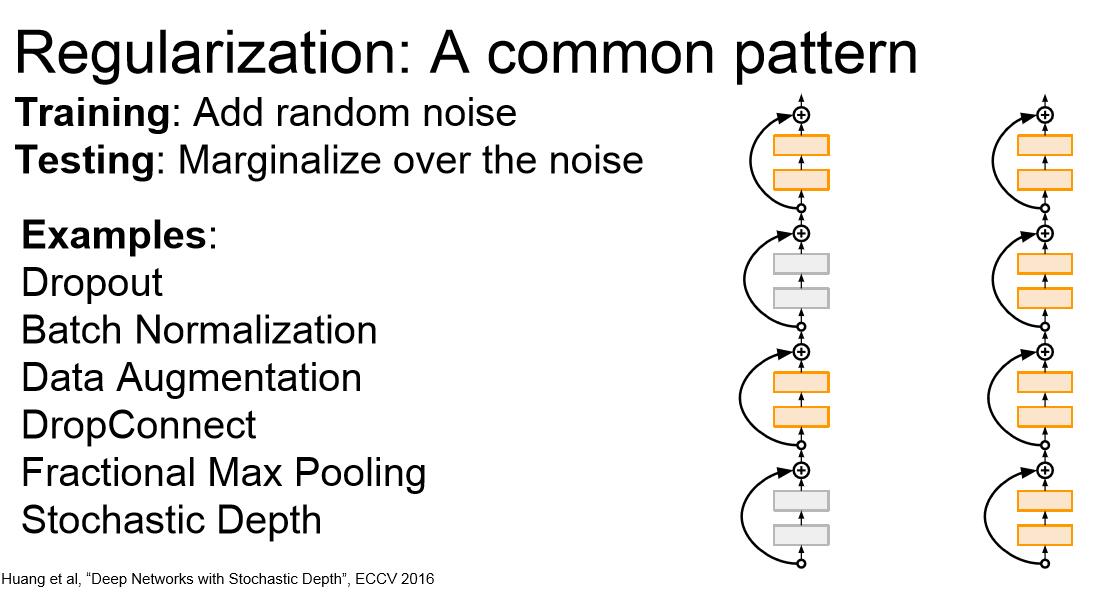
另一个让人眼前一亮的论文是Stochastic Depth(随机深度),对一个深层网络,我们会随机地丢弃网络中的一些层,只用部分层,而在训练时使用全部网络。这种策略的效果近似于dropout。
在日常训练中,我们通常使用Batch normalization,当你发现模型过拟合时,可能会继续增加dropout或者其他的策略。
三、 迁移学习:
transfer learning的思想很简单,就是利用大型数据集上训练好的模型来训练我们更感兴趣的小数据集,只需要改变网络初始化的输入,再在网络最后加入一个线性分类器。进一步你可以微调这个网络,在初步训练之后你可以试着逐渐更新整个网络的权值,这时要注意的是使用小的learning rate,因为网络泛化能力已经很好了,我们要做的只是进行微调以适应我们新的小数据集。

目前在神经网络上的大部分应用,大多数人都不会重新训练,而是在ImageNet上预训练,然后根据具体任务进行精调。如果你没有用一个大数据集的时候,应该做的事下载一些相关的预训练模型,然后要么重新初始化整个模型,要么在你的数据上精调模型。不同软件包里面都提供了这种模型库,你可以下载不同模型的预训练版本。
