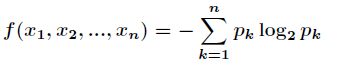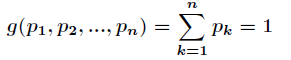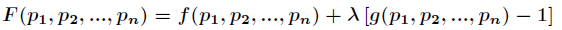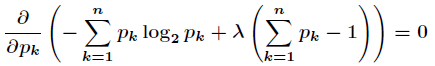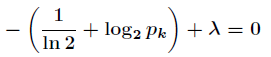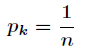https://blog.csdn.net/pipisorry/article/details/52135854
https://blog.csdn.net/yujianmin1990/article/details/48494607
解决约束优化问题——拉格朗日乘数法
拉格朗日乘数法(Lagrange Multiplier Method)应用广泛,可以学习麻省理工学院的在线数学课程。
拉格朗日乘数法的基本思想
作为一种优化算法,拉格朗日乘子法主要用于解决约束优化问题,它的基本思想就是通过引入拉格朗日乘子来将含有n个变量和k个约束条件的约束优化问题转化为含有(n+k)个变量的无约束优化问题。拉格朗日乘子背后的数学意义是其为约束方程梯度线性组合中每个向量的系数。
如何将一个含有n个变量和k个约束条件的约束优化问题转化为含有(n+k)个变量的无约束优化问题?拉格朗日乘数法从数学意义入手,通过引入拉格朗日乘子建立极值条件,对n个变量分别求偏导对应了n个方程,然后加上k个约束条件(对应k个拉格朗日乘子)一起构成包含了(n+k)变量的(n+k)个方程的方程组问题,这样就能根据求方程组的方法对其进行求解。
解决的问题模型为约束优化问题:
min/max a function f(x,y,z), where x,y,z are not independent and g(x,y,z)=0.
即:min/max f(x,y,z)
s.t. g(x,y,z)=0
数学实例
首先,我们先以麻省理工学院数学课程的一个实例来作为介绍拉格朗日乘数法的引子。
【麻省理工学院数学课程实例】求双曲线xy=3上离远点最近的点。
解:
首先,我们根据问题的描述来提炼出问题对应的数学模型,即:
min f(x,y)=x2+y2(两点之间的欧氏距离应该还要进行开方,但是这并不影响最终的结果,所以进行了简化,去掉了平方)
s.t. xy=3.
根据上式我们可以知道这是一个典型的约束优化问题,其实我们在解这个问题时最简单的解法就是通过约束条件将其中的一个变量用另外一个变量进行替换,然后代入优化的函数就可以求出极值。我们在这里为了引出拉格朗日乘数法,所以我们采用拉格朗日乘数法的思想进行求解。
我们将x2+y2=c的曲线族画出来,如下图所示,当曲线族中的圆与xy=3曲线进行相切时,切点到原点的距离最短。也就是说,当f(x,y)=c的等高线和双曲线g(x,y)相切时,我们可以得到上述优化问题的一个极值(注意:如果不进一步计算,在这里我们并不知道是极大值还是极小值)。

现在原问题可以转化为求当f(x,y)和g(x,y)相切时,x,y的值是多少?
如果两个曲线相切,那么它们的切线相同,即法向量是相互平行的,▽f//▽g.
由▽f//▽g可以得到,▽f=λ*▽g。
这时,我们将原有的约束优化问题转化为了一种对偶的无约束的优化问题,如下所示:
原问题:min f(x,y)=x2+y2 对偶问题:由▽f=λ*▽g得,
s.t. xy=3 fx=λ*gx,
fy=λ*gy,
xy=3.
约束优化问题 无约束方程组问题
通过求解右边的方程组我们可以获取原问题的解,即
2x=λ*y
2y=λ*x
xy=3
通过求解上式可得,λ=2或者是-2;当λ=2时,(x,y)=(sqrt(3), sqrt(3))或者(-sqrt(3), -sqrt(3)),而当λ=-2时,无解。所以原问题的解为(x,y)=(sqrt(3), sqrt(3))或者(-sqrt(3), -sqrt(3))。
通过举上述这个简单的例子就是为了体会拉格朗日乘数法的思想,即通过引入拉格朗日乘子(λ)将原来的约束优化问题转化为无约束的方程组问题。
拉格朗日乘数法的基本形态
求函数![]() 在满足
在满足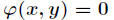 下的条件极值,可以转化为函数
下的条件极值,可以转化为函数 的无条件极值问题。
的无条件极值问题。
我们可以画图来辅助思考。

绿线标出的是约束g(x,y)=c的点的轨迹。蓝线是f(x,y)的等高线。箭头表示斜率,和等高线的法线平行。
从图上可以直观地看到在最优解处,f和g的斜率平行。
▽[f(x,y)+λ(g(x,y)−1)]=0, λ≠0
一旦求出λ的值,将其套入下式,易求在无约束极值和极值所对应的点。
F(x,y)=f(x,y)+λ(g(x,y)−c)
新方程F(x,y)在达到极值时与f(x,y)相等,因为F(x,y)达到极值时g(x,y)−c总等于零。
上述式子取得极小值时其导数为0,即▽f(x)+▽∑λigi(x)=0,也就是说f(x)和g(x)的梯度共线。
题目1:
给定椭球

求这个椭球的内接长方体的最大体积。这个问题实际上就是条件极值问题,即在条件
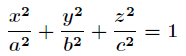
下,求 的最大值。
的最大值。
当然这个问题实际可以先根据条件消去 ,然后带入转化为无条件极值问题来处理。但是有时候这样做很困难,甚至是做不到的,这时候就需要用拉格朗日乘数法了。通过拉格朗日乘数法将问题转化为
,然后带入转化为无条件极值问题来处理。但是有时候这样做很困难,甚至是做不到的,这时候就需要用拉格朗日乘数法了。通过拉格朗日乘数法将问题转化为

对 求偏导得到
求偏导得到

联立前面三个方程得到 和
和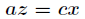 ,带入第四个方程解之
,带入第四个方程解之

带入解得最大体积为

拉格朗日乘数法对一般多元函数在多个附加条件下的条件极值问题也适用。
题目2:
题目:求离散分布的最大熵。
分析:因为离散分布的熵表示如下
而约束条件为
要求函数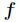
对所有的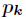
计算出这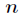
这说明所有的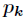
因此,使用均匀分布可得到最大熵的值。
拉格朗日乘数法与KKT条件
拉格朗日乘数法
对于第二种形式,带约束条件的问题,我们更倾向于将其转化为无约束问题。在数学最优化问题中,拉格朗日乘数法是一种寻找变量受一个或多个条件所限制的多元函数的极值的方法。这种方法将一个有n 个变量与k 个约束条件的最优化问题转换为一个有n + k个变量的方程组的极值问题,其变量不受任何约束。这种方法引入了一种新的标量未知数,即拉格朗日乘数(:约束方程的梯度(gradient)的线性组合里每个向量的系数,搞不懂这句话在说神马)。
上面这段话读起来挺绕的,还是举个例子吧。
目标是求f(x,y)=x2∗yf(x,y)=x2∗y的最大值
同时满足x2+y2=1x2+y2=1
怎么将这两个式子凑到一起呢?引入个系数变量λλ
构造新目标函数F(x,y,λ)=x2∗y+λ∗(x2+y2−1)F(x,y,λ)=x2∗y+λ∗(x2+y2−1)
我们看看新目标函数的特点:
对λλ求导,则得:(1)∂f(x,y,λ)∂λ=x2+y2−1∂f(x,y,λ)∂λ=x2+y2−1
对xx求导,则得:(2)∂f(x,y,λ)∂x=2xy+2λx∂f(x,y,λ)∂x=2xy+2λx
对yy求导,则得:(3)∂f(x,y,λ)∂y=x2+2λy∂f(x,y,λ)∂y=x2+2λy
若是按照一个函数的最值存在于其极值的思想来解答,则令这三个式子为0,可以看到,原来的约束也包括进了新目标函数中,不过是引入了个新变量λλ。
并且在F(x,y,λ)F(x,y,λ)取得极值时,与f(x,y)f(x,y)相等,因为FF取得极值时,∂f(x,y,λ)∂λ=x2+y2−1=0∂f(x,y,λ)∂λ=x2+y2−1=0,F(x,y,λ)F(x,y,λ)变为f(x,y)f(x,y)。故,F(x,y,λ)F(x,y,λ)的极值必然是f(x, y)的极值。这段话很重要~
但是这里对原参数的偏导数里多出来的λλ项怎么解释呢?
λλ的物理意义:表示原目标函数在约束下,所能达到的最大增长率(梯度)。其解释如下:
F(w,λ)=f(w)+λ∗g(w)F(w,λ)=f(w)+λ∗g(w);
∂F∂w=∂f∂w+λ∂g∂w∂F∂w=∂f∂w+λ∂g∂w;
∂F∂λ=g(w)∂F∂λ=g(w)
令∂F∂w=0∂F∂w=0,则得λ=−f′wg′wλ=−fw′gw′,可以看出来原目标函数f(w)f(w)的的梯度(最大增长率)受到了g(w)g(w)的梯度约束。
若是将∂F∂λ=g(w)=0∂F∂λ=g(w)=0带入上述λλ式子中,可以得到在确定约束条件下的原目标函数的梯度。(这个说法有问题没有?上面λλ式子已经是在极值下求解得到的,不过没有考虑约束g(x)=0g(x)=0,所以这个说法是没问题的)
(因此,上面的求解最优值,就变成了在约束条件下,原目标函数在约束函数下的梯度求解问题。怎么感觉怪怪的,没想到就变成了这样的问题。错误原因:有地方理解的有问题,对新目标求极值,中间找到了参数间的关系,然后把一个变量表示了出来,只能说明新目标函数在极值时的某个参数的样子)
画个图或许更直观一些。
在约束条件下某目标函数的最值,只可能出现在约束函数的等高线和目标函数在参数面投影的相切的地方。
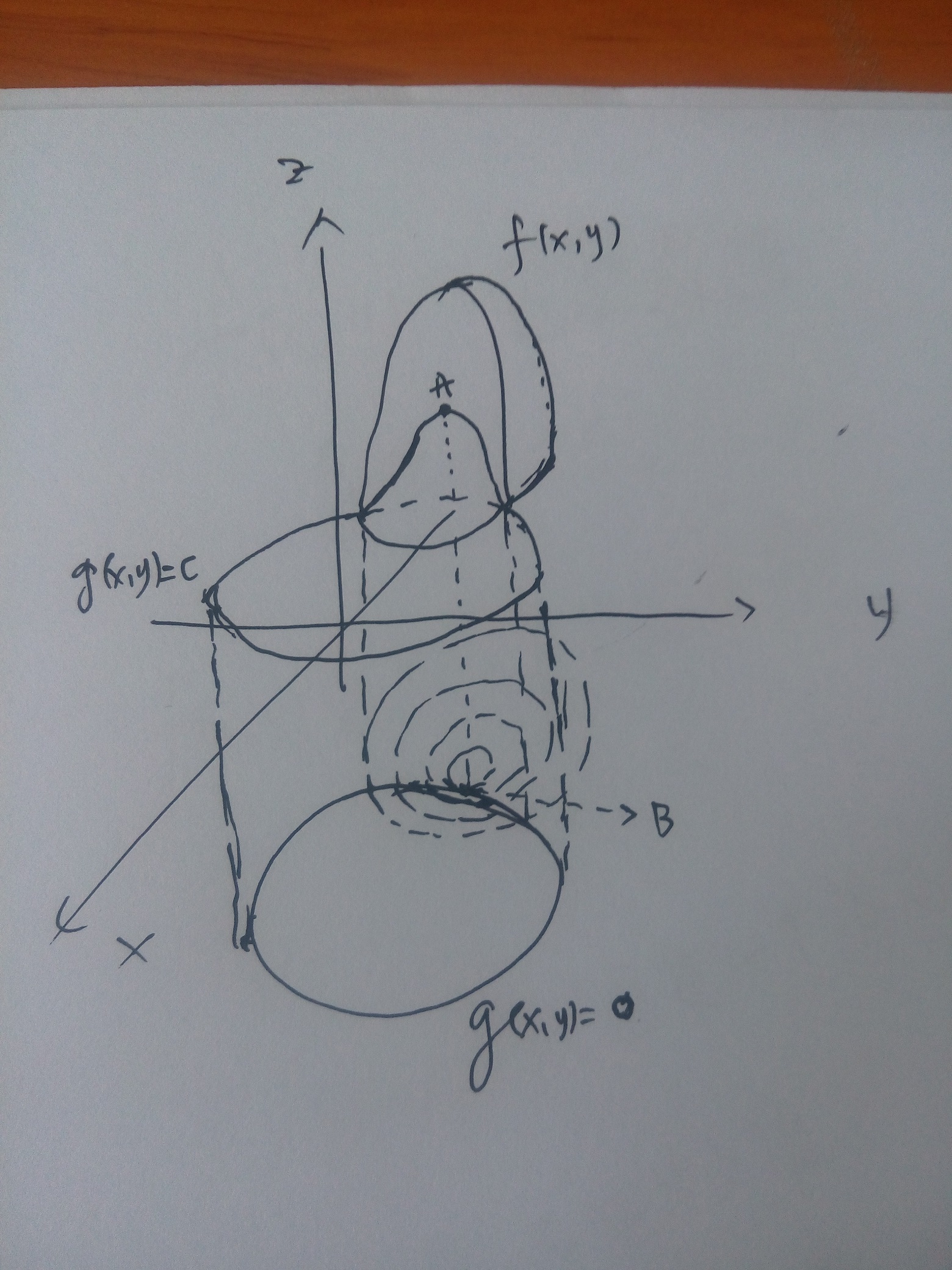
上图中,f(x,y)f(x,y)为目标函数,g(x,y)=cg(x,y)=c为约束条件,我们将两者投影到xyxy平面上得到两者的等高线分布,体现在空间中就是g(x,y)=0g(x,y)=0向上做垂直切面,切割了f(x,y)f(x,y),得到了个曲线,这个曲线投影到xyxy面上刚好与g(x,y)=0g(x,y)=0重合,可以看到随着f(x,y)f(x,y)的xyxy范围缩小(对应其值逐渐增大),会有个与g(x,y)=0g(x,y)=0的切点B,对应于f(x,y)f(x,y)上的A点。A点则是满足约束的,刚好又是最值的地方。
对逻辑回归里惩罚的解释
现在回过头来看,线性回归目标函数里面的惩罚,是怎么个情况,明白了没?结果发现还是没能够解释为什么要加惩罚12wTw12wTw。哎~!~好囧~!~
经过跟马博和贾老师的讨论,终于把这个问题整出了一个较为合理的解释。
首先高次多项式回归的评估函数是误差函数:
cost(x,w)=12∑Mi=1[f(x,w)−y]2cost(x,w)=12∑i=1M[f(x,w)−y]2;前面的1/2是为了后期求导的时候方便。
现在对参数ww进行约束,因为高次对应的参数会很大程度上影响拟合度,并且会有甩尾现象,想把其影响降到较小程度,并且尽可能保留主要部分(w0w0对应的信息)使得泛化能力强,我们想怎么去约束ww呢?
如果wT∗w⩽w20wT∗w⩽w02(二阶范数约束,肯定还有其他约束的情况),那岂不是实现了我们的约束目的,一方面对高次对应的参数进行了约束,一方面他们对整体的影响还不会对整体超过w0w0的影响。
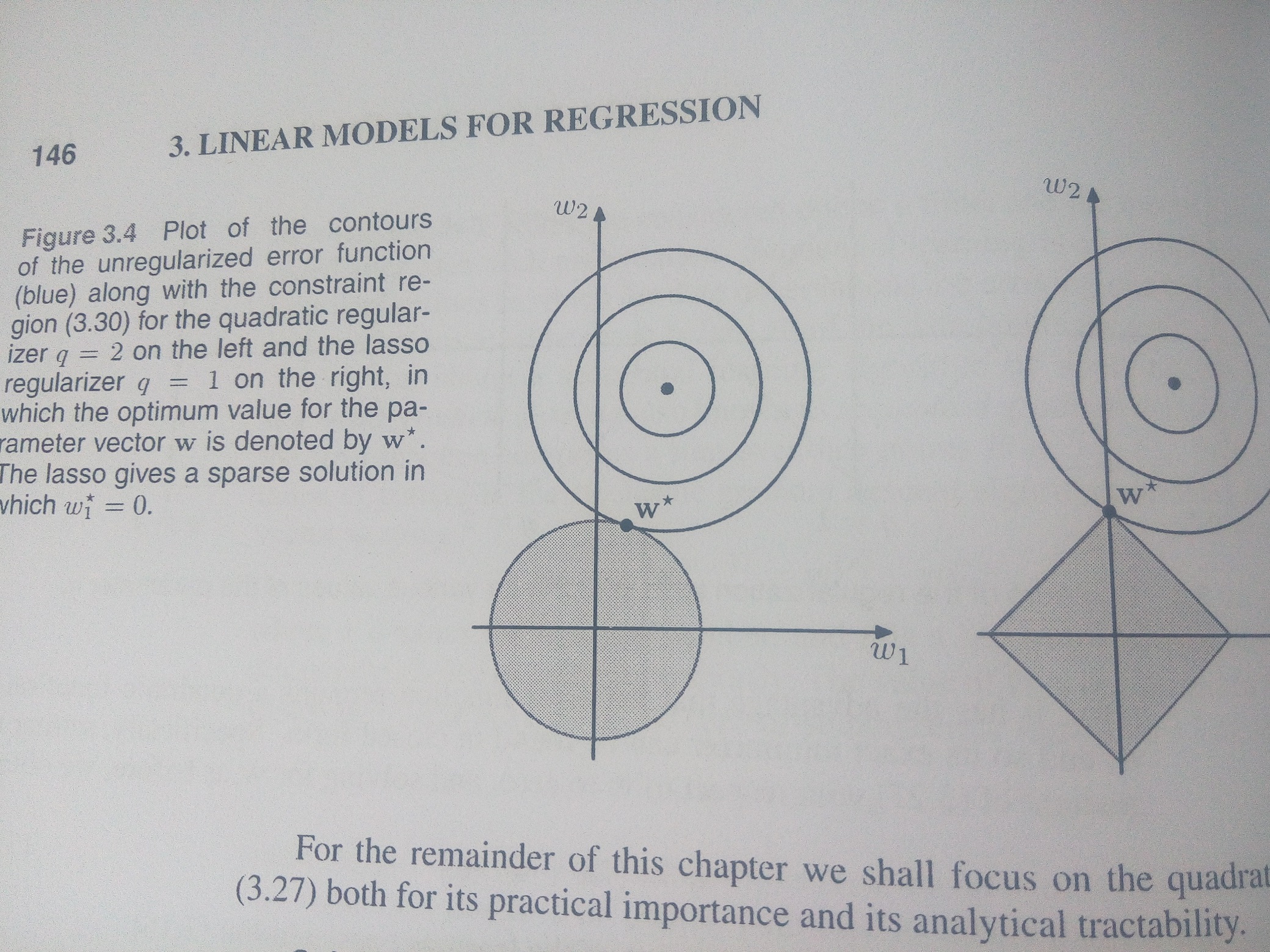
这样,还不能够用拉格朗日乘子法,因为该方法是解决等式约束的最值问题。怎么办呢?好好看看误差函数,这是一个凸函数,我们对ww的约束是在某个范围内,那么根据上面手绘图来看,最值的解只可能出现在,误差函数的等高线与约束最外边缘的切点上。啊哈,这个地方给了我们很大启示,可以直接在约束边缘上找到误差函数的最小值即可。
看下面这个图,就很直观地说明了这个问题。左侧为二阶范数约束,右侧为一阶范数约束。
于是对误差函数的在不等式wTw⩽w20wTw⩽w02的最值问题的解,就是误差函数在等式wTw=w20wTw=w02的最值的解。
哈哈,终于可以正大光明的应用拉格朗日乘子法了,于是就有了我们加入惩罚之后的新的代价函数:
Cost(x,w)=∑Mi=1[f(x,w)−y]2+λ[wT∗w−w20]Cost(x,w)=∑i=1M[f(x,w)−y]2+λ[wT∗w−w02]
这地方离着我们在书本上看到的代价函数还有点区别,就是λλ向量统一变成了1212,目测估计是为了方便求解。
可以有其他的约束,比如∑Mj=0|wj|q⩽η∑j=0M|wj|q⩽η
KKT条件下最优求解
对于第三种情况,又有等式约束,又有不等式约束的,怎么搞呢?上面我们是用拉格朗日乘数法搞定的等式约束的问题,那么对于包括有不等式约束的,可不可以把拉格朗日乘数法扩展一下,充分利用它,解决现在的问题呢?答案是可以,就是满足KKT条件时的最值求解。
KKT条件:在满足一些有规则的条件下,一个非线性规划(Nonlinear Programming)问题能有最优化解的一个必要和充分条件。这是一个广义化拉格朗日乘数的成果,KKT是三个作者的首字母,Karush & Kuhn &Tucker。
求解的问题是:
s.t.gi(w)=0,i=1,2,...,n;s.t.gi(w)=0,i=1,2,...,n;
hj(w)⩽0,j=1,2,...,m;hj(w)⩽0,j=1,2,...,m;
什么条件下,上述问题有最值解呢?
KKT出场了~
先说充分条件:
如果有常数μi⩾0μi⩾0及vjvj满足下述条件:
▽f(w)+∑ni=1μi▽gi(w)+∑mj=1vj▽hj(w)=0▽f(w)+∑i=1nμi▽gi(w)+∑j=1mvj▽hj(w)=0
且μigi(w)=0μigi(w)=0 forfor allall i=1,2,...,ni=1,2,...,n
当然有个重要的前提假设,就是目标函数ff和约束函数gg都是凸函数。
再说必要条件:
如果目标函数和约束函数在某点ww连续可微,点ww为一局部极小值,那么则存在一组所称乘子的常数λ⩾0,λ⩾0, μi⩾0(i=1,2,3,...,n)μi⩾0(i=1,2,3,...,n)及vj(j=1,2,...,m)vj(j=1,2,...,m)满足如下条件:
λ+∑ni=1μi+∑mj=1|vj|>0λ+∑i=1nμi+∑j=1m|vj|>0
λ▽f(w)+∑ni=1μi▽gi(w)+∑mj=1vj▽hj(w)=0λ▽f(w)+∑i=1nμi▽gi(w)+∑j=1mvj▽hj(w)=0
μigi(w)=0μigi(w)=0 forfor i=1,2,...,ni=1,2,...,n
那么这个点ww是全局最小值。(▽▽都是对参数ww求导)
小结
约束下的函数最值问题求解,即将约束问题转化为无约束问题,然后再去解决。
中间会有一些小技巧,自己需要在实际应用中灵活应变。