20192314 2020—2021—1 《数据结构与面向对象程序设计》实验九 图

(1) 初始化：根据屏幕提示（例如：输入1为无向图，输入2为有向图）初始化无向图和有向图（可用邻接矩阵，也可用邻接表），图需要自己定义（顶点个数、边个数，建议先在草稿纸上画出图，然后再输###入顶点和边数）（2分）

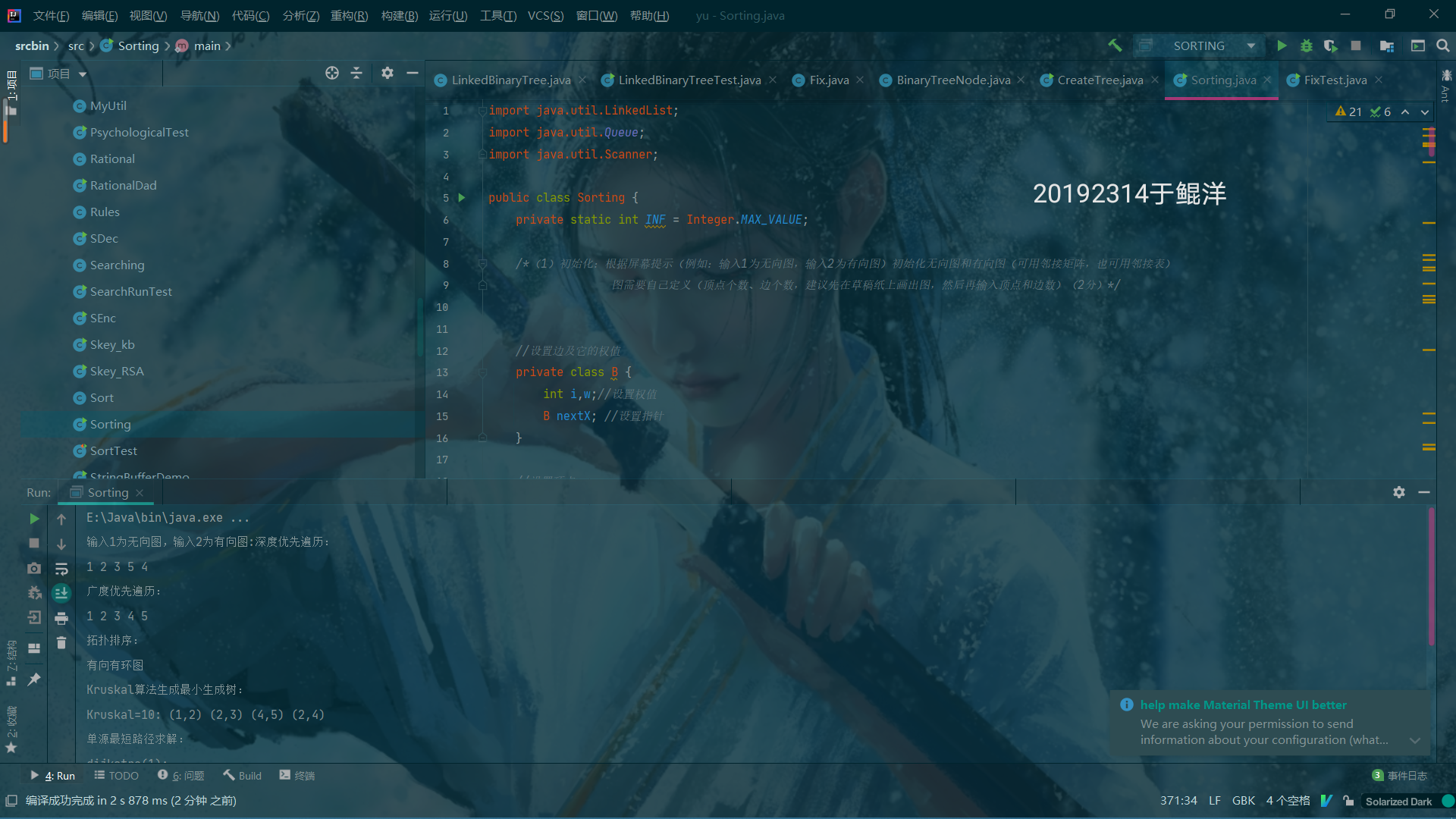
(2) 图的遍历：完成有向图和无向图的遍历（深度和广度优先遍历）（4分）

(3) 完成有向图的拓扑排序，并输出拓扑排序序列或者输出该图存在环（3分）

(4) 完成无向图的最小生成树（Prim算法或Kruscal算法均可），并输出（3分）

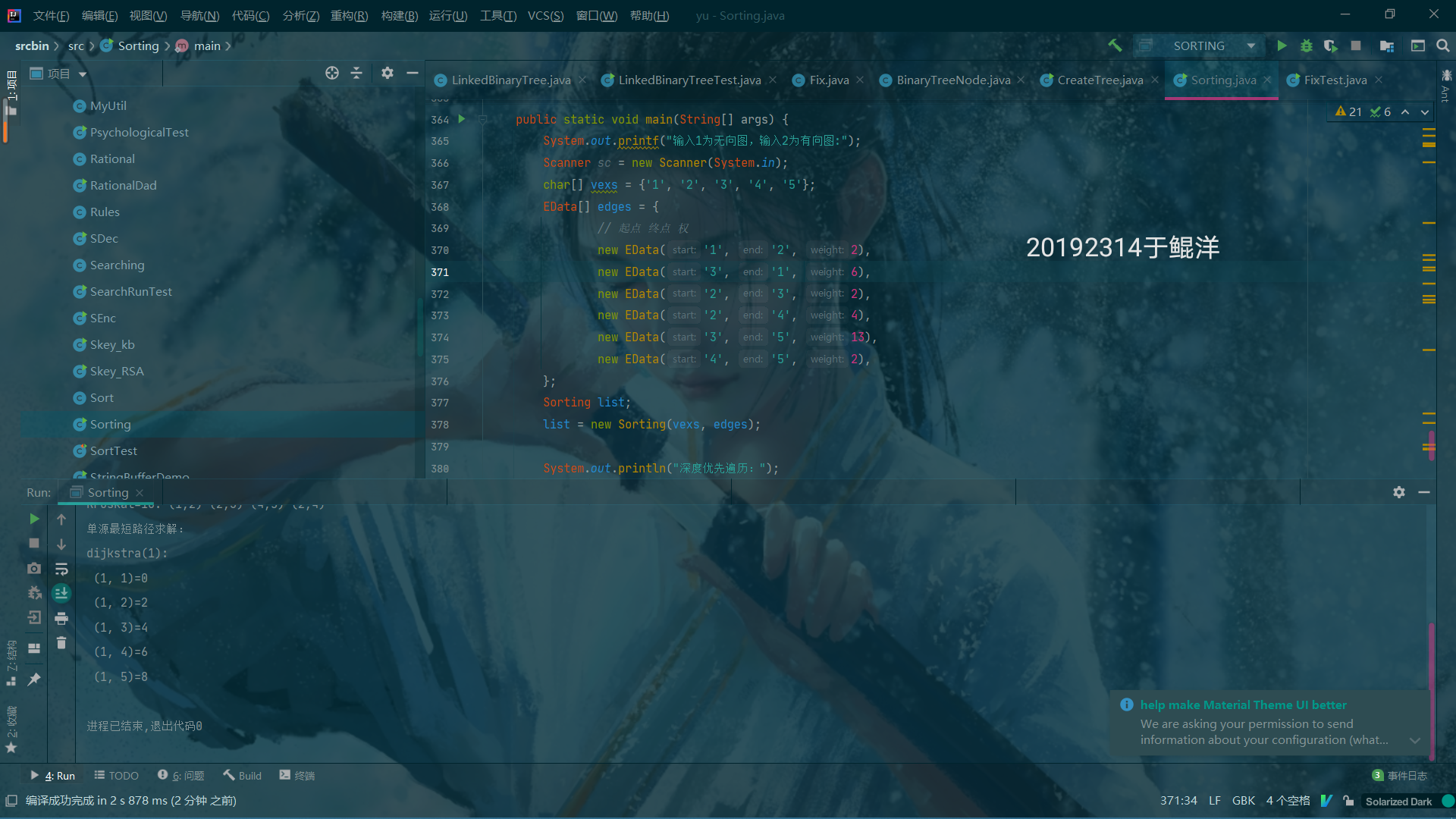
(5) 完成有向图的单源最短路径求解（迪杰斯特拉算法）（3分）

程序代码

import java.util.LinkedList;
import java.util.Queue;
import java.util.Scanner;
public class Sorting {
private static int INF = Integer.MAX_VALUE;

/*（1）初始化：根据屏幕提示（例如：输入1为无向图，输入2为有向图）初始化无向图和有向图（可用邻接矩阵，也可用邻接表）
              图需要自己定义（顶点个数、边个数，建议先在草稿纸上画出图，然后再输入顶点和边数）（2分）*/


//设置边及它的权值
private class B {
    int i,w;//设置权值
    B nextX; //设置指针
}

//设置顶点
private class N {
    char dingdian;          // 设置顶点
    B  firstX;
};

private int Enum;    // 边的数量
private N[] mV;  // 顶点数组

//创建图
public Sorting(char[] dingdian, EData[] bian) {

    int lenv = dingdian.length;
    int elen = bian.length;

    // 初始化顶点
    mV= new N[lenv];
    for (int i = 0; i < mV.length; i++) {
        mV[i] = new N();
        mV[i].dingdian = dingdian[i];
        mV[i].firstX = null;
    }

    // 初始化边
    Enum = elen;
    for (int i = 0; i < elen; i++) {
        // 读取顶点
        char c1 = bian[i].start;
        char c2 = bian[i].end;
        int weight = bian[i].weight;
        int p1 = gPs(c1);
        int p2 = gPs(c2);
        B  node1 = new B ();
        node1.i = p2;
        node1.w = weight;
        //连接
        if(mV[p1].firstX == null)
            mV[p1].firstX = node1;
        else
            Connect(mV[p1].firstX, node1);
        B  node2 = new B ();
        node2.i = p1;
        node2.w = weight;
        //连接
        if(mV[p2].firstX == null)
            mV[p2].firstX = node2;
        else
            Connect(mV[p2].firstX, node2);
    }
}

private void Connect(B  list, B node) {
    B p = list;

    while(p.nextX!=null)
        p = p.nextX;
    p.nextX = node;
}

private int gPs(char ch) {
    for(int i=0; i<mV.length; i++)
        if(mV[i].dingdian==ch)
            return i;
    return -1;
}


/*（2）图的遍历：完成有向图和无向图的遍历（深度和广度优先遍历）（4分）

        深度优先（递归）
 */
private void DFS(int i, boolean[] BL) {
    B node;

    BL[i] = true;
    System.out.printf("%c ", mV[i].dingdian);
    node = mV[i].firstX;
    while (node != null) {
        if (!BL[node.i])
            DFS(node.i, BL);
        node = node.nextX;
    }
}
public void DFS() {
    boolean[] BL = new boolean[mV.length];
    for (int i = 0; i < mV.length; i++)
        BL[i] = false;


    for (int i = 0; i < mV.length; i++) {
        if (!BL[i])
            DFS(i, BL);
    }
    System.out.printf("
");
}

/*
        广度优先
 */
public void BFS() {
    int head = 0;
    int rear = 0;
    int[] queue = new int[mV.length];            // 辅组队列
    boolean[] BL = new boolean[mV.length];  // 顶点访问标记
    for (int i = 0; i < mV.length; i++)
        BL[i] = false;


    for (int i = 0; i < mV.length; i++) {
        if (!BL[i]) {
            BL[i] = true;
            System.out.printf("%c ", mV[i].dingdian);
            queue[rear++] = i;  // 入队列
        }

        while (head != rear) {
            int j = queue[head++];  // 出队列
            B node = mV[j].firstX;
            while (node != null) {
                int k = node.i;
                if (!BL[k])
                {
                    BL[k] = true;
                    System.out.printf("%c ", mV[k].dingdian);
                    queue[rear++] = k;
                }
                node = node.nextX;
            }
        }
    }
    System.out.printf("
");
}

//（3）完成有向图的拓扑排序，并输出拓扑排序序列或者输出该图存在环

public int TpSort() {
    int index = 0;
    int num = mV.length;
    int[] ins;               // 入度数组
    char[] tops;
    Queue<Integer> queue;

    ins   = new int[num];
    tops  = new char[num];
    queue = new LinkedList<Integer>();

    // 统计每个顶点的入度数
    for(int i = 0; i < num; i++) {

        B  node = mV[i].firstX;
        while (node != null) {
            ins[node.i]++;
            node = node.nextX;
        }
    }

    // 将所有入度为0的顶点入队列
    for(int i = 0; i < num; i ++)
        if(ins[i] == 0)
            queue.offer(i);                 // 入队列

    while (!queue.isEmpty()) {              // 队列非空
        int j = queue.poll().intValue();    // 出队列。j是顶点的序号
        tops[index++] = mV[j].dingdian;
        B  node = mV[j].firstX;
        while(node != null) {
            // 入度减1。
            ins[node.i]--;
            // 若入度为0，则入队列
            if( ins[node.i] == 0)
                queue.offer(node.i);    // 入队列

            node = node.nextX;
        }
    }
    if(index != num) {
        System.out.printf("有向有环图
");
        return 1;
    }
    // 打印拓扑排序结果
    System.out.printf("拓扑排序: ");
    for(int i = 0; i < num; i ++)
        System.out.printf("%c ", tops[i]);
    System.out.printf("
");

    return 0;
}


//完成无向图的最小生成树Kruscal算法并输出
//获得权重
private int getWeight(int start, int end) {

    if (start==end)
        return 0;

    B  node = mV[start].firstX;
    while (node!=null) {
        if (end==node.i)
            return node.w;
        node = node.nextX;
    }

    return INF;
}

public void kruskal() {
    int index = 0;
    int[] v = new int[Enum];     // 保存终点。
    EData[] rets = new EData[Enum];  // 暂存结果数组
    EData[] e;                      // 对应的所有边

    e = getEdges();
    // 将边按权排序
    sortEdges(e, Enum);

    for (int i=0; i<Enum; i++) {
        int p1 = gPs(e[i].start);
        int p2 = gPs(e[i].end);

        int m = getEnd(v, p1);
        int n = getEnd(v, p2);
        // 如果m!=n，则没有形成环路
        if (m != n) {
            v[m] = n;
            rets[index++] = e[i];
        }
    }

    // print
    int length = 0;
    for (int i = 0; i < index; i++)
        length += rets[i].weight;
    System.out.printf("Kruskal=%d: ", length);
    for (int i = 0; i < index; i++)
        System.out.printf("(%c,%c) ", rets[i].start, rets[i].end);
    System.out.printf("
");
}


private EData[] getEdges() {
    int index=0;
    EData[] edges;

    edges = new EData[Enum];
    for (int i=0; i < mV.length; i++) {

        B  node = mV[i].firstX;
        while (node != null) {
            if (node.i > i) {
                edges[index++] = new EData(mV[i].dingdian, mV[node.i].dingdian, node.w);
            }
            node = node.nextX;
        }
    }

    return edges;
}

private void sortEdges(EData[] edges, int elen) {

    for (int i=0; i<elen; i++) {
        for (int j=i+1; j<elen; j++) {

            if (edges[i].weight > edges[j].weight) {
                // 交换"边i"和"边j"
                EData tmp = edges[i];
                edges[i] = edges[j];
                edges[j] = tmp;
            }
        }
    }
}

/*
 * 获取i的终点
 */
private int getEnd(int[] vends, int i) {
    while (vends[i] != 0)
        i = vends[i];
    return i;
}


//(5) 完成有向图的单源最短路径求解（迪杰斯特拉算法）
public void dijkstra(int s, int[] q, int[] t) {
    // flag[i]=true表示最短路径已成功获取。
    boolean[] flag = new boolean[mV.length];

    // 初始化
    for (int i = 0; i < mV.length; i++) {
        flag[i] = false;
        q[i] = 0;                // 顶点i的前驱顶点为0。
        t[i] = getWeight(s, i);
    }

    // 初始化
    flag[s] = true;
    t[s] = 0;


    int k = 0;
    for (int i = 1; i < mV.length; i++) {
        // 寻找当前最小的路径；
        // 寻找当前最小的路径；
        // 寻找当前最小的路径；
        int min = INF;
        for (int j = 0; j < mV.length; j++) {
            if (flag[j]==false && t[j]<min) {
                min = t[j];
                k = j;
            }
        }
        // 获取到最短路径
        flag[k] = true;
        for (int j = 0; j < mV.length; j++) {
            int tmp = getWeight(k, j);
            tmp = (tmp==INF ? INF : (min + tmp)); // 防止溢出
            if (flag[j]==false && (tmp<t[j]) )
            {
                t[j] = tmp;
                q[j] = k;
            }
        }
    }

    //print
    System.out.printf("dijkstra(%c): 
", mV[s].dingdian);
    for (int i = 0; i < mV.length; i++)
        System.out.printf(" (%c, %c)=%d
", mV[s].dingdian, mV[i].dingdian, t[i]);
}

// 边的结构体
private static class EData {
    char start; // 边的起点
    char end;   // 边的终点
    int weight; // 边的权重

    public EData(char start, char end, int weight) {
        this.start = start;
        this.end = end;
        this.weight = weight;
    }
};


public static void main(String[] args) {
    System.out.printf("输入1为无向图，输入2为有向图:");
    Scanner sc = new Scanner(System.in);
    char[] vexs = {'1', '2', '3', '4', '5', '6', '7'};
    EData[] edges = {
            // 起点 终点 权
            new EData('1', '2', 2),
            new EData('1', '6', 6),
            new EData('1', '4', 2),
            new EData('2', '5', 13),
            new EData('2', '3',  7),
            new EData('3', '6',  4),
            new EData('3', '5',  5),
            new EData('3', '4',  1),
            new EData('4', '6',  2),
            new EData('5', '6',  2),
            new EData('5', '7',  1),
            new EData('6', '7',  2),
    };
    Sorting list;
    list = new Sorting(vexs, edges);

    System.out.println("深度优先遍历：");
    list.DFS();
    System.out.println("广度优先遍历：");
    list.BFS();
    System.out.println("拓扑排序：");
    list.TpSort();
    System.out.println("Kruskal算法生成最小生成树：");
    list.kruskal();

    int[] q = new int[list.mV.length];
    int[] t = new int[list.mV.length];
    System.out.println("单源最短路径求解：");
    list.dijkstra(0, q, t);

}}

运行截图

实验心得

这次的实验是将之前学过的许多内容进行结合和综合运用，难度并不是很大，但是需要细细思考和耐心理解。不然还有很多地方容易出错，比如有向无向，有环无环。