爬山算法/A Star not a Tree?

爬山算法是用来解决一个不规律函数的最值问题的一个算法，其基本算法是每一次向周围走一步，并比对一下是否更优，如果更优的话就更改目前的位置，如果不是的话就不进行更改。

但是爬山算法的劣势也是比较显然的，由于达到局部最优解之后就很难跳出这个区间最低点，所以很容易陷入局部最优解，盗一张图：

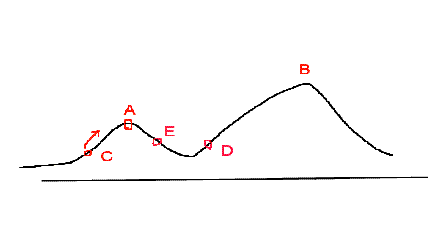
那么爬山算法就一点用也没有吗，不是的，我们为了提高正确性，我们可以随机的取几个点，分别进行该操作，最后取一个最好的结果，那么在很大概率下他是正确的，所以爬山算法的参数选择性是很重要的，而且一般只能解决函数分布比较均匀的题目。

例题：

A Star not a Tree?

题目大意：

给定一个N边形所有顶点坐标x,y，求其费马点到所有顶点距离和

费马点是指到多边形所有顶点距离和最小的点

这道题我们可以用爬山算法解决，考虑到正确率，我们可以随机选择多个点进行测试，我选择了五个，然后对于他们进行比较，取最优的一个。

对于每一个点，我们设定一个初始步数step，一般开的最好大一点，然后我们每一次向上下左右走这个步数，如果遇到更优的点就替换，没有就继续执行原来的点，并且步数要不断减小，当步数小于一定值的时候就停止操作。

尽管我们会陷入局部最优解，但是我们用多个点比对，还是很有可能找到最优解的。

最后，附上本题代码：

#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<algorithm>
#include<ctime>
using namespace std;

struct node
{
    double x,y,d;
} a[110];
int n,T;
const int dtx[4]={0,1,0,-1},dty[4]={1,0,-1,0};
double ans;

inline double pow2(double x)
{
    return x*x;
}
inline double getdis(node u)
{
    double dis=0;
    for(int i=1;i<=n;i++) dis+=sqrt(pow2(u.x-a[i].x)+pow2(u.y-a[i].y));
    return dis;
}
double solve()
{
    node u;
    u.x=rand()%10001,u.y=rand()%10001;
    u.d=getdis(u);
    double step=1e4;
    while(step>1e-3)
    {
        node next,v;
        next.x=u.x+dtx[0]*step;
        next.y=u.y+dty[0]*step;
        next.d=getdis(next);
        for(int i=1;i<=3;i++)
        {
            v.x=u.x+dtx[i]*step;
            v.y=u.y+dty[i]*step;
            v.d=getdis(v);
            if(v.d<next.d) next=v;
        }
        if(next.d<u.d) u=next;
        step*=0.5;
    }
    return u.d;
}
int main()
{
    srand(time(NULL));
    scanf("%d",&T);
    for(int Ti=1;Ti<=T;Ti++)
    {
        scanf("%d",&n);
        for(int i=1; i<=n; i++) scanf("%lf%lf",&a[i].x,&a[i].y);
        ans=1e16;
        for(int i=1;i<=5;i++) ans=min(ans,solve());
        printf("%.0lf
",ans);
        if(T!=Ti) printf("
");
    }
    return 0;
}