Nearest Common Ancestors
题目大意:
求树上两个点的LCA(最近公共祖先)
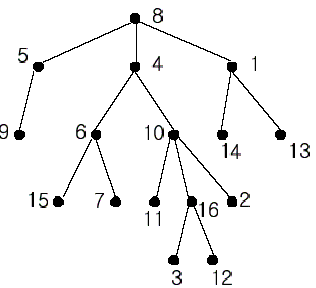
输入格式:
T代表数据组数,n代表节点数目。
n-1行每行两个数a,b分别代表a是b的父节点,ab间有一条无向边。
最后一行为两个数a,b,代表求a,b的LCA。
输出格式:
对于每一组数据输出LCA
思路:裸的LCA了,那么我们就利用最常规的倍增LCA。
首先要找到整个树的根,找根在这道题中比较简单,通过数据输入可知只要不在第二位的节点就是根节点(因为它没有爸爸)
然后我们对于整个树进行预处理,预处理出每一个节点的深度和它向上跳2的i次幂到达的位置,递推公式f[u][i+1]=f[f[u][i]][i](比较显然的)
我们将查询的设为x,y,并且人为规定x的深度大于y,我们首先把x跳到与y深度相同位置,只有跳完后深度大于等于才跳(只要从大到小枚举2的i次幂就行,二进制拆分原理),然后一起往上跳,只有跳完之后到达的点不相同才跳,最后往上走一个即可。
最后附上本题代码:
1 #include<cstdio> 2 #include<iostream> 3 #include<cstring> 4 #define maxn 10000 5 using namespace std; 6 7 struct EDGE 8 { 9 int nxt,to; 10 }; 11 EDGE edge[maxn*2+5]; 12 int T,n,root,cnt; 13 int head[maxn+5],dep[maxn+5]; 14 int f[maxn+5][25]; 15 bool vis[maxn+5]; 16 17 void add(int x,int y) 18 { 19 edge[++cnt].to=y; 20 edge[cnt].nxt=head[x]; 21 head[x]=cnt; 22 } 23 void pre_fir(int u,int fa) 24 { 25 dep[u]=dep[fa]+1; 26 for(int i=0;i<=22;i++) 27 { 28 f[u][i+1]=f[f[u][i]][i]; 29 } 30 for(int i=head[u];i;i=edge[i].nxt) 31 { 32 if(edge[i].to==fa) 33 { 34 continue; 35 } 36 f[edge[i].to][0]=u; 37 pre_fir(edge[i].to,u); 38 } 39 } 40 int LCA(int x,int y) 41 { 42 if(dep[x]<dep[y]) 43 { 44 swap(x,y); 45 } 46 for(int i=22;i>=0;i--) 47 { 48 if(dep[f[x][i]]>=dep[y]) 49 { 50 x=f[x][i]; 51 } 52 if(x==y) 53 { 54 return x; 55 } 56 } 57 for(int i=22;i>=0;i--) 58 { 59 if(f[x][i]!=f[y][i]) 60 { 61 x=f[x][i]; 62 y=f[y][i]; 63 } 64 } 65 return f[x][0]; 66 } 67 int main() 68 { 69 scanf("%d",&T); 70 while(T--) 71 { 72 memset(vis,0,sizeof(vis)); 73 memset(edge,0,sizeof(edge)); 74 memset(f,0,sizeof(f)); 75 memset(dep,0,sizeof(dep)); 76 memset(head,0,sizeof(head)); 77 cnt=0; 78 scanf("%d",&n); 79 for(int i=1;i<=n-1;i++) 80 { 81 int x,y; 82 scanf("%d%d",&x,&y); 83 vis[y]=1; 84 add(x,y); 85 add(y,x); 86 } 87 for(int i=1;i<=n;i++) 88 { 89 if(vis[i]==0) 90 { 91 root=i; 92 break; 93 } 94 } 95 pre_fir(root,0); 96 int a,b; 97 scanf("%d%d",&a,&b); 98 printf("%d ",LCA(a,b)); 99 } 100 return 0; 101 }