一、背景
1975年,Manacher发明了Manacher算法(马拉车算法),是一个可以在(O(n))的复杂度中返回字符串s中最长回文子串长度的算法。
二、算法过程分析
1.输入转化
回文串分为奇回文与偶回文,例如,('ababa')中字符个数为5且为回文串,所以它是奇回文,而'abba'字符个数为4且为回文串,所以它是偶回文。
显然,奇回文与偶回文很是不一样,比较难处理,所以我们将输入的字符串转换一下,规则如下:
1.在第一个字符前添加一个不常用字符(常用'$'),以此充当边界
2.在最后一个字符后添加一个不常用字符(常用'�'),以此充当边界
3.在第一个字符前('$'后),最后一个字符后('�'前)和每两个字符之间添加一个不常用字符(常用'#')
这样以后,上文的'ababa'就会变成'a#b#a#b#a'(边界未标出),'abba'就会变成'a#b#b#a',它们都是奇回文,这样就会更好处理。
2.过程分析
设(F_i)表示以(i)为中点,回文字符串的最大半径长度。
举个例子。令字符串S='abbadcacda'
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (S) | $ | # | a | # | b | # | b | # | a | # | d | # | c | # | a | # | c | # | d | # | a | # | � |
| (F_i) | (phi) | 1 | 2 | 1 | 2 | 5 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 8 | 1 | 2 | 1 | 2 | 1 | 2 | 1 | (phi) |
显然,最终的答案就为(Max_{s_i in S}F_i-1)
那么如何求(F_i)呢?
来看一幅图~
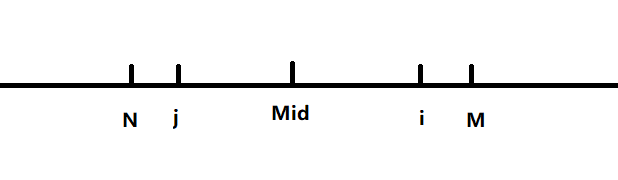
其中,(j)表示(i)关于(Mid)的对称点,(N)表示(M)关于(Mid)的对称点,且(M)=(Mid)+(F_{Mid})
具体来说,(M)就是以(Mid)为中心的最长回文右边界,(i)为当前所求编号。
如果(i<M)(如图),显然有(F_i)=min((F_j),(j-N))
现在知道(N) ~ (Mid)这段与(Mid) ~ (M)这段关于(Mid)对称,且(j-F_j) ~ (j)这段与(j)~(j+F_j)这段关于(j)对称,那么显然有:
①当(j-F_j>=N时),(i-F_j) ~ (i)这段与(i) ~ (i+F_j)这段关于(i)对称
②当(j-F_j<N时),(Mid) ~ (i)这段与(Mid)~(M)这段关于(i)对称
这样以后就可以在O(1)的时间复杂度内知道(i-F_i) ~ (i+F_i)必定为回文字符串,那么再从此向外暴力寻找,就可以得到(F_i)的最终值
若最终的(F_i+i>M),那么为了让后面的(F)值可以更快地求出,我们需要更新(Mid)与(M)值,代码如下:
if(F[i]+i>M)
M=F[i]+i,Mid=i;
三、蒟蒻的代码展示
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=11000010;
char s[N*2];
int F[N*2],ans,pl;
void readn()
{
char ch=getchar();
s[0]='S',s[1]='#';pl=1;//注意从1开始
while(ch<'a'||ch>'z')ch=getchar();
while(ch>='a'&&ch<='z')s[++pl]=ch,s[++pl]='#',ch=getchar();
s[++pl]='�';
}
int main()
{
readn();
for(int i=0,M=0,Mid=0;i<=pl;i++)
{
if(M>i)F[i]=min(F[(Mid<<1)-i],M-i);
else F[i]=1;
while(s[i-F[i]]==s[i+F[i]])F[i]++;
if(F[i]+i>M)M=F[i]+i,Mid=i;
ans=max(ans,F[i]-1);
}
printf("%d
",ans);
return 0;
}
//**月雩·薇嫭**