前缀和例题

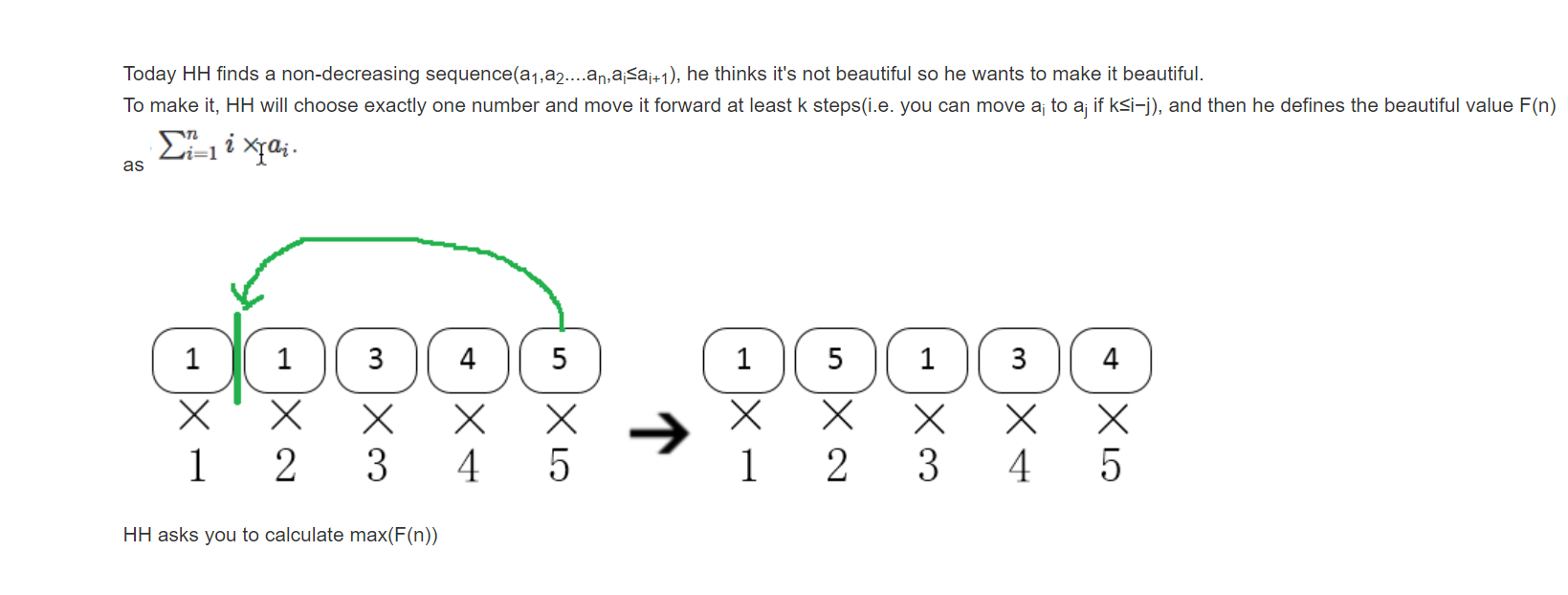
首先我们要注意到：序列是非递减序列，由此我们可以得到一个消息：当一个数往前挪的时候，挪k个一定比挪k+1个要优。然后：挪最后一个未必是最优的，从样例就可以看出来。这样我们就需要枚举挪哪一个。如果每次枚举然后求和的话复杂度是n^2的，所以说前缀和真是个好东西。假如把第x个数向前挪k个，那么从x往后和x-k往前的数，他们对数列的贡献是不变的，因为他们的位置没有变。所以我们可以先预处理出来初始序列的优美值，然后，[x-k,x-1]这k个数整体向后挪了一个，每个人的贡献值都是比之前多了一个本身，我们处理处不加权的前缀和加一个这段的值就可以了，最后是第x个数，他的值a[x]*k，这样每次o（1）算出序列的优美度，枚举下来就是o（n）的。

#include<iostream>
#include<cstdio>
#define ll long long
using namespace std;
const int maxn=1e5+5;
ll ans;
int t;
int n,k;
ll a[maxn];
ll s[maxn],ss[maxn];
int main()
{
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&k);
        for(int i=1;i<=n;++i)
            scanf("%d",&a[i]),s[i]=s[i-1]+i*a[i],
            ss[i]=ss[i-1]+a[i];
        ans=0;
        for(int i=k+1;i<=n;++i)
            ans=max(ans,s[n]-i*a[i]+(i-k)*a[i]+ss[i-1]-ss[i-k-1]);
        cout<<ans<<endl;
    }
    return 0;
}