排序算法：选择排序

选择排序的基本思想：每一趟从待排序的记录中选出关键字最小的记录，按顺序放到已排序的记录序列的最后，直到全部排完为止。

1. 简单选择排序

简单选择排序也称作直接选择排序。
算法过程如图：

算法描述：

void SelectSort(SqList &L) {
  for (int i=1; i<L.length; i++) {
    int k = i;
    for (int j=i+1; j<=L.length; j++) {  // 选择后面序列中最小的值
      if (L[j] < L[k]) k = j;
    }
    if (k != i) {  // 交换L[i]和L[k]
      int temp = L[i];
      L[i] = L[k];
      L[k] = temp;
    }
  }
}

算法分析：
时间复杂度：(O(n^2))
空间复杂度：(O(1))

算法特点：

1. 选择排序本身是种稳定的排序方法，但图中表现出不稳定的现象，这是由于所采用的“交换记录”的策略所造成的的，改变策略，可以写出不产生“不稳定现象”的选择排序算法。
2. 可用于链式结构
3. 移动记录次数较少，当每一记录占用空间较多时，此方法比直接插入排序快。

2. 树形选择排序

树形选择排序，又称锦标赛排序。
算法过程如图所示：

这种排序方法尚有辅助存储空间较多、和“最大值”进行多余的比较等缺点。
为了改进这个缺点，威洛姆斯在1964年提出了另一种形式的选择排序————堆排序。

3. 堆排序

堆排序是一种树形选择排序。
堆实质上是满足如下性质的完全二叉树：树中所有非终端结点的值均不大于（或不小于）其左、右孩子结点的值。

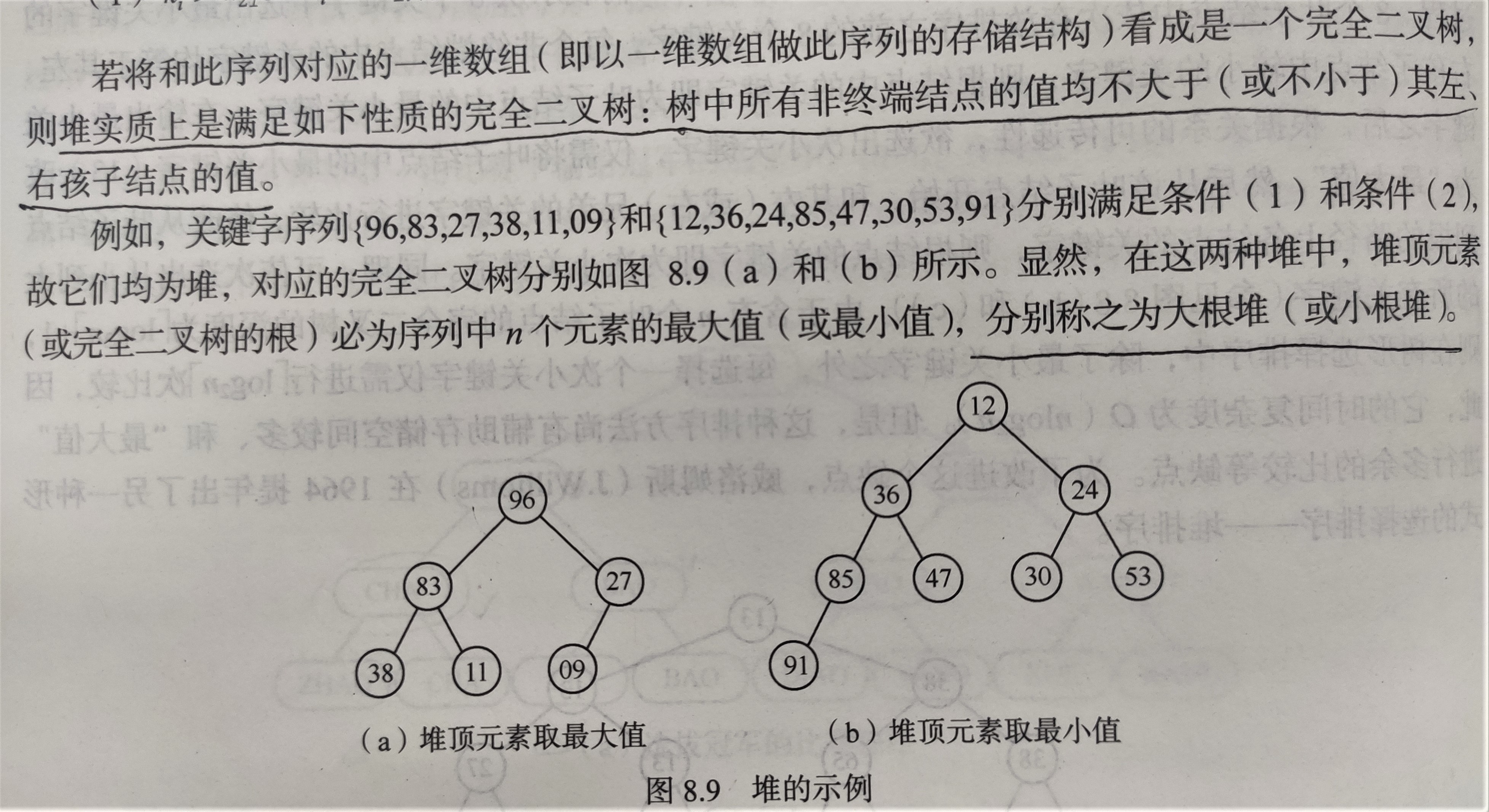
实现堆排序需要解决如下两个问题：
（1）建初堆：如何将一个无序序列建成一个堆？
（2）调整堆：去掉堆顶元素，在堆顶元素改变之后，如何调整剩余元素成为一个新的堆？

1. 调整堆
调整堆过程如图：

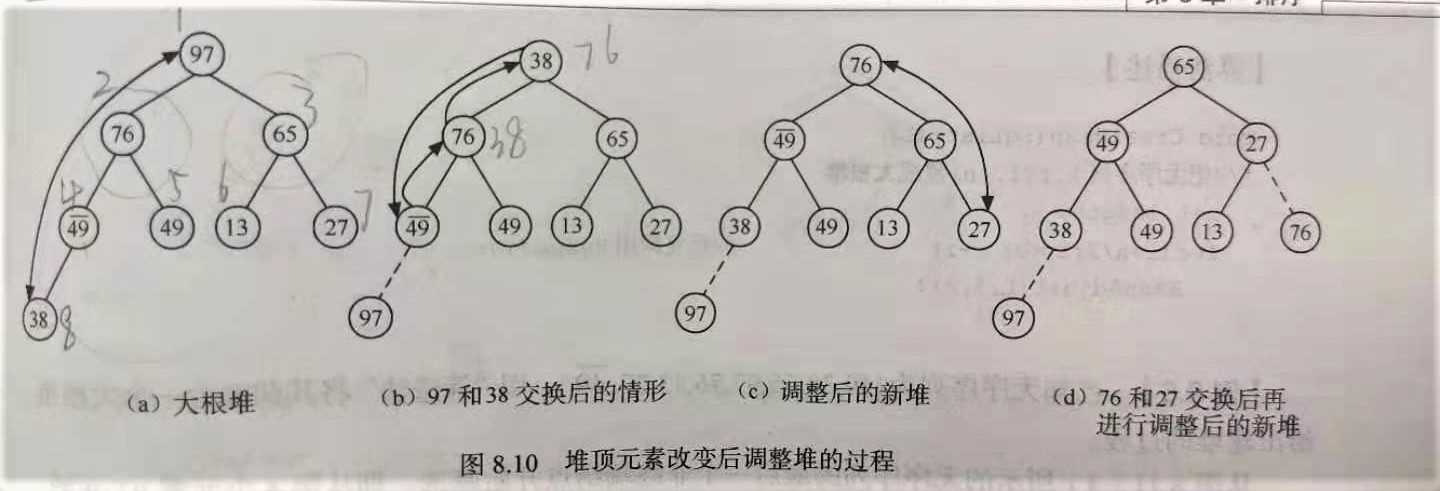
上述过程就像过筛子一样，把较小的关键字逐层筛下去，较大的关键字逐层选上来。因此，称此方法为“筛选法”。

筛选法调整堆算法描述：

void HeapAdjust(SqList &L, int s, int m) {
  int c = L[s];
  for (int j=2*s; j<=m; j*=2) {
    if (j<m && L[j].key < L[j+1].key) j++;  // j为key较大的记录的下标
    if (r.key >= L[j].key) break;
    L[s] = L[j];
    s = j;
  }
  L[s] = c;
}

2. 建初堆
只有一个结点的树必是堆；而在完全二叉树中，所有序号大于(lfloor)(frac{n}{2})( floor)的节点都是叶子，因此只需利用筛选法，从最后一个非叶子结点(lfloor)(frac{n}{2})( floor)开始，依次将(lfloor)(frac{n}{2})( floor)、(lfloor)(frac{n}{2})( floor-1)...、1为序号的节点作为根，分别调整其为堆即可。
建初堆算法描述：

void CreatHeap(SqList &L) {  // 把无序序列L[1, ..., n]建成大根堆
  int n = L.length;
  for(int i=n/2; i>0; i--) {
    HeapAdjust(L, i, n);
  }
}

3. 堆排序算法
堆排序的过程：

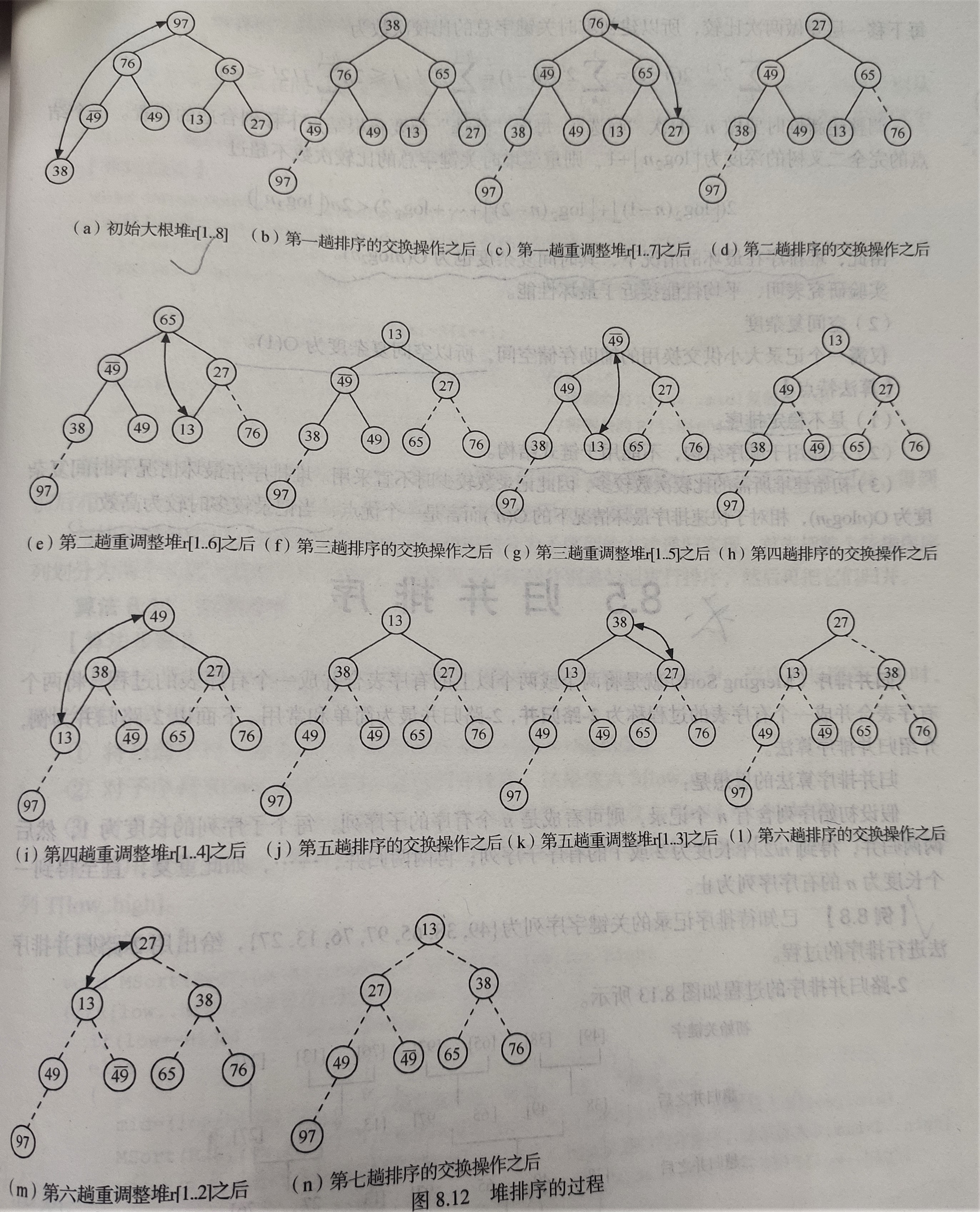
算法描述：

void HeapSort(SqList &L) {
  CreatHeap(L);
  for (int i=L.length; i>1; i--) {
    x = L[1];
    L[1] = L[i];
    L[i] = L[1];
    HeapAdjust(L, 1, i-1);
  }
}

算法分析：
时间复杂度：(O(nlog_2n))
空间复杂度：(O(1))

算法特点：
（1）不稳定排序
（2）只能用于顺序结构，不能用于链式结构
（3）初始建堆需要的比较次数较多，因此 记录数较少时不宜采用。堆排序在最坏情况下时间复杂度为(O(nlog_2n))，相对于快速排序最坏情况下(O(n_2))而言是个优点， 当记录较多时较为高效。