交换排序的基本思想是:两两比较待排序记录的关键字,一旦发现两个记录不满足次序要求时则进行交换,直到整个序列全部满足要求为止。
1. 冒泡排序
冒泡排序是一种最简单的交换排序算法,通过两两比较相邻记录的关键字,使关键字小的记录如气泡一般逐渐往上“漂浮”(左移),关键字大的记录如石块一样逐渐向下“坠落”(右移)。
冒泡排序过程如图
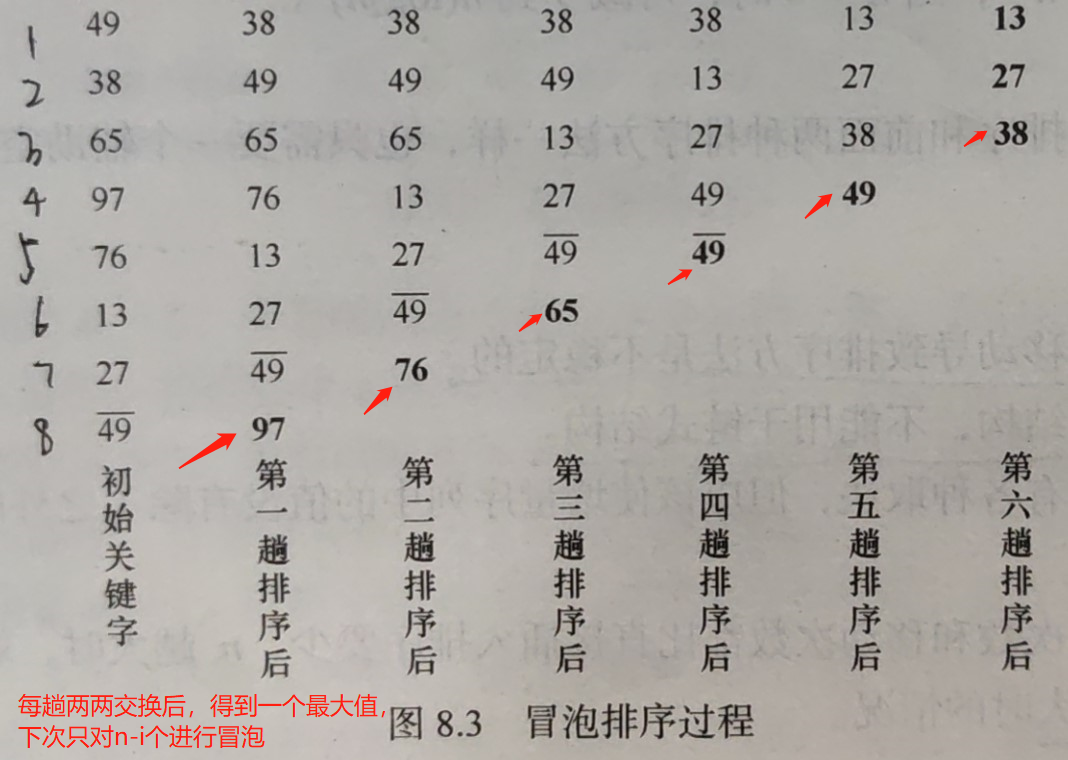
算法描述:
void BubbleSort(SqList &L) {
m = L.length - 1;
flag = 1; // 用来标记某一趟是否发生交换
while ((m > 0) && (flag == 1)) { // 比较多少趟
flag = 0; // 如果本趟排序没有发生交换
for(int i=1; i<=m; i++) { // 每趟比较多少次
if (L[i] > L[i+1]) {
flag = 1;
int temp = L[i];
L[i] = L[i+1];
L[i+1] = temp;
}
}
m--;
}
}
算法分析:
时间复杂度:(O(n^2))
空间复杂度:(O(1))
算法特点:
(1)稳定排序
(2)可用于链式存储结构
(3)移动次数较多,算法平均时间性能比直接排序差。当初始记录无序,n较大时,此算法不宜采用。
2. 快速排序
冒泡排序一次相邻交换只能消除一个逆序,如果能通过两个(不相邻)的一次交换,消除多个逆序,可大大加快排序速度。
快速排序一次交换可能消除多个逆序。
快速排序算法过程如图:

step1:任选一个记录作为枢轴,如选第一个记录,将枢轴记录暂存到r[0],附设low和high指针,初始分别指向下界和上界。
step2:从表最右侧向左搜索,找到第一个小于枢轴pivotkey的记录,将其移到low处。具体操作:当low<high时,若high大于privotkey,左移high,否则high记录放到low处。
step3:从表最左侧向右搜索,找到第一个大于枢轴pivotkey的记录,将其移到high处。具体操作:当low<high时,若low小于privotkey,右移low,否则low记录放到high处。
step4:重复step2和step3直到low=high。此时low或high的位置就是枢轴在此趟排序中的最终结果,原表被分成两个子表。
(思考:枢轴的位置如果任意选,非第一个记录,算法是不是会有所差别?)
算法描述:
void QuickSort(SqList &L) {
QSort(L, 1, L.length);
}
void QSort(SqList &L, int low, int high) {
if (low < high) {
int privotloc = Partition(L, low, high);
QSort(L, low, privotloc -1);
QSort(L, privotloc + 1, high);
}
}
int Partition(SqList &L, int low, int high) {
L[0] = L[low]; // 用子表的第一个记录做枢轴记录
while (low < high) {
while (low < high && high > L[0]) high--;
L[low] = L[high];
while (low < high && low < L[0]) low++;
L[high] = L[low];
}
L[low] = L[0];
return low;
}
Java实现(牛客排序笔试题):
import java.util.*;
public class Solution {
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
* 将给定数组排序
* @param arr int整型一维数组 待排序的数组
* @return int整型一维数组
*/
public int[] MySort (int[] arr) {
// write code here
// 冒泡排序(运行超时)
// int n = arr.length;
// for(int i=0; i<n-1; i++) { // 比较多少趟
// for(int j=0; j<n-i-1; j++) { // 每趟比较多少次
// if(arr[j] > arr[j+1]) {
// int temp = arr[j];
// arr[j] = arr[j+1];
// arr[j+1] = temp;
// }
// }
// }
// return arr;
// 快速排序(内部排序中,n个数大时,最快的一种排序方法)
int n = arr.length;
if(n == 0) return arr;
return QSort(arr, 0, n - 1);
}
public int[] QSort(int[] arr, int low, int high){
if(low < high) {
int pivoteIndex = partition(arr, low, high);
QSort(arr, low, pivoteIndex - 1); // 为这个元素前的部分排序
QSort(arr, pivoteIndex + 1, high); // 为这个元素后的部分排序
}
return arr;
}
// 返回枢轴位置(为一个元素排好了序,返回这个元素所在的位置)
public int partition(int[] arr, int low, int high) {
int pivote = arr[low]; // 注意这里是arr[low]作为枢轴,不是arr[0]
while(high > low) {
while(arr[high] >= pivote && high > low) { // 注意是arr[high]与pivote的比较,不是high与pivote的比较
high--;
}
arr[low] = arr[high];
while(arr[low] <= pivote && high > low) { // 同样注意与pivote的比较对象
low++;
}
arr[high] = arr[low];
}
arr[low] = pivote;
return low;
}
}
算法分析:
时间复杂度分析:(O(nlog_2n))
空间复杂度分析:需要一个递归栈,最好(O(log_2n)),最坏(O(n))
算法分析:
- 非顺次移动导致排序方法不稳定
- 需要定位上下界,适合用于顺序结构,很难用于链式结构
- n较大时,在平均情况下 快速排序是所有内部排序中最快的一种,所以其适合初始记录无序、n较大时的情况(尤其不适合有序)。