容斥原理
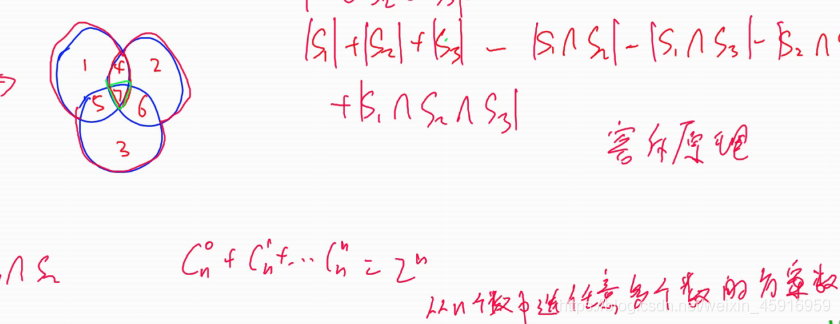
等式左边看作从集合中 所有选任意n个区域的方案,右边表示 每个区域选与不选 的所有方案,是同一个东西。
假设有k个圈圈,中间的区域开始被算了C(1,k)次,之后减去了C(2, k)次,之后又加上C(3, k)次……最后加上(-1)k-1C(k, k) = 1;
这也是一个组合恒等式,有很多个组合恒等式,搜一下。
题目:能被整除的数
思路:容斥原理
公式的实现方式: 位运算 枚举所有的选法;;
每个同等级的圈圈都可以看做是在这k个数里面选择n合数的组合数
从n个集合当中选任意多个集合
答案
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 20;
int p[N];
int main()
{
int n, m;
cin >> n >> m;
for (int i = 0; i < m; i ++ ) cin >> p[i];//输入所有的p
int res = 0;//结果
for (int i = 1; i < 1 << m; i ++ )//每个i代表一种取法,每种取法代表了一个圈圈,每个圈圈可以看做是k个圈圈相交得到的圈圈
{
int t = 1, s = 0;//s算1的个数也就是算这个圈圈是由几个圈圈橡胶垫得到的圈圈
for (int j = 0; j < m; j ++ )
if (i >> j & 1)
{
if ((LL)t * p[j] > n)//要是大于n的话,说明这种数根本不存在。
{
t = -1;//不用算了。
break;
}
t *= p[j];//倍数
s ++;//算1的个数
}
if (t != -1)//
{
if (s % 2) res += n / t;//如果是数个的话就加上
else res -= n / t;//如果是偶数个的话就减去
}
}
cout << res << endl;
return 0;
}