算法：
一、 将中缀表达式转换成后缀表达式算法：
1、从左至右扫描一中缀表达式。
2、若读取的是操作数，则判断该操作数的类型，并将该操作数存入操作数堆栈
3、若读取的是运算符
(1) 该运算符为左括号"("，则直接存入运算符堆栈。
(2) 该运算符为右括号")"，则输出运算符堆栈中的运算符到操作数堆栈，直到遇到左括号为止。
(3) 该运算符为非括号运算符：
(a) 若运算符堆栈栈顶的运算符为括号，则直接存入运算符堆栈。
(b) 若比运算符堆栈栈顶的运算符优先级高或相等，则直接存入运算符堆栈。
(c) 若比运算符堆栈栈顶的运算符优先级低，则输出栈顶运算符到操作数堆栈，并将当前运算符压入运算符堆栈。
4、当表达式读取完成后运算符堆栈中尚有运算符时，则依序取出运算符到操作数堆栈，直到运算符堆栈为空。
二、逆波兰表达式求值算法：
对后缀表达式求值比直接对中缀表达式求值简单。在后缀表达式中，不需要括号，而且操作符的优先级也不再起作用了。可以用如下算法对后缀表达式求值：
- 初始化一个空堆栈
- 从左到右读入后缀表达式
- 如果字符是一个操作数，把它压入堆栈。
- 如果字符是个操作符，弹出两个操作数，执行恰当操作，然后把结果压入堆栈。如果您不能够弹出两个操作数，后缀表达式的语法就不正确。
- 到后缀表达式末尾，从堆栈中弹出结果。若后缀表达式格式正确，那么堆栈应该为空。
功能一的实现：
效果图如下：
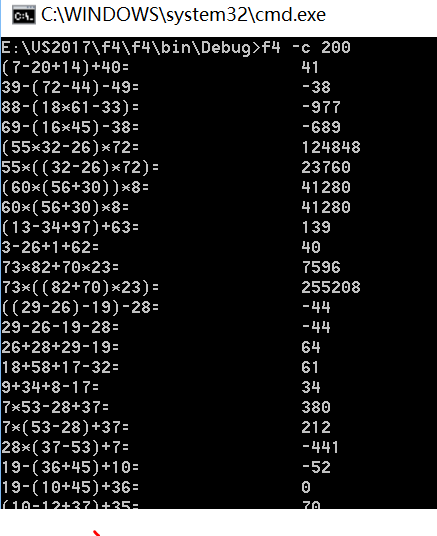
参考了一个博客：计划写出3个主函数来实现这个功能，今天先写了一些其余的小函数：
using System;
using System.Collections;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
//author： yy
//time:17/10/05
namespace f4
{
class arithMetic
{
static void Main(string[] args)
{
//主函数
}
class work
{
int[] numbers;
string[] optionsArray = new string[] { "+", "-", "*", "/", "(", ")" };//运算符号和括号
string[] fourOptions = new string[] { "+", "-", "*", "/" };//四则运算符
}
//运算符优先级
static int privority(string str)
{
int pri = 0;
switch (str)
{
case "+": pri = 0; break;
case "-": pri = 0; break;
case "*": pri = 1; break;
case "/": pri = 1; break;
case "(": pri = 2; break;
case ")": pri = 2; break;
}
return pri;
}
//四则运算
static int[] OptionsArithMetic(string firOps, string secOps, string ops)
{
int first= int.Parse(firOps);
int second = int.Parse(secOps);
int res = 0;
switch (ops)
{
case "+": res = first + second; break;
case "-": res = first - second; break;
case "*": res = first * second; break;
case "/": res = first / second; break;
}
return res;
}
//分割表达式，并入队列
public Queue<string> SplitExpress(string express)
{
}
//中序表达式转换为后序表达式
public List<string> InorderToPostorder(Queue<string> q)
{
}
//计算后序表达式
public bool IsResult(List<string> PostorderExpress, out decimal result)
{
}
先写个博客证明一下自己的工作，逃：）
enmmmmmm，写了函数随机生成20道四则运算题目：
//随机生成20道运算题
static void RandOut()
{
Random rd = new Random();
int num1, num2, num3, num4;
char[] fourOptions = new char[] { '+', '-', '*', '/' };//四则运算符
int i, j, charnum;
for (i = 0; i < 20; i++)
{
num1 = rd.Next();
num2 = rd.Next();
num3 = rd.Next();
num4 = rd.Next();
charnum = rd.Next() % 4;
for (j = 0; j < 3; j++)
{
if (charnum == 0)
{
fourOptions[j] = '+';
}
if (charnum == 1)
{
fourOptions[j] = '-';
}
if (charnum == 2)
{
fourOptions[j] = '*';
}
if (charnum == 3)
{
fourOptions[j] = '/';
}
Console.WriteLine(num1 + fourOptions[j] + num2 + fourOptions[j] + num3 + fourOptions[j] + num4);
}
}
}
下面是实现将遍历中序表达式转化为后序表达式：
//是否为数字，判断是否为整数字符串
static bool isNumber(string message)
{
//判断是否为整数字符串
//是的话则将其转换为数字并将其设为out类型的输出值、返回true, 否则为false
int result = -1; //result 定义为out 用来输出值
try
{
result = Convert.ToInt32(message);
return true;
}
catch
{
return false;
}
}
//判断操作符优先级大小
static bool comparePriority(string op1, string op2)
{
return getPriorityValue(op1) > getPriorityValue(op2);
}
private static int getPriorityValue(string op1)
{
throw new NotImplementedException();
}
static Stack<string> changeExpression(List<string> beforeExps)
{
Stack<string> operand = new Stack<string>();//操作数
Stack<string> opertor = new Stack<string>();//操作符
//遍历中序表示
int length = beforeExps.Count;
int len = opertor.Count;
//判断是否为操作数
for (int i = 0; i < length; i++)
{
string c = beforeExps[i];
if (isNumber(c))
{
//操作数 存在操作数栈
operand.Push(c);
}
else
{
//为运算符
//若运算符为"("直接存入到运算符栈中
if (c == "(")
{
opertor.Push(c);
}
else if (c == ")")
{
//该运算符为右括号")"，则输出运算符堆栈中的运算符到操作数堆栈，直到遇到左括号为止。 将"("出栈
while (opertor.Peek() != "(")
{
string stringvalue = opertor.Pop();
operand.Push(stringvalue);
}
opertor.Pop();
}
else
{
// 该运算符为非括号运算符：
//考虑栈顶为空的情况
if (len <= 0)
{
opertor.Push(c);
continue;
}
// (a) 若运算符堆栈栈顶的运算符为括号，则直接存入运算符堆栈。
////符合为左括号 直接存入运算符
if (opertor.Peek() == "(")
{
opertor.Push(c);
}
else
{
//(b) 若比运算符堆栈栈顶的运算符优先级高或相等，则直接存入运算符堆栈。
if (comparePriority(c, opertor.Peek()))
{
opertor.Push(c);
}
else
{
// (c) 若比运算符堆栈栈顶的运算符优先级低，则输出栈顶运算符到操作数堆栈，并将当前运算符压入运算符堆栈。
string stringvalue = opertor.Pop();
operand.Push(stringvalue);
opertor.Push(c);
}
}
}
}
}
//4、当表达式读取完成后运算符堆栈中尚有运算符时，则依序取出运算符到操作数堆栈，直到运算符堆栈为空。
while (len > 0)
{
string stringvalue = opertor.Pop();
operand.Push(stringvalue);
}
//反转operand 获取正常的后缀表达式
Stack<string> resultSt = new Stack<string>();
while (len > 0)
{
string stringvalue = operand.Pop();
resultSt.Push(stringvalue);
}
return resultSt;
}
要求1 参考《构建之法》第4章两人合作，结对编程上述功能，要求每人发布随笔1篇 (代码是共同完成的，博客是分别完成的)。 (1) 给出每个功能的重点、难点、编程收获。(2)给出结对编程的体会，以及 (3) 至少5项在编码、争论、复审等活动中花费时间较长，给你较大收获的事件。 (10分)
（1）重点难点以文档形式在coding.net上，链接为：https://coding.net/u/Dawnfox/p/f4/git/blob/master/doc/%E5%9B%9B%E5%88%99%E9%9C%80%E8%A6%81%E6%B3%A8%E6%84%8F%E7%9A%84%E5%9C%B0%E6%96%B9V1.1.docx
（2）本次结对编程我的搭档是冉华同学，在这次结对编程的过程中我收获良多，之前我拿到题目后非常焦急，因为发现功能一就需要用到逆波兰表达式，但是之前编译原理学习的相关知识已经忘了，而且接触c#的时间也不过3个星期，感到一头雾水无从下手。然而冉华告诉我，拿到题目之后最好不要直接就开始写，因为心里没有一个完成计划与标准，在写作业的过程中容易顾此失彼，这样做收获很有限。听从了冉华同学的建议，我们在开始写作业之前做了时间较长的前期准备，比如：挖掘题目的隐含信息、讨论算法思想与代码编写顺序等，因为前3周的作业我都是在实验室的机器上完成的，这个国庆假期前几天实验室没有开门，所以在我自己的电脑上安装环境也花费了一定的时间。在前几天，主要通过阅读博客和问同学知道了如何在vs2017环境下进行单元测试，后来在编写程序之前我阅读了大量的博客，了解了四则运算实现的算法过程，尝试了编写功能一其中的几个函数，并且通过看冉华同学编写代码了解了有经验的同学是如何写程序的，收获了很多。我感受到基础的重要性，在编写程序的过程中会引用到常用的库函数与方法，虽然不可能完全记得这些但是最好有个印象，常用的方法一定要了解最好能够熟练使用，当然这需要大量的练习来不断地巩固，在完成一个个小任务后可以收获满足感，这样就有动力继续进行更多的编程练习。 最后，感谢冉华同学在本次作业的完成中给我的指导与帮助。
（3）a.首先在确定需求的时候产生了分歧，是自动生成20道题目还是手动输入
b.在学习单元测试的时候花费的时间比较长，从安装插件到学习如何测试花费3小时
c.学习逆波兰表达式的实现，冉华同学给我讲解的时间较长，大约2小时
d.自己尝试编写四则运算求值部分代码，花费时间较长
e.在最后进行最终单元测试的时候，我的vs2017出问题了，有些配置出问题了，现在正在看，已经花费2.5小时
要求2 给出照片1张，包括结对的2位同学、工作地点、计算机，可选项包括其他能表达结对编程工作经历的物品或场景。 (5分)
