在这篇博客中我们讨论一下谷歌pagerank算法。这是参考的原博客连接:http://blog.jobbole.com/71431/
https://blog.csdn.net/weixin_43378396/article/details/90322422
PageRank的Page可是认为是网页,表示网页排名,也可以认为是Larry Page(google 产品经理),因为他是这个算法的发明者之一,还是google CEO(^_^)。PageRank算法计算每一个网页的PageRank值,然后根据这个值的大小对网页的重要性进行排序。它的思想是模拟一个悠闲的上网者,上网者首先随机选择一个网页打开,然后在这个网页上呆了几分钟后,跳转到该网页所指向的链接,这样无所事事、漫无目的地在网页上跳来跳去,PageRank就是估计这个悠闲的上网者分布在各个网页上的概率。
互联网中的网页可以看出是一个有向图,其中网页是结点,如果网页A有链接到网页B,则存在一条有向边A->B,下面以一张简单的图为例:
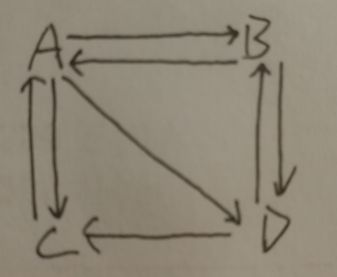
这个例子中有四个网页,如果当前在A网页,那么上网的人将会各以1/3的概率跳转到B、C、D,这里的3表示A有3条出链,如果一个网页有k条出链,那么跳转任意一个出链上的概率是1/k,同理D到B、C的概率各为1/2,而B到C的概率为0。一般用转移矩阵表示上网者的跳转概率,上面示例图对应的转移矩阵如下:
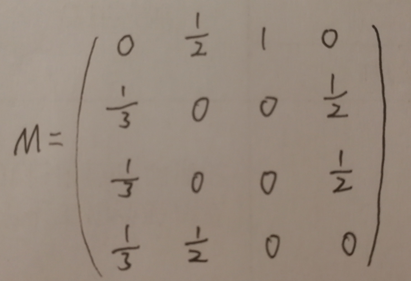
初试时,假设上网者在每一个网页的概率都是相等的,即1/n,于是初试的概率分布就是一个所有值都为1/n的n维列向量V0,用V0去右乘转移矩阵M,就得到了第一步之后上网者的概率分布向量MV0,(nXn)*(nX1)依然得到一个nX1的矩阵。下面是V1的计算过程:
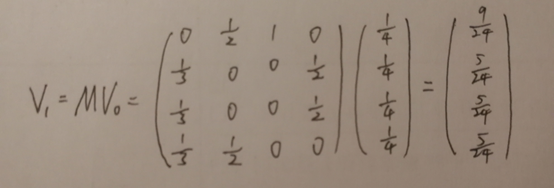
得到了V1后,再用V1去右乘M得到V2,一直下去,最终V会收敛,即Vn=MV(n-1),上面的图示例,不断的迭代,最终V=[3/9,2/9,2/9,2/9]’
但是上面过程,我们忽略了一个问题,那就是上网者有的时候会离开现在的网页,在浏览器的地址随机输入一个地址。于是我们对算法进行改进,在地址栏输入而跳转到各个网页的概率是1/n。假设上网者每一步查看当前网页的概率为a,那么他从浏览器地址栏跳转的概率为(1-a),下面我们假设a=0.8,于是原来的迭代公式转化为:
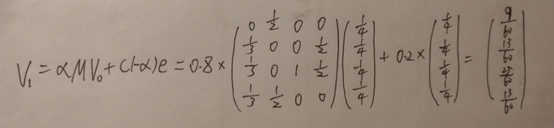
重复迭代下去,得到V=[3/9,2/9,2/9,2/9]’