修正:
样本统计数和样本统计量之间的关系是什么?
样本统计量是一个变量,而样本统计数是该变量对应的数值。样本统计量也是样本统计数,参数也是参量。
生物统计学和统计学都包含两部分是什么?
统计学的基本内容包括(统计描述)和(统计推断)两大部分。
生物统计学的基本内容包括(试验设计)和(统计分析)两大部分。
生物统计学的发展过程经历了哪3个阶段?
(古典记录统计学)、(近代描述统计学)和(现代推断统计学)
什么是变量的性质?
就是就结果的数字而言,这些数字具有哪些性质一直相对的是“研究对象的性状特征”。
随机变量在不同的条件下由于偶然因素影响,可能取各种
随机变量
不同的值,故其具有不确定性和随机性,但这些取值落在某个范围的概率是一定的,此种变量称为随机变量。随机变量可以是离散型的,也可以是连续型的。如分析测试中的测定值就是一个以概率取值的随机变量,被测定量的取值可能在某一范围内随机变化,具体取什么值在测定之前是无法确定的,但测定的结果是确定的,多次重复测定所得到的测定值具有统计规律性。随机变量与模糊变量的不确定性的本质差别在于,后者的测定结果仍具有不确定性,即模糊性。
变异数是什么?
本文介绍的是变异数,又称方差、变方。
变量的分布具有两个明显基本特征是什么?
集中性特征和离散性特征。
特征和特征数是什么?
Eg:特征是离散性特征,而离散性特征数是变异数。特征数包括平均数,方差(变异数),极差,方差,标准差。
计数变量是什么?
计数变量是定性变量,计量资料是定量变量,即计量资料是数值变量。
定性变量(3,4)和定量变量(1,2)与连续变量(1,2,3)与非连续变量(1,2,3,4)是两个不同体系。

样本平均数的标准误和样本平均数的标准差分别是什么?
这两个是同一个东西。
标准误,即样本均数的标准差,是描述均数抽样分布的离散程度及衡量均数抽样误差大小的尺度,反映的是样本均数之间的变异。标准误不是标准差,是多个样本平均数的标准差。
独立和互斥的关系?
两个事件互斥是指两个事件不可能同时发生,两个事相互独立是指一个事件的发生与否对另一个事件发生的概率没有影响。 它们虽然都描绘了两个事件间的关系,但所描绘的关系是根本不同的。 若A、B互斥,且P(A)>0 ,P(B)>0,则它们不可能互相独立,因为A发生的条件下,B不可能发生,即 ,所以A、B不是互相独立。
独立是指A、B两个事件可以同时发生也可以不同时发生,两个事件发生的概率不会因为某事件发生而发生。所以,独立必然不互斥,互斥必然不独立。
二项分布的由来是什么?
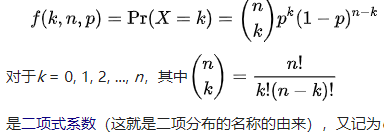
什么是方差齐性?
不是每个样本方差相同,而是不同样本所在的不同总体的方差相同。
方差齐性检验(Homogeneity of variance test)是数理统计学中检查不同样本的总体方差是否相同的一种方法。 其基本原理是先对总体的特征作出某种假设,然后通过抽样研究的统计推理,对此假设应该被拒绝还是接受作出推断。

离差是什么?
离差(deviation)有两个义项,可以指一个观测值或测验分数与特定的参照点(如平均数、中数等)之间的差距,亦称“离均差”[离差(dispersion)是随机变数的值(即一组数据)关于某个中心值(通常取为数学期望*)偏离或散布的离散程度的一种标志。它通常用标准差来度量,也可以用平均偏差或平均差来度量];也可以指直线关于点的离差。

进行两因素或多因素试验时,通常应设置重复的理由?
不是只要不研究交互作用便不用设置重复了,而是只要研究两个因素以上都要设置重复值,否则无法研究究竟有没有交互作用,研究主效应。