PCA:主成分分析
相关矩阵,找特征值,找每个特征值对应特征向量,即组成主组成式子:

每个式子指向一个结果y,找一条线将这些y分开。有11个变量就有11个新坐标轴,通过点到直线距离来区分。
信息必须集中在前几个主成分上。比如PC1表示3个变异。
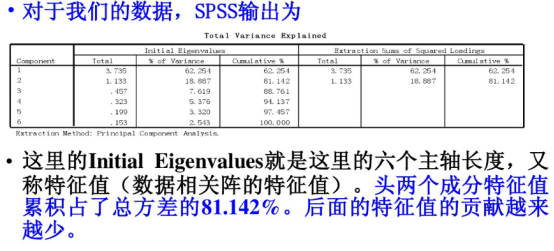
主成分分析的前提是原始数据不能不同x指向同一个y。
主成分分析不能用来代表某一组因素的共同作用。
PCA是一类因子分析,在特征值提取时可以选择不同算法。

取第一列和第二列主成分,可以得到二维图:
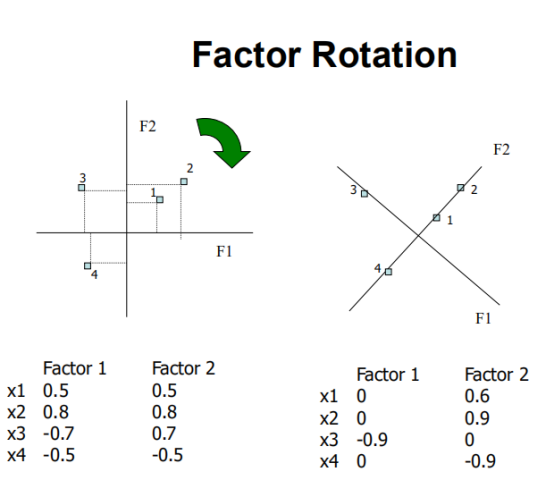
通过改变坐标轴可将差异表达的更清楚。
PCA和cluster区别是Cluster目标是将y分类,PCA将特征值分类。
对应分析:卡方分析反映出期望与观测值的差异,即是信息点,行列之间的不规律性。对卡方矩阵做主成分分析,原矩阵和转置后的矩阵都做一遍。所以
PCA与CA的比较:
CA要求原始数据可以不单调,不要求正态。
PCA要求原始数据可以不单调,最后的主成分转化为一个个欧式距离,要求正态。