应用统计学
统计量与抽样分布
精确估计:当总体满足正态分布时。一个样本参数估计,估计总体均值时。
总体方差已知时,用样本均值满足抽样分布来估计,(其中,抽样分布是正态分布,抽样分布均值是总体均值,抽样分布方差是总体方差与样本数的比值)来估计,即如下式:

此方法的进阶版就是将样本均值写成Z分布形式,z分布满足正态分布:

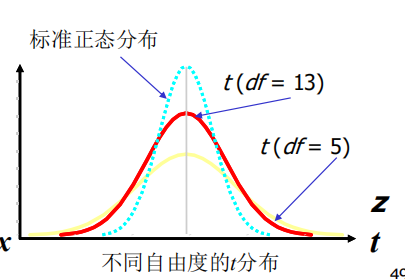
总体方差未知时,用样本均值满足抽样分布来估计,(其中,抽样分布是t分布,抽样分布与将总体均值的关系)来估计(区间估计),即如下式:

一个样本参数估计,估计总体方差时(区间估计)。
总体方差未知时,用样本方差满足抽样分布来估计,(其中,抽样分布是卡方分布,抽样分布与总体方差的关系)来估计(区间估计),即如下式:


二项分布存在参数比率π,用p(样本比率)估计
简单随机抽样要求随机性(即抽到每一个样本的概率相同,抽到每个球概率不同的情况可能发生在抽取者看到红球,便抽取红球),和独立性(每次抽取的样本物理条件保持一致)
抽样分布:抽样分布是依据抽样个数n模拟抽出样本统计量的分布。每一个样本容量保证相同,若每个样本40个做100次,则会得到100个样本均值,所以能够得到100个抽40个能得到该100个样本均值的总体均值,这些估计的总体均值是抽样分布,该抽样分布的期望对于总体均值来说是无差的。

样本均值的标准误差:
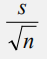
样本均值的标准差:
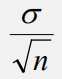
总体标准差:
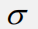
样本标准差:S
粗略估计:当总体未知分布,但是有总体方差时,采用中心极限定理,当抽样个数达到很大时,样本均值的抽样分布近似正态分布:

如果总体是正态分布则样本均值是精确的服从正态分布
