2048游戏控制器
1 evaluate
要用程序来处理就得对现实的问题进行量化,用数字来表示。在2048游戏中,我们的输入是一个棋局,让我们输出一个移动方向,这样我们需要对棋局进行量化,即我们要评估棋局的好坏,用一个score来表示,score越大棋局越好,score越小棋局就越差。
玩过2048后就会知道,一个好的棋局会与这几个方面有关系:
1、数据块的单调性 :monotonous
2、空格数:emptys
3、可合并数 :merges
通过计数单调性monotonous、统计空格数empty和可合并的个数merges我们就能得到我们的评估函数:
score = monotonous*w1 + emtpys * w2 + merges * w3
其中w1、w2、w3是各个要素对评估函数的影响的权重。这个需要手动去调整,也也可以通过演进算法CMA-ES去搜索最优值。
2 算法
有了合理的评估方式我们就可以将当前棋局以四个方向进行移动(up,down,left,right),对移动后的棋局进行评估,得到4个score_left、score_right、score_up、score_down,此时我们会取4个score的最大值score_max = max(score_left,score_right,score_up,score_down)对应的移动方向作为当前棋局的移动方向,但是这样的移动是最优的吗?显然对应当前棋局来说是最优的,但是考虑到未来的可能棋局就不一定是最优的了,因为我们移动后电脑会随机加入一个2或4的块(概率为别为0.9和0.1),电脑的这个操作(棋手对弈也一样)会改变棋局,影响后续的移动。所以,如果只对移动一次后的棋局进行评估就决定移动方向只能得到当前最好的棋局,但是后续的棋局好不好就不能保证了,说不定电脑在某个特殊点放置一个块,后面就game over了。为了到达最高分,我们即要保证当前的移动不坏,同时也要考虑后续的情况,这样才能不断的保持一个好的棋局,使自己不断移动下去,取得最高分,(移动的次数越多分就越高),考虑长远收益。
举例说明当前最优,但长远来看不是最优:
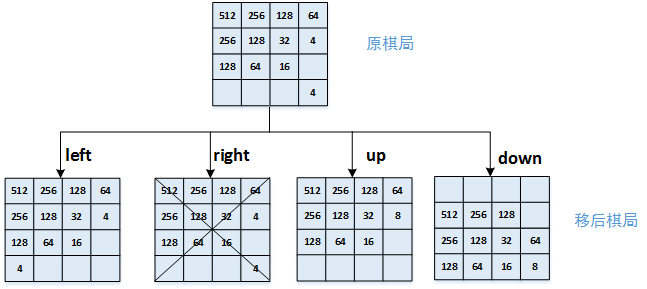
上图中,在原棋局的基础上进行4个方向的移动,分别得到4个移动后的棋局,用我们上面的的evaluate方法对移动后的棋局进行评分,我们很容易就能知道up移动后的棋局得分会最高。
如果我们选择up,那么电脑(对手)会随机的放置一个2的块(0.9的概率)或者一个4的块(0.1的概率)会得到如下的棋局
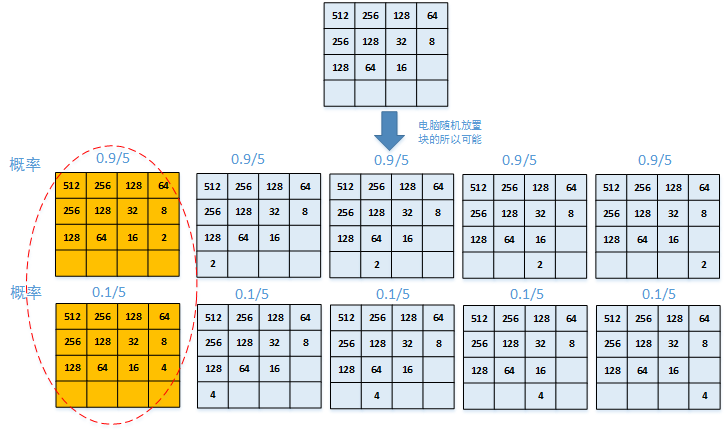
其中出现虚线框中两种棋局的概率是1/5,当出现这个棋局,我们只有一种移动棋局选择,就是down,down以后的棋局单调性就很差了(空格认为是0),可能就是因为我们这一步down就导致后面很快输掉棋局。然而真正导致这种结果的源头却在前几部的移动上,如果起名前一步选择left就完全可避开这种导致满盘皆输的错误移动。这个例子就说明了,当前一步的最好选择可能会导致未来移动的挫折,所以每移动异步需要考虑未来可能出现的棋局,通过大局观的考虑来决定当前怎么移动。
在上面这种考虑未来的情况思想下(求期望),有两种博弈算法相对应,一种是MinMax一种是ExpectiMax
2.1 MinMax
MinMax算法在预测未来棋局的时候,对手下棋后得到的总是一个Min棋局(最坏棋局,对手最优棋局),自己下棋后得到一个Max棋局(自己的最优棋局)
如下图所示,对手和我每次下棋只有两种选择,到底当前选择1下法还是选择2下法呢,当然你会说那种下法的赢的概率大就选那个。如何知道那种赢的概率大呢,当然是棋局越来越好赢的概率就大。
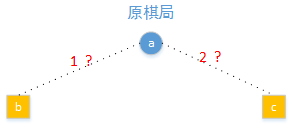
假设选择1下法得到b棋局,同时遍历对手可能的选择得到d和c棋局,更进一步遍历我在d和e棋局下的下法得到i、j、k、l棋局。同样的对2下法也进行同样的操作会得到m、n、o、p
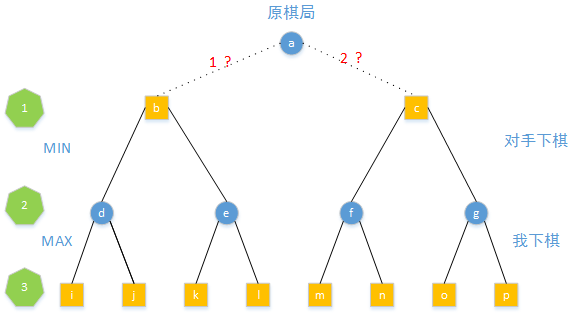
对这8个棋局进行评估分数,假设分值如下
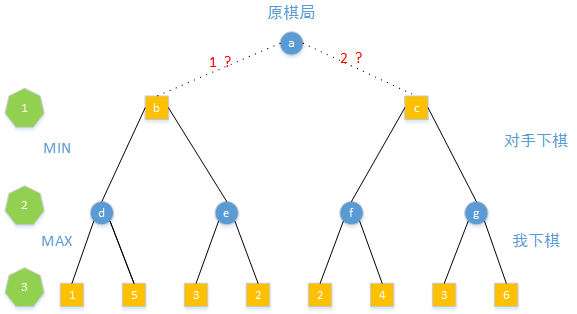
上面从b到4个棋局和从c到4个棋局是遍历的过程,还不知道b移两步后4个棋局的概率分布,这个时候需要从b树和c树的叶子节点进行逆向反推,反推的依据就是棋手(我和对手)选择棋局的分布
| 我的分布 | 选未来好棋局 | 选未来差棋局 |
|---|---|---|
| 概率 | 1 | 0 |
| 对手分布 | 选未来好棋局 | 选未来差棋局 |
|---|---|---|
| 概率 | 0 | 1 |
这里的好与坏是相对于我来说的。选好棋局的概率为1,就是求Max,选差棋局的概率为1,就是求Min.
第3步是我下棋,我只会选择好的棋局,所以从d、e、f、g下棋只会出现得分为5、3、4、6的棋局
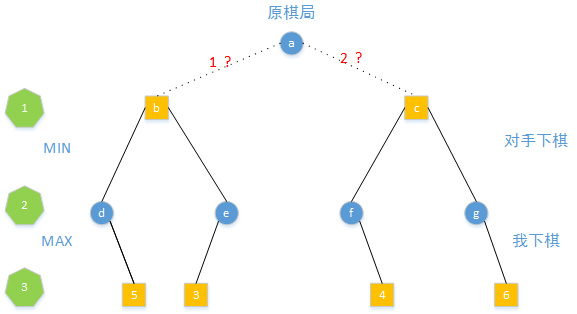
第2步是对手下棋,他只会选择对于我未来差的棋局,所以从b和c棋局只会得到e和f
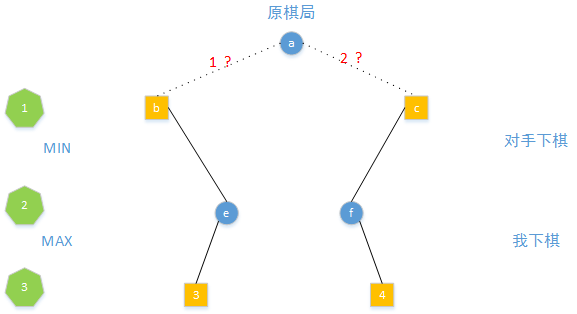
这样我们就预测出了3步以后(未来)的棋局,我们发现如果选择1下法,未来棋局得分是3,选择2下法的话,未来棋局的得分是4,所以我们应该选择2下法。
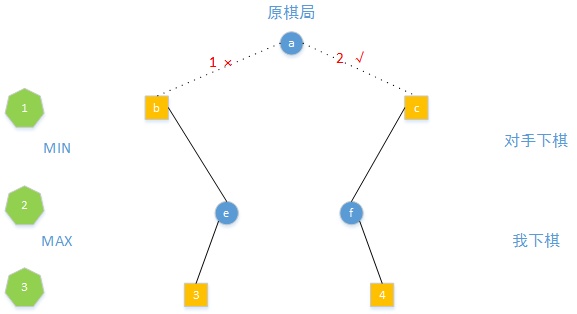
上面我下棋的过程是Max过程,对手下棋是Min过程,就是MaxMin算法的思想。其实就是预测未来棋局的分布,选择当前下法会导致未来出现好棋局的概率大的下法进行下棋。
上面通过一个例子解释什么是MaxMin,为什么要用MaxMin。我们可以把MaxMin的过程用公式表示出来。
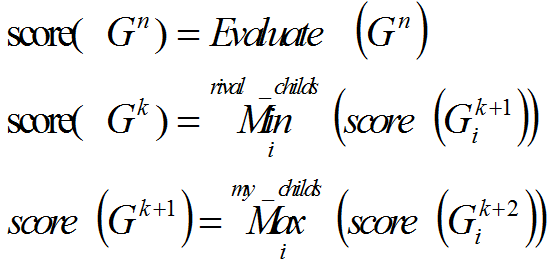
k和n表示预测的深度(第n步后直接使用evaluate的值),rival_childs表示对手在$Gk$棋局时能够得到的所以棋局$G(k+1)_i$,my_childs表示我在$G(k+1)$棋局值能够得到所以棋局$G(k+2)_i$。在对手局的时候,对手选择所以棋局中最差的。在我的棋局时,我会选择最好的棋局。在原始棋局选择哪个棋局作为下一个棋局就是一个求期望的过程,对手棋局的期望是它所以可能棋局最差棋局的得分,我的棋局就是我的所以可能棋局中最好的得分。在计算期望的过程中选先要把棋局往下展开,并在第n步以后对棋局进行评估得到棋局的分数,然后往上计算棋局的期望,最后能得到初始棋局能到达的N个棋局的期望,取则N个棋局最后最好的棋局作为初始棋局的下一关棋局。
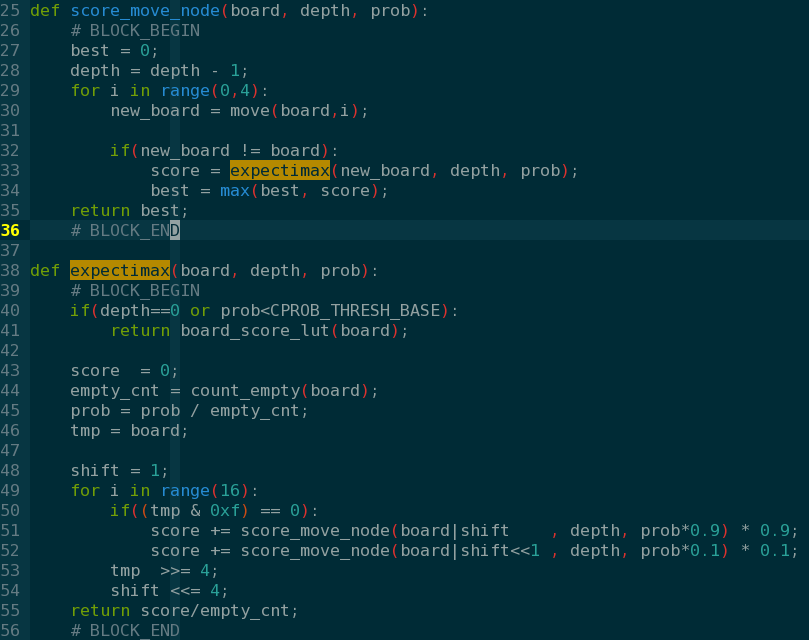
在用程序实现的时候会采用递归的方式来时序,在递归中,分两个步骤,先是递归往深处走,将棋局不断遍历展开,然后是评估最深哪一步得到棋局的评分,然后通过Min和Max不断缩小棋局的个数,最后剩下N个棋局,选择N个棋局中最优的那个对应的下法作为当前棋局的下法是最好的。
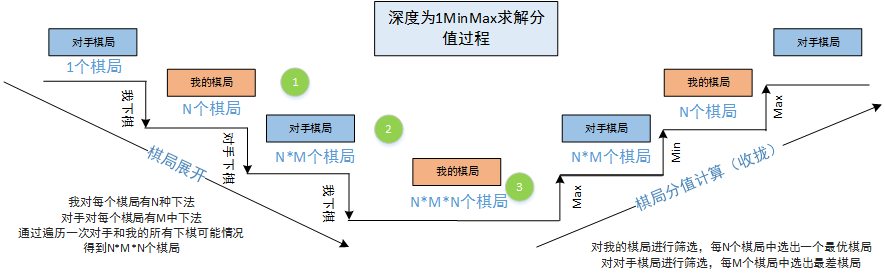
说到根本,博弈的目的不仅要当下占优势,更要在未来占优势,这使得我们需要预测未来棋局的情况,并且选择未来赢的概率最大分支对应的下法作为当下的下法;
预测未来就需要知道事件的分布情况,在下棋的这个博弈游戏中,棋手都倾向于未来棋局好的下法下棋;在MaxMin算法中就比较极端,直接认为棋手都很厉害(对手和自己),每次下棋都是最优的(在evaluate棋局很准确的情况下),对手选择对于我最差的棋局,我选择对于我最好的棋局,且对手选择最差棋局的概率为1,我选择最好棋局的概率也为1。(这套程序与一个差棋手对弈的话长远预测就不准确了,但是比差棋手一步都走不好还是要好,所以还是能赢。)
MaxMin算法适用于对手很强大的前提下(Min)
2.2 ExpectiMax算法
ExpectiMax算法也是博弈算法的一种,它不像MinMax那样极端,认为对手一定会选最优,而是认为对手会按照一种分布去选择,但是自己一定会选最优(不然自己怎么赢)。同样的ExpectiMax也是预测未来的棋局,假设当前我有N种下法,那么每种下法通过通过遍历能够得到未来的棋局,然后看N种下法中,那种遍历后能够得到好棋局的概率大就选那种下法下棋。
还是选择上面的例子进行分析,同样遍历两步后得到棋局如下。
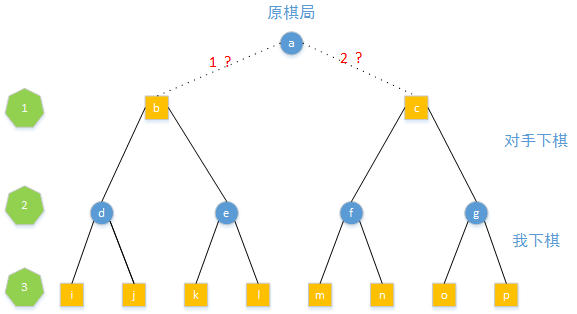
但是这里的对手的分布有所变化:
| 我的分布 | 选未来好棋局 | 选未来差棋局 |
|---|---|---|
| 概率 | 1 | 0 |
| 对手分布 | 选未来好棋局 | 选未来差棋局 |
|---|---|---|
| 概率 | 0.7 | 0.3 |
对第3步后的棋局进行评分:
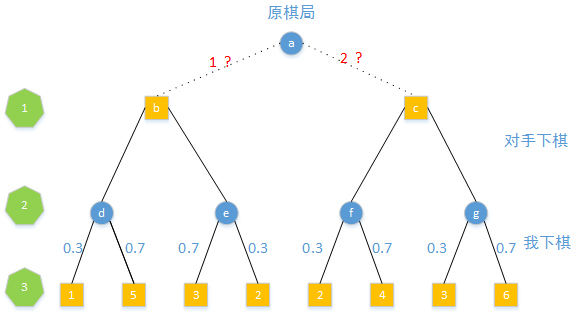
从d棋局出发得到1分棋局的概率为0.3,从d棋局出发得到5分的棋局的概率为0.7,那么d棋局未来得分的期望值为 10.3+50.7=3.8,同理可以得到e、f、g棋局的得分。
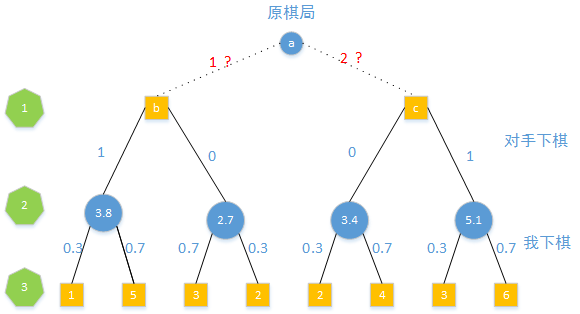
如果从b棋局出发,得到3.8分棋局的概率为1,所以b棋局未来得分的期望为3.8,同样的c棋局未来得分的期望为5.1
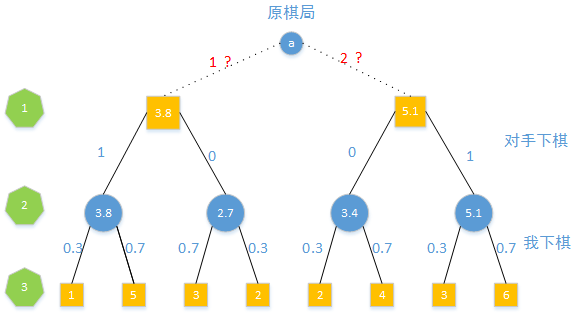
这个时候我们知道我们在a棋局下,选择1下法,未来棋局的期望值为3.8,选择2下法,未来棋局得分的期望值为5.1,当然我们会选择2下法。
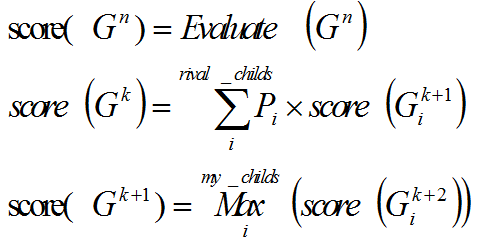
k和n表示预测的深度(第n步后直接使用evaluate的值),rival_childs表示对手$Gk$在棋局时能够得到的所以棋局$G{k+1}_i$,my_childs表示我在$G{k+1}$棋局值能够得到所以棋局。在对手局的时候,对手会根据一定的分布选择下一个棋局$G{k+2}_i$。在我的棋局时,我会选择最好的棋局。在计算期望的过程中选先要把棋局往下展开,并在第n步以后对棋局进行评估得到棋局的分数,然后往上计算棋局的期望,最后能得到初始棋局能到达的N个棋局的期望,取则N个棋局最后最好的棋局作为初始棋局的下一关棋局。
2048的对手不是智能的,而是一个按照一定分布随机放置一个块,所以使用expectimax算法比较合适。
除了求期望的算法,决定性能好坏的因素就是evaluate方式,对棋局评估的准确性能就好。在2048中评估的棋局好坏的因素有如下几个,通过这些方面然后乘上一个权重就能相对准确的描述棋局的好坏。
- 数据块的单调性 :monotonous
- 空格数:emptys
- 可合并数 :merges
3 CMA-ES算法
这里会遇到权重怎么设的问题,通常我们会自己根据结果手动调整,但是这种方式麻烦且不准确,不一定能选出好的权重值。
4 C++多线程处理及获取子线程的返回值
#include <iostream>
#include <cstdlib>
#include <pthread.h>
#include <unistd.h>
using namespace std;
#define NUM_THREADS 5
void *wait(void *t)
{
int i;
long tid;
tid = (long)t;
sleep(1);
cout << "Sleeping in thread " << endl;
cout << "Thread with id : " << tid << " ...exiting " << endl;
pthread_exit(NULL);
}
int main ()
{
int rc;
int i;
pthread_t threads[NUM_THREADS];
pthread_attr_t attr;
void *status;
// 初始化线程属性
pthread_attr_init(&attr);
// 设置线程为可连接的(joinable),如果为不可连接的就不能用join函数同步。
pthread_attr_setdetachstate(&attr, PTHREAD_CREATE_JOINABLE);
for( i=0; i < NUM_THREADS; i++ ){
cout << "main() : creating thread, " << i << endl;
rc = pthread_create(&threads[i], NULL, wait, (void *)&i );
if (rc){
cout << "Error:unable to create thread," << rc << endl;
exit(-1);
}
}
// 删除属性,释放空间
pthread_attr_destroy(&attr);
for( i=0; i < NUM_THREADS; i++ ){
// 等待子线程结束
rc = pthread_join(threads[i], &status);
if (rc){
cout << "Error:unable to join," << rc << endl;
exit(-1);
}
cout << "Main: completed thread id :" << i ;
cout << " exiting with status :" << status << endl;
}
cout << "Main: program exiting." << endl;
pthread_exit(NULL);
}
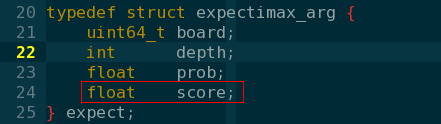
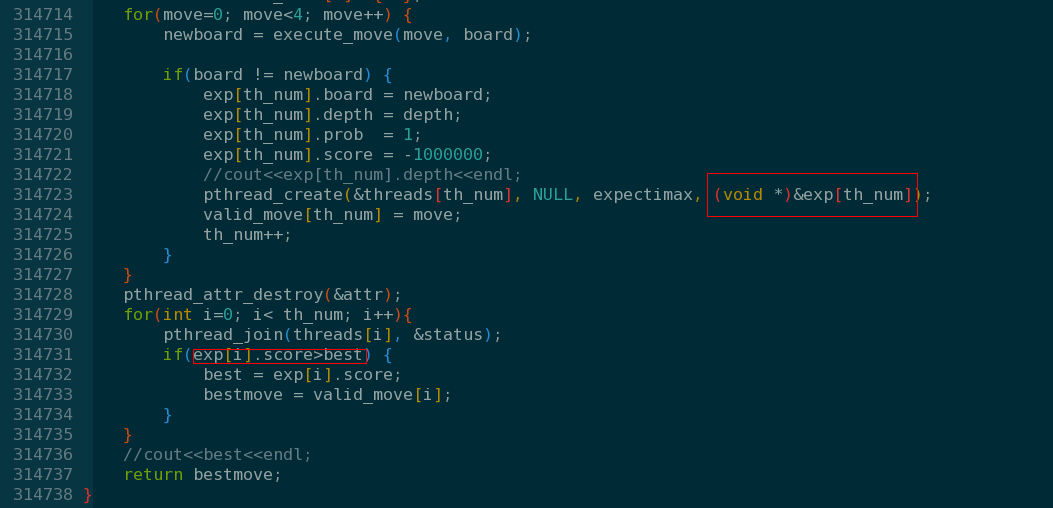
多线程返回参数是通过给子线程传一个结构体子针,子线程返回的时候结果保存在结构体的score域中。
5 python多进程并获取返回值
import multiprocessing
import time
def func(msg):
print multiprocessing.current_process().name + '-' + msg
if __name__ == "__main__":
pool = multiprocessing.Pool(processes=4) # 创建4个进程
for i in xrange(10):
msg = "hello %d" %(i)
pool.apply_async(func, (msg, ))
pool.close() # 关闭进程池,表示不能在往进程池中添加进程
pool.join() # 等待进程池中的所有进程执行完毕,必须在close()之后调用
print "Sub-process(es) done."
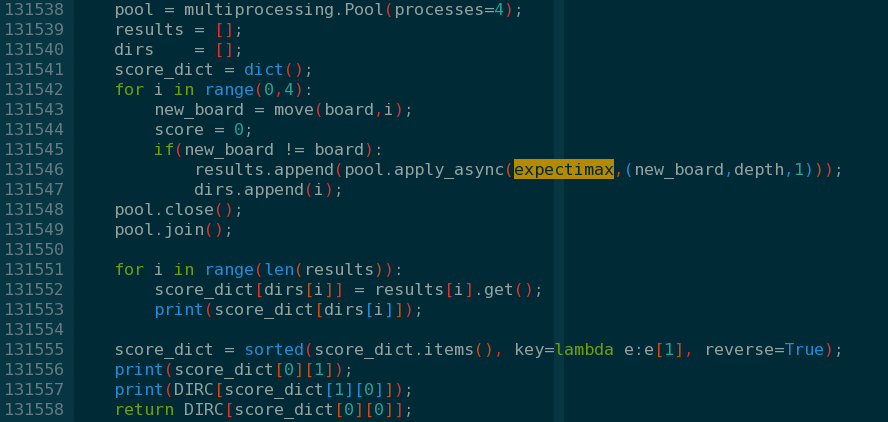
通过get()函数获取子线程的返回值。
7 python调用C/C++
- 在需要调用的函数上添加extern “C”
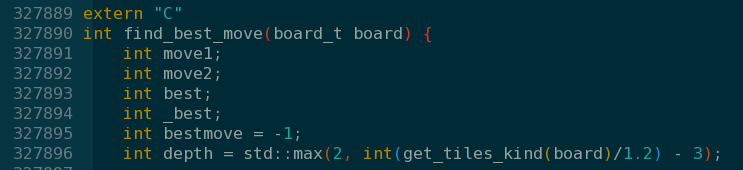
- 编译的时候需要添加 -fPIC -shared参数
g++ -fPIC -shared -lpthread -o 2048 2048.cpp

参考
- maxmin算法
- expectimax算法
- C++多线程处理及多线程获取子线程的返回值
-lpthread编译参数 - python的多进程处理及获取子进程的返回值
- python调用C/C++ (编译参数)
g++ -fPIC -shared -lpthread -o 2048 2048.cpp
原文写于2019-02-02,2021-12-07改为markdown