图是一种比线性表和树更为复杂的数据结构,在图结构中,结点之间的关系可以是任意的,图中任意两个数据元素之间都可能相关。
列举图的基本术语:子图;无向完全图,有向完全图;稀疏图,稠密图;权,网;邻接点;度,入度,出度;路径,路径长度;回路,环;简单路径,简单回路,简单环;联通,连通图,连通分量;强连通图,强连通分量;连通图的生成树;有向树,生成森林。
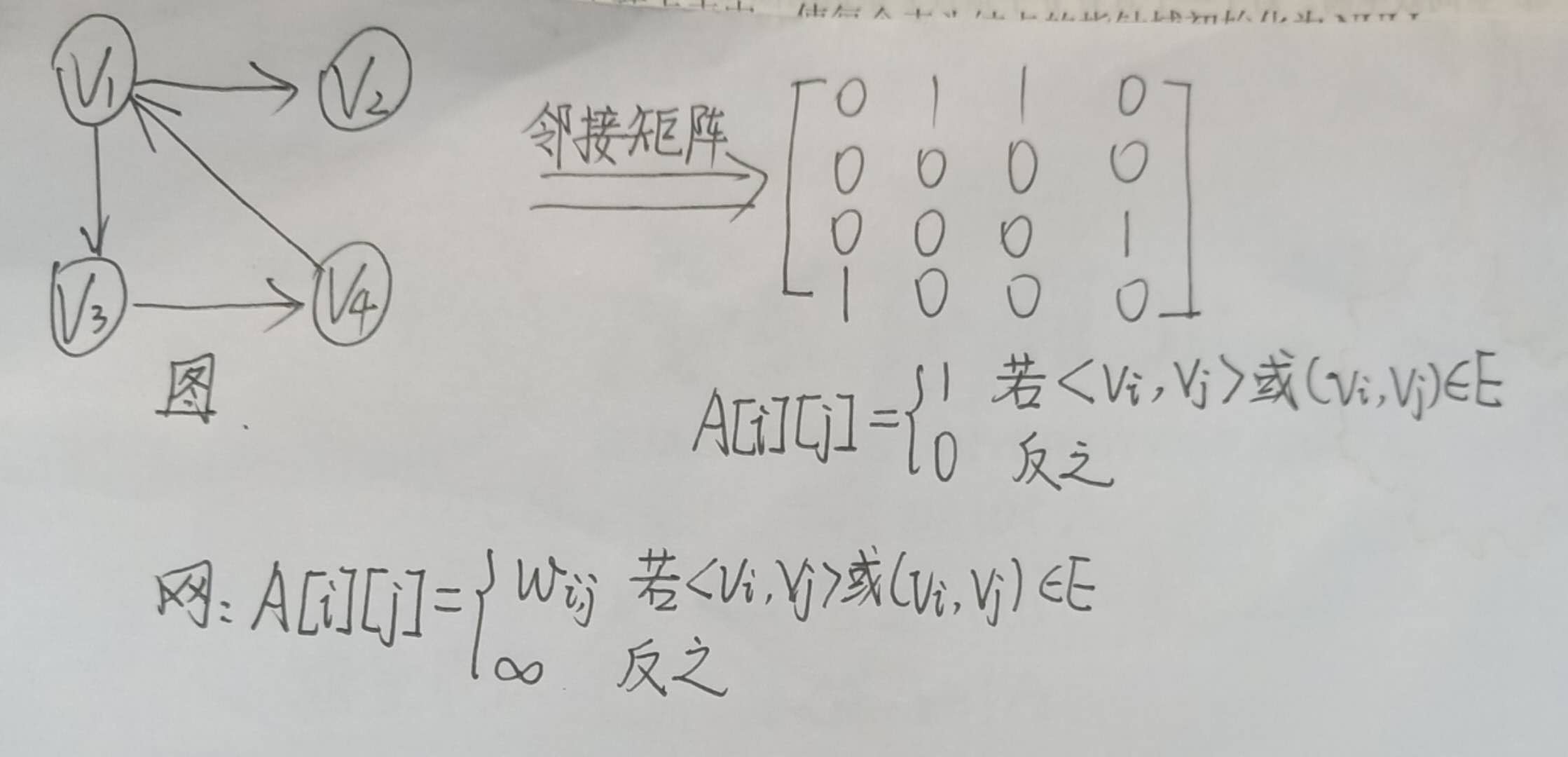
、图的存储结构
①邻接矩阵

//—————图的邻接矩阵存储表示 #define MaxInt 32767 //表示极大值,即∞ #define MVNum 100 //最大顶点数 typedef char VerTexType; //假设顶点的数据类型为字符型 typedef int ArcType; //假设边的权值类型为整型 typedef struct { VerTexType vexs[MVNum]; //顶点表 ArcType arcs[MVNum][MVNum]; //邻接矩阵 int vexnum, arcnum; //图的当前点数和边数 }AMGraph; Status CreateUDN(AMGraph &G) { cin >> G.vexnum >> G.arcnum; //输入总顶点数、总边数 for(i=0; i<G.vexnum; ++i) //依次输入点的信息 cin >> G.vexs[i]; for(i=0; i<G.vexnum; ++i) //初始化邻接矩阵,边的权值均置为MaxInt for(j=0; j<G.vexnum; ++j) G.arcs[i][j] = MaxInt; for(k=0; k<G.arcnum; ++k) { cin >> v1 >> v2 >> w; i = LocateVex(G, v1); j = LocateVex(G, v2); G.arcs[i][j] = w; G.arcs[j][i] = G.arcs[i][j]; } return OK; }
②邻接表
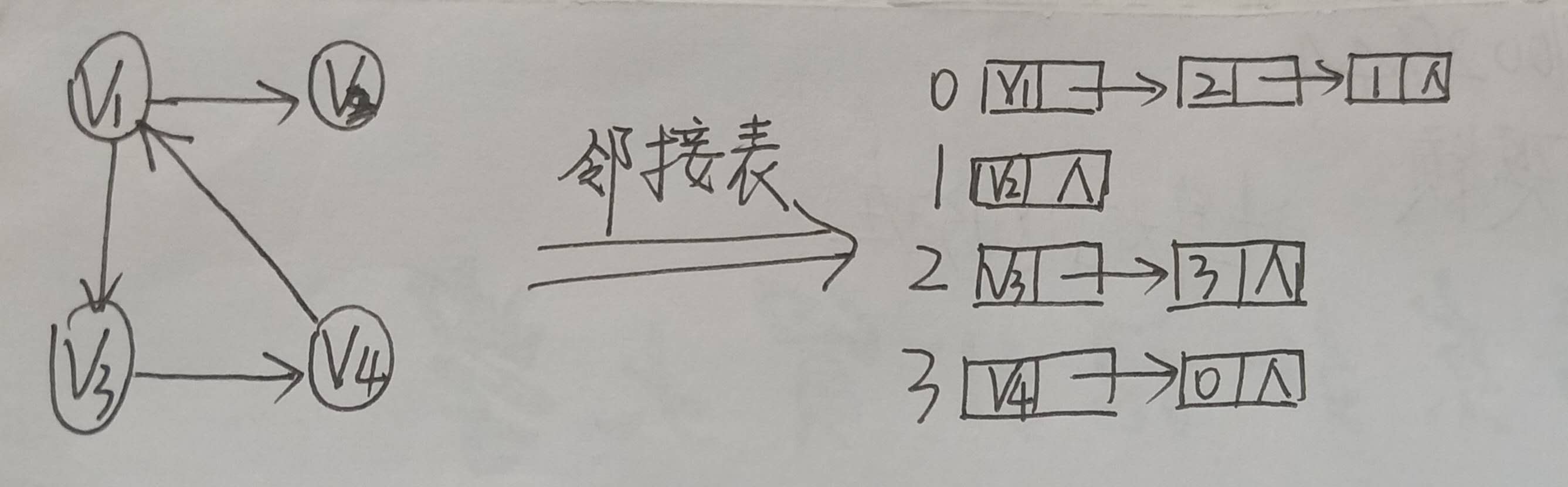

//————图的邻接表存储表示 #define MVNum 100 //最大顶点数 typedef struct ArcNode //边结点 { int adjvex; //该边所指向的顶点的位置 struct ArcNode *nextarc; //指向下一条边的指针 OtherInfo info; //和边相关的信息 }ArcNode; typedef struct VNode //顶点信息 { VerTexType data; ArcNode *firstarc; //指向第一条依附该顶点的边的指针 }VNode, AdjList[MVNum]; //AdjList 表示邻接表类型 typedef struct //邻接表 { AdjList vertices; int vexnum. arcnum; //图的当前顶点数和边数 }ALGraph;

Status CreateUDG (ALGraph &G) { cin >> G.vexnum >> G.arcnum; //输入总顶点数,总边数 for(i=0; i<G.vexnum; ++i) //输入各点,构造表头结点表 { cin >> G.vertices[i].data; //输入顶点值 G.vertices[i].firstarc = NULL; //初始化表头结点的指针域为NULL }//for for(k=0; k<G.arcnum; ++k) //输入各边,构造邻接表 { cin >> v1 >> v2; //输入一条边依附的两个顶点 i = LocateVex(G,v1); j = LocateVex(G,v2); //确定v1和v2在G中的位置,即顶点在G.vertices中的序号 p1 = new ArcNode; //生成一个新的边结点*p1 p1->adjvex = j; p1->nextarc = G.vertices[i].firstarc; G.vertices[i].firstarc = p1; //将新结点*p1插入顶点vi的边表头部 p2 = new ArcNode; //生成另一个对称的新的边结点*p2 p2->adjvex = i; //邻接点序号为i p2->nextarc = G.vertices[j].firstarc; G.vertices[j].firstarc = p2; //将结点*p2插入顶点vj的边表头部 }//for return OK; }
、(连通)图的遍历
①深度优先搜索 DFS
类似于树的先序遍历过程

bool visited[MVNum]; //访问标志数值,其初值为"false" void DFS(Graph G, int v) {//从第v个顶点出发递归地深度优先遍历图G cout << v; //访问第v个顶点,并置访问标志数组相应分量值为true visited[v] = true; for(w=FirstAdjVex(G,v); w>=0; w=NextAdjVex(G,v,w)) //依次检查v的所有邻接点w,FirstAdjVex表示v的第一个邻接点 //NextAdjVex(G,v,w)表示v相对于w的下一个邻接点,w≧0表示存在邻接点 if(!visited[w]) DFS(G,w); //对v的尚未访问顶点w递归调用DFS }

void DFS_AM(AMGraph G, int v) { cout << v; visited[v] = true; for(w=0; w<G.vexnum; w++) if((G.arcs[v][w]!=0)&&(!visited[w])) DFS_AM(G,w); }

void DFS_AL(ALGraph G, int v) { cout << v; visited[v] = true; p = G.vertices[v].firstarcs; while(p!=NULL) { w = p->adjvex; if(!visited[w]) DFS_AL(G,w); p = p->nextarc; } }
②广度优先搜索 BFS
类似于树的按层次遍历过程

void BFS(Graph G, int v) { cout << v; visited[v] = true; InitQueue(Q); //辅助队列初始化,置空 EnQueue(Q,v) //v进队 while(!QueueEmpty(Q)) { DeQueue(Q,u); //对头元素出队并置为u for(w=FirstAdjVex(G,u); w>=0; w=NextAdjVex(G,u,w)) if(!visited[w]) { cout << w; visited[w] = true; EnQueue(Q,w); //w进队 } } } BFS的算法
老师的强调::弄清楚所使用的辅助数据结构的初始态、过程态、终态。
、图的应用
1、最小生成树
利用MST性质
①归并点:普里姆算法(Prim)
②归并边:克鲁斯卡尔算法(Kruskal)
2、最短路径
①从某个源点到其余各顶点的最短路径
迪杰斯特拉算法
②每一对顶点之间的最短路径
弗洛伊德算法
3、拓扑排序
4、关键路径
