20172313 2018-2019-1 《程序设计与数据结构》实验三报告
课程:《程序设计与数据结构》
班级: 1723
姓名: 余坤澎
学号:20172313
实验教师:王志强
实验日期:2018年11月20日
必修/选修: 必修
1.实验内容
- 实验一 定义一个Searching和Sorting类,并在类中实现linearSearch(教材P162 ),SelectionSort方法(P169),最后完成测试。要求不少于10个测试用例,提交测试用例设计情况(正常,异常,边界,正序,逆序),用例数据中要包含自己学号的后四位提交运行结果图。
- 实验二 重构你的代码把Sorting.java Searching.java放入 cn.edu.besti.cs1723.(姓名首字母+四位学号) 包中(例如:cn.edu.besti.cs1723.G2301)把测试代码放test包中
重新编译,运行代码,提交编译,运行的截图(IDEA,命令行两种) - 实验三 参考http://www.cnblogs.com/maybe2030/p/4715035.html 在Searching中补充查找算法并测试提交运行结果截图
- 实验四 补充实现课上讲过的排序方法:希尔排序,堆排序,二叉树排序等(至少3个)测试实现的算法(正常,异常,边界)。提交运行结果截图
- 实验五 编写Android程序对各种查找与排序算法进行测试,提交运行结果截图,推送代码到码云。
2. 实验过程及结果
实验一
- 实验一大体上来说没有什么难度,相应的代码在之前也有练习过,实验一主要是用来复习Junit测试,在进行Junit测试的时候要注意测试用例的设计,要囊括各种情况:正常、异常、边界、正序、逆序。以确保代码的正确性。
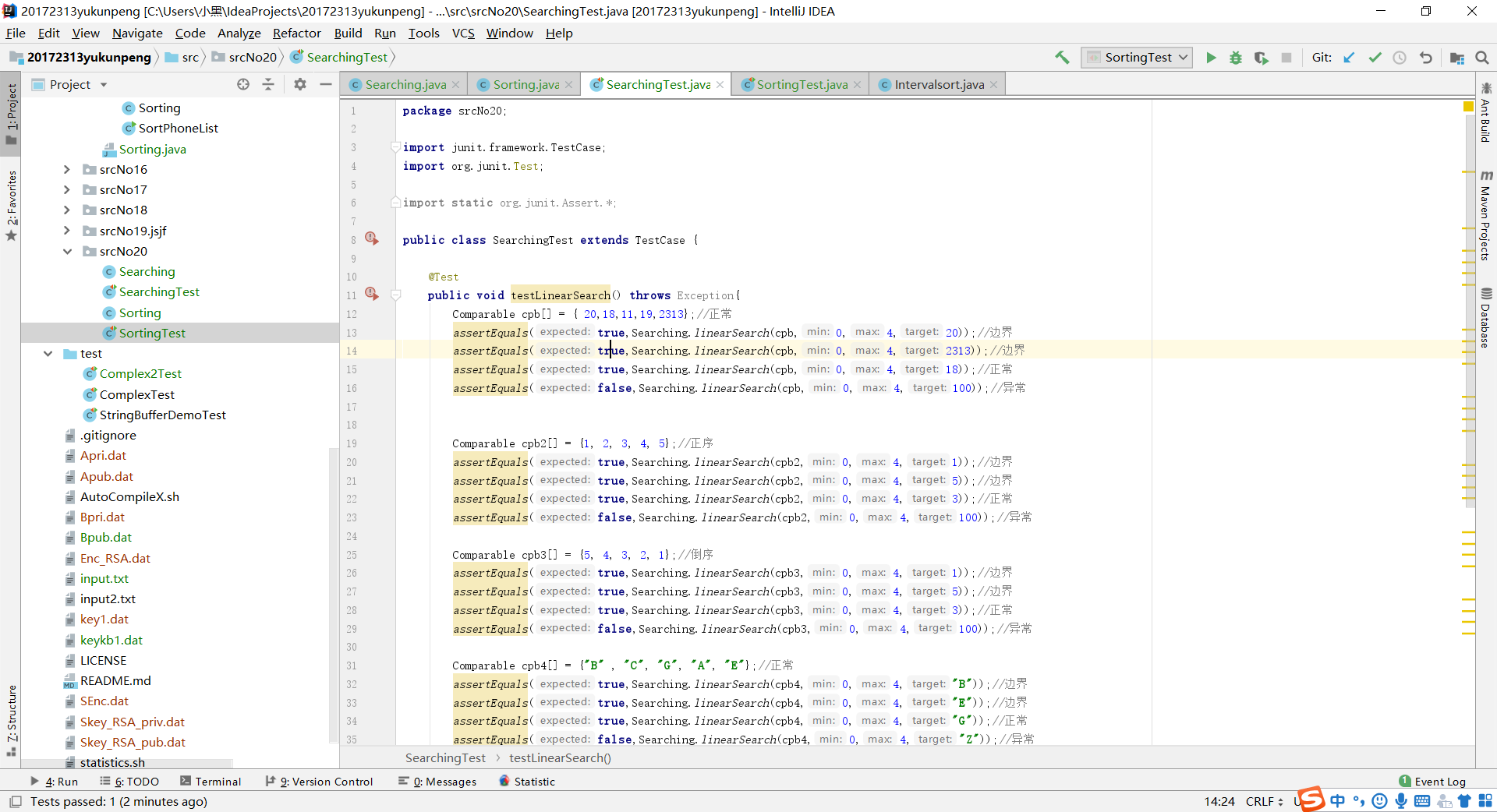
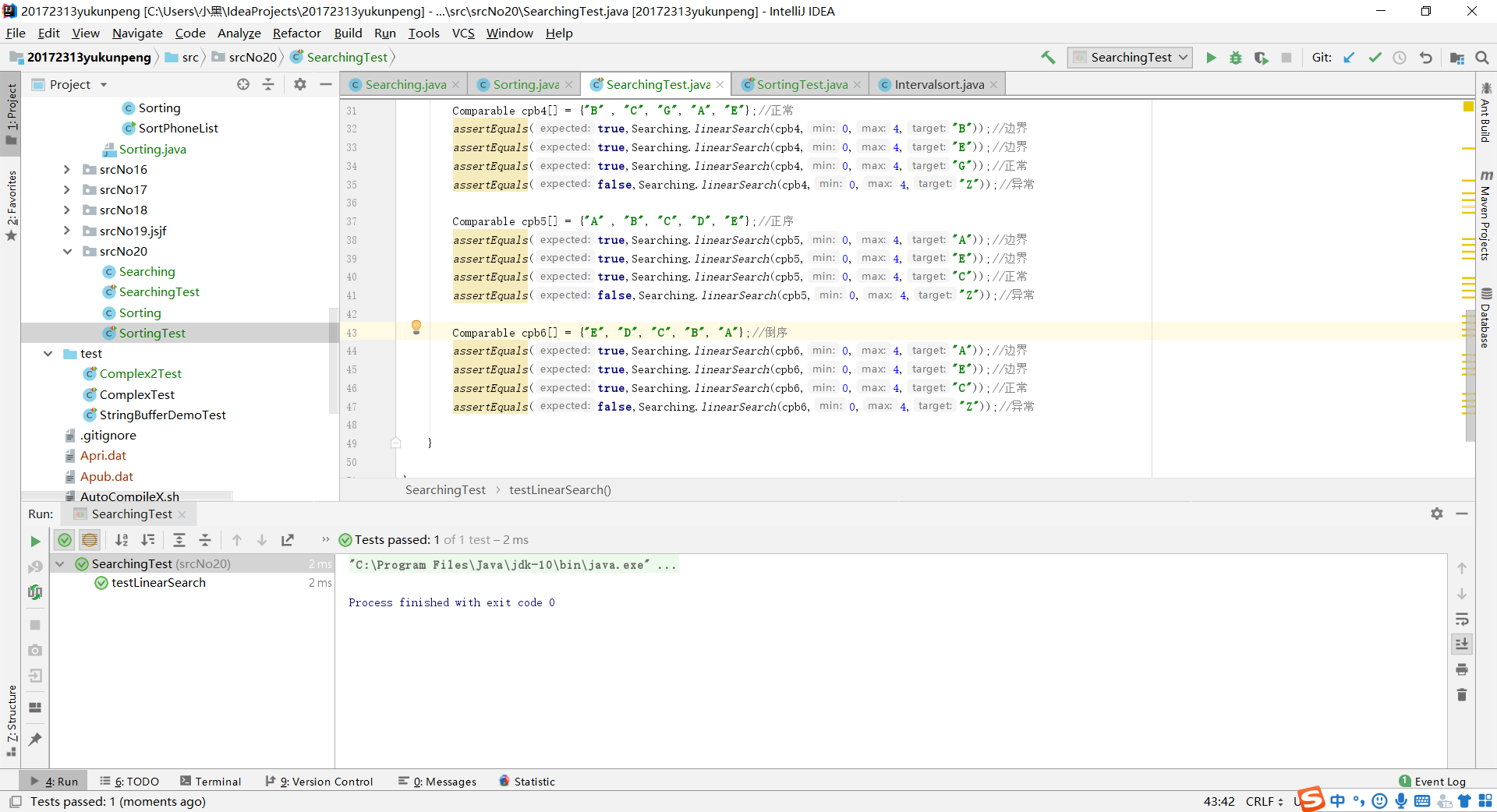
实验二
- 实验二重构代码只是将代码放到其他的包中,在IDEA下运行只需要简单的拖拉,复制粘贴即可完成,在命令行下实现花了一番功夫,太久没有在Linux下进行代码的编写,指令也有些忘记,复习了Linux的操作后,实验二也就OK了!

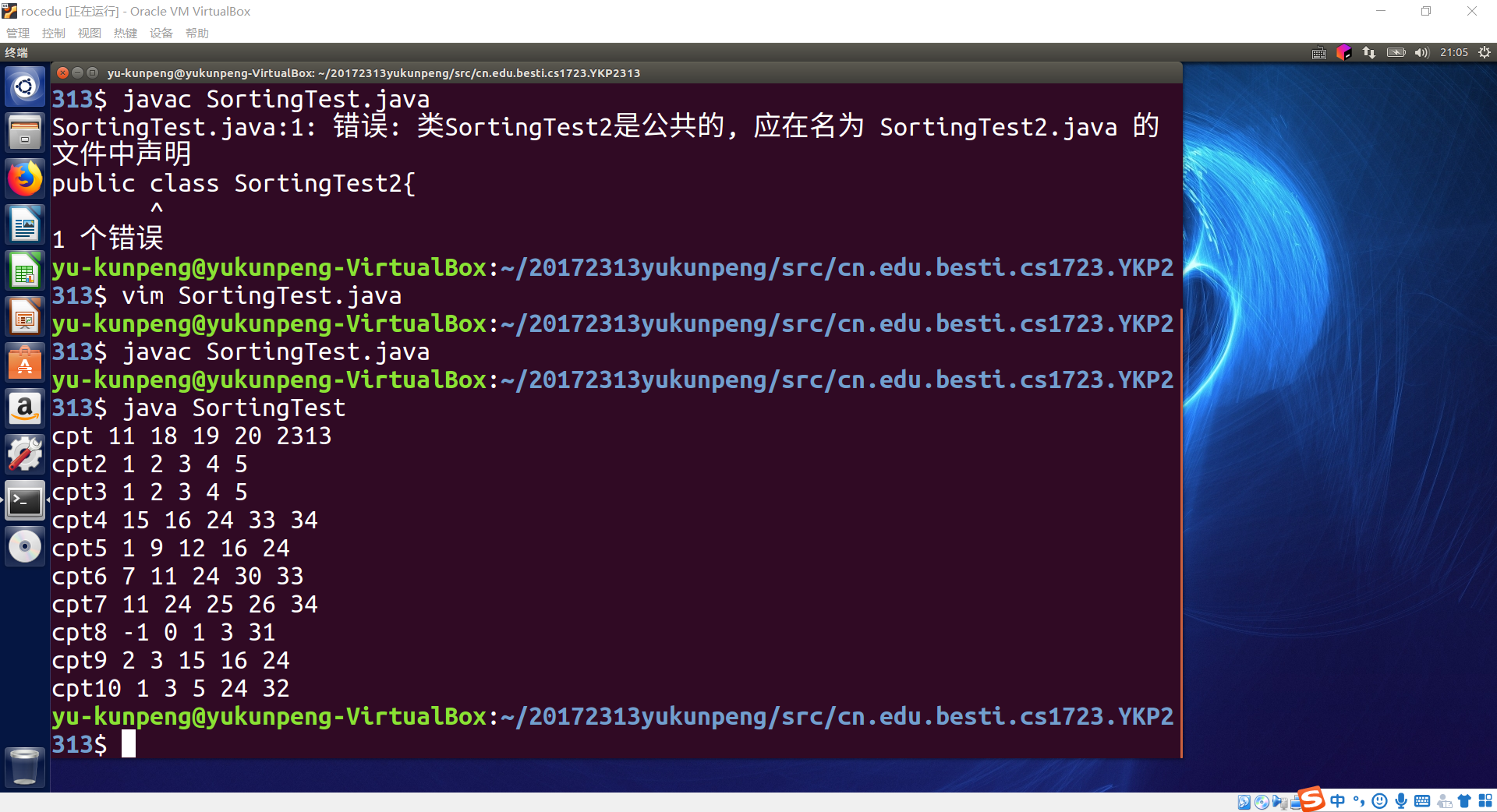
实验三
- 实验三的难度有所增加,其他的查找算法之前也有写过,这里主要是斐波那契查找比较陌生,这种查找的精髓在于采用最接近查找长度的斐波那契数值来确定拆分点,也就是利用到了黄金比例。详细的代码分析和理解在下文的实验问题中将会提到。
//斐波那契查找
public int fbSearch(int[] array, int a) {
if (array == null || array.length == 0) {
return -1;
} else {
int length = array.length;
int[] fb = makeFbArray(length + 2);
int k = 0;
while (length > fb[k] - 1) {// 找出数组的长度在斐波数列(减1)中的位置,将决定如何拆分
k++;
}
int[] temp = Arrays.copyOf(array, fb[k] - 1);
for (int i = length; i < temp.length; i++) {
if (i >= length) {
temp[i] = array[length - 1];
}
}
int low = 0;
int hight = array.length - 1;
while (low <= hight) {
int middle = low + fb[k - 1] - 1;
if (temp[middle] > a) {
hight = middle - 1;
k = k - 1;
} else if (temp[middle] < a) {
low = middle + 1;
k = k - 2;
} else {
if (middle <= hight) {
return middle;// 此时mid即为查找到的位置
} else {
return hight;// 此时middle的值已经大于hight,进入扩展数组的填充部分,即最后一个数就是要查找的数。
}
}
}
return -1;
}
}
//生成一个指定长度的斐波数列
public int[] makeFbArray(int length) {
int[] array = null;
if (length > 2) {
array = new int[length];
array[0] = 1;
array[1] = 1;
for (int i = 2; i < length; i++) {
array[i] = array[i - 1] + array[i - 2];
}
}
return array;
}
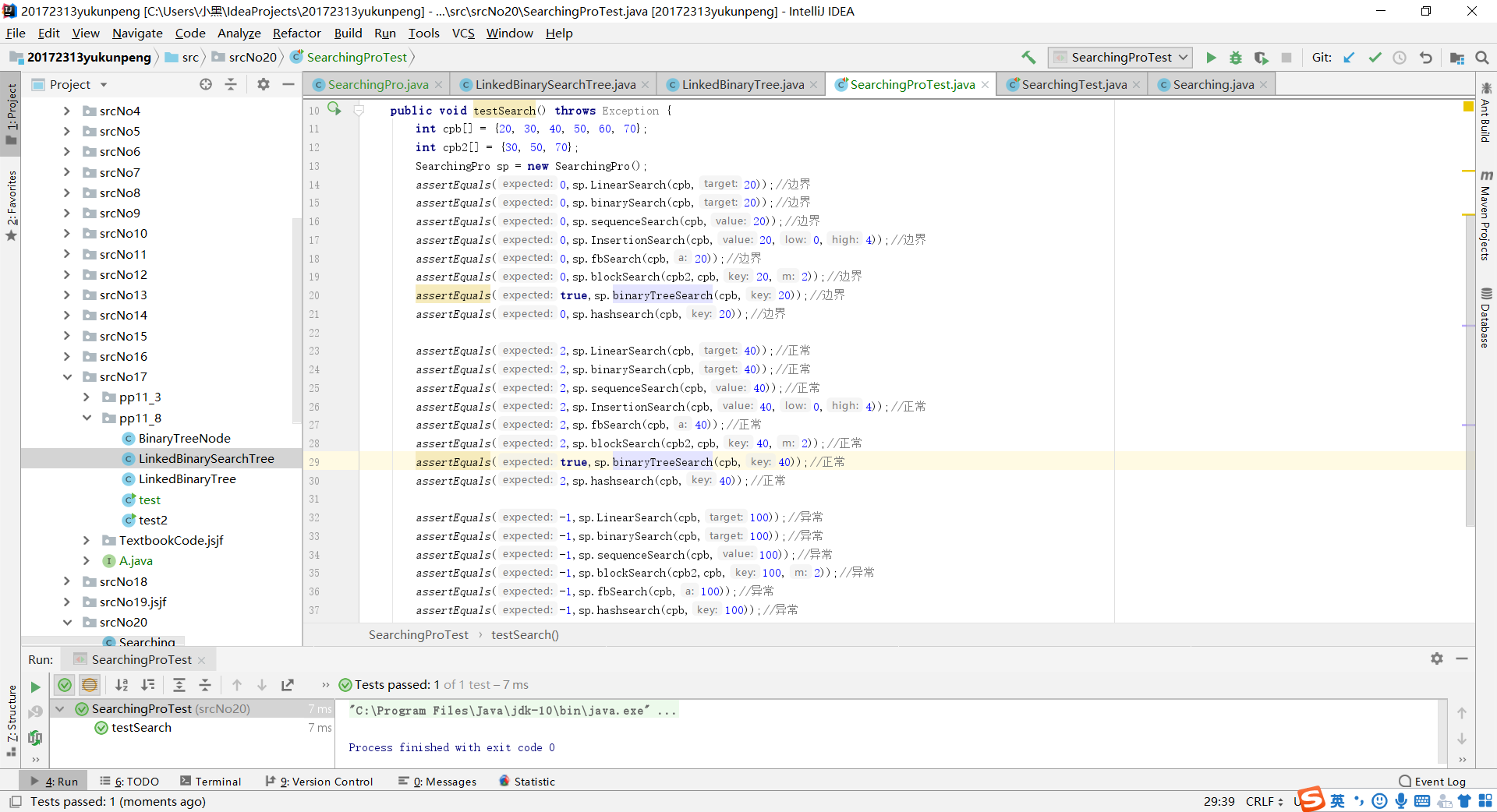
实验四
- 实验四要求实现补充课上所讲的排序方法,我在这里的主要思路就是每次找到最小值依次进行输出,最后得到排序好的结果。实验四也就完成了。
实验五
- 要求使用android studio进行测试,因为期末作业的缘故,所以对android studio的操作也进行了复习,所以在代码从IDEA移植到android studio并设计了图形界面没什么困难和问题。
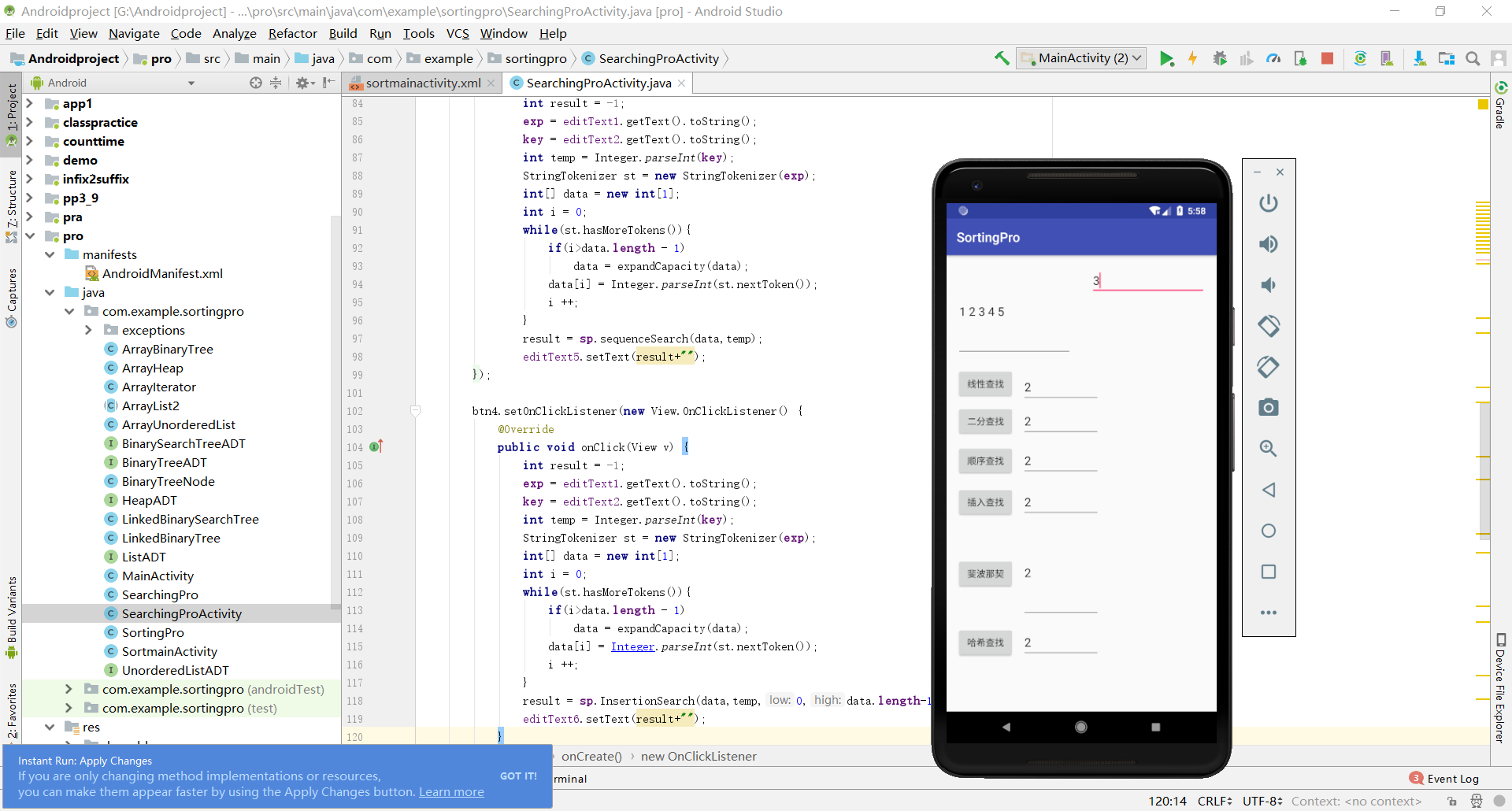
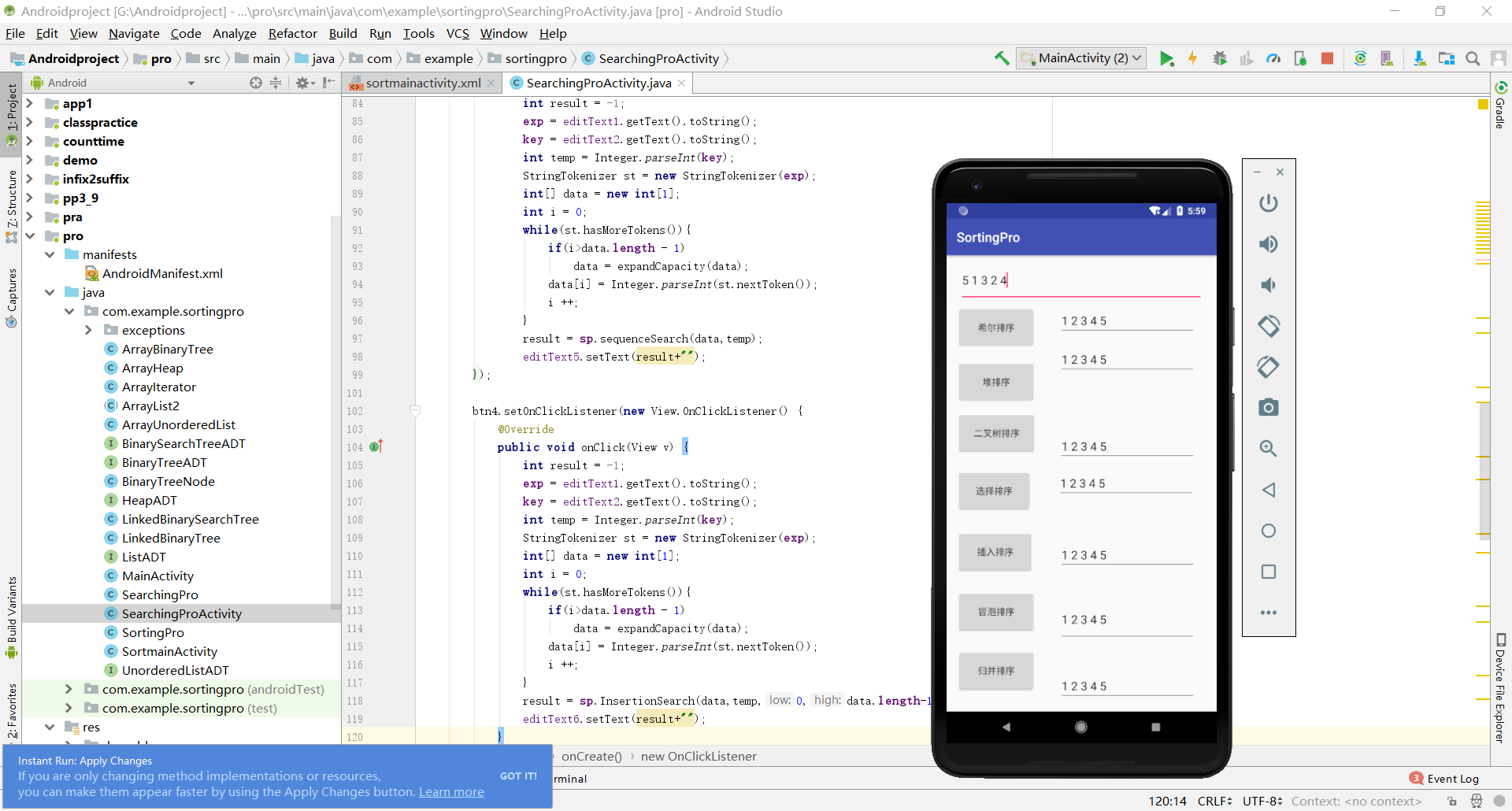
实验过程中遇到的问题和解决过程
- 问题一:在做实验三的时候对斐波那契查找比较陌生,不是非常明白他的具体操作步骤。
- 问题一解决方案:既然是斐波那契查找法,我们首先需要知道斐波那契数列究竟是什么。
斐波那契数列(Fibonacci sequence),又称黄金分割数列、因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波纳契数列以如下被以递归的方法定义:F(0)=1,F(1)=1, F(n)=F(n-1)+F(n-2)(n>=2,n∈N*)
通俗的来讲,就是从第3个数开始,每一个数都等于它前面的两个数的和,而斐波那契查找则正是利用了它的性质,前一个数除以相邻的后一个数,比值无限接近黄金分割。现在假设我们有这样一个数列,它的长度为9(数值任意),则它对应的斐波那契数列为{1,1,2,3,5,8,13,21,34}(长度要大于等于9),大于9且最接近9的斐波那契数值是f[6]=13,为了满足所谓的黄金分割,所以它的第一个拆分点应该就是f[6]的前一个值f[5]=8,即待查找数组array的第8个数,对应到下标就是array[7],依次类推。推演到一般情况,假设有待查找数组array[n]和斐波那契数组F[k],并且n满足n>=F[k]-1&&n < F[k+1]-1,则它的第一个拆分点middle=F[k]-1。如果n刚好等于F[k]-1,待查找数组刚好拆成F[k-1]和F[k-2]两部分;然而大多数情况并不能尽人意,n会小于F[k]-1,这时候我们需要使用补齐,用最大的数来填充F[k-2]的残缺部分,如果查找的位置落到补齐的部分,那就可以确定要找的那个数就是最后一个最大的了。
其他
这次实验总体上来说难度不大,很多都是之前联系过的内容,在这次实验中主要是复习了Juni测试,命令行使用以及androidstudio的使用。在这次实验中还是发现了自己的不足,没有对以往的内容进行很好的复习。希望在这次认识到自己的不足后能够加以改正,在以后的学习生活中继续进步。